江苏省南京雨花台区七校联考2022-2023学年七下数学期末学业质量监测模拟试题含答案

江苏省南京雨花台区七校联考2022-2023学年七下数学期末学业质量监测模拟试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项

1．考生要认真填写考场号和座位序号。

2．试题所有答案必须填涂或书写在答题卡上，在试卷上作答无效。第一部分必须用2B 铅笔作答；第二部分必须用黑色字迹的签字笔作答。

3．考试结束后，考生须将试卷和答题卡放在桌面上，待监考员收回。

一、选择题(每小题3分,共30分)

1．下列代数式变形正确的是（　　）

A． B．

C． D．

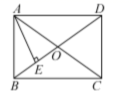
2．如图，在矩形中，对角线、相交于点，垂直平分，若cm，则（）

A． B． C． D．

3．有11名同学参加100米赛跑，预赛成绩各不相同，要取前6名参加决赛，小明已经知道了自己的成绩，他想知道自己能否进入决赛，还需要知道这11名同学成绩的（    ）

A．中位数 B．平均数 C．众数 D．方差

4．下列式子中为最简二次根式的是（　　）

A． B． C． D．

5．如果一个正多边形的内角和是这个正多边形外角和的2倍，那么这个正多边形是(　　)

A．等边三角形 B．正四边形 C．正六边形 D．正八边形

6．若点P到△ABC的三个顶点的距离相等，则点P是△ABC（　　　　）

A．三条高的交点 B．三条角平分线的交点

C．三边的垂直平分线的交点 D．三条中线的交点

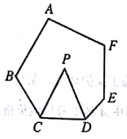
7．如图，在六边形中，，分别平分，则的度数为（   ）

A． B． C． D．

8．某校八年级(3)班体训队员的身高(单位：cm)如下：169，165，166，164，169，167，166，169，166，165，获得这组数据方法是(   )

A．直接观察 B．查阅文献资料 C．互联网查询 D．测量

9．某新品种葡萄试验基地种植了10亩新品种葡萄，为了解这些新品种葡萄的单株产量，从中随机抽查了4株葡萄，在这个统计工作中，4株葡萄的产量是(    )

A．总体    B．总体中的一个样本    C．样本容量    D．个体

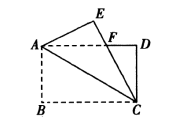
10．如图，矩形纸片中，，将沿折叠，使点落在点处，交于点，则的长等于(    )

A． B． C． D．

二、填空题(本大题共有6小题，每小题3分，共18分)

11．函数向右平移1个单位的解析式为__________．

12．如果关于的方程有实数解，那么的取值范围是_________.

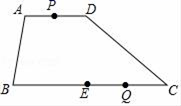
13．如图，在四边形ABCD中，AD∥BC，AD=4，BC=12，点E是BC的中点．点P、Q分别是边AD、BC上的两点，其中点P以每秒个1单位长度的速度从点A运动到点D后再返回点A，同时点Q以每秒2个单位长度的速度从点C出发向点B运动．当其中一点到达终点时停止运动．当运动时间t为_____秒时，以点A、P，Q，E为顶点的四边形是平行四边形．

14．将直线平移后经过点（5，），则平移后的直线解析式为______________．

15．若关于x的一元二次方程x22x+m＝0有实数根，则实数m的取值范围是______ ．

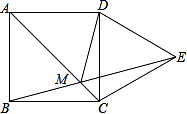
16．如图，四边形ABCD是正方形，以CD为边作等边三角形CDE，BE与AC相交于点M，则∠ADM的度数是_____．

三、解下列各题(本大题共8小题，共72分)

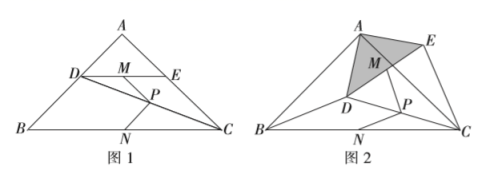
17．（8分）定义：既相等又垂直的两条线段称为“等垂线段”，如图1，在中，，，点、分别在边、上，，连接、，点、、分别为、、的中点，且连接、．

观察猜想

（1）线段与         “等垂线段”（填“是”或“不是”）

猜想论证

（2）绕点按逆时针方向旋转到图2所示的位置，连接，，试判断与是否为“等垂线段”，并说明理由．

拓展延伸

（3）把绕点在平面内自由旋转，若，，请直接写出与的积的最大值．

18．（8分）在平面直角坐标系中，已知点A（﹣4，2），B（﹣4，0），C（﹣1，1），请在图上画出△ABC，并画出与△ABC关于原点O对称的图形．

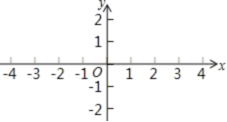
19．（8分）计算:(1)÷-×+ ；(2)(-1)101+(π-3)0+-.

20．（8分）如图，在菱形ABCD中，CE⊥AB交AB延长线于点E，点F为点B关于CE的对称点，连接CF，分别延长DC，CF至点G，H，使FH=CG，连接AG，DH交于点P．

（1）依题意补全图1；

（2）猜想AG和DH的数量关系并证明；

（3）若∠DAB=70°，是否存在点G，使得△ADP为等边三角形？若存在，求出CG的长；若不存在，说明理由．

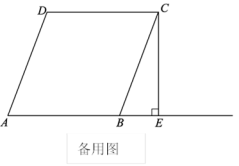
21．（8分）如图，点在等边三角形的边，延长至，使，连接交于.

求证：.

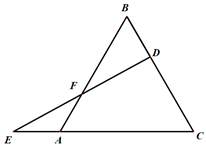
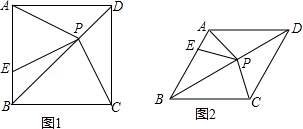
22．（10分）如图1，在正方形ABCD中，P是对角线BD上的点，点E在AB上，且PA=PE．

（1）求证：PC=PE；

（2）求∠CPE的度数；

（3）如图2，把正方形ABCD改为菱形ABCD，其他条件不变，试探究∠CPE与∠ABC之间的数量关系，并说明理由．

23．（10分）已知，在菱形ABCD中，G是射线BC上的一动点（不与点B，C重合），连接AG，点E、F是AG上两点，连接DE，BF，且知∠ABF=∠AGB，∠AED=∠ABC．

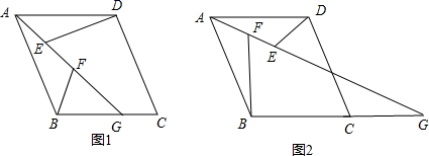
（1）若点G在边BC上，如图1，则：

①△ADE与△BAF______；（填“全等”或“不全等”或“不一定全等”）

②线段DE、BF、EF之间的数量关系是______；

（2）若点G在边BC的延长线上，如图2，那么上面（1）②探究的结论还成立吗？如果成立，请给出证明；如果不成立，请说明这三条线段之间又怎样的数量关系，并给出你的证明．

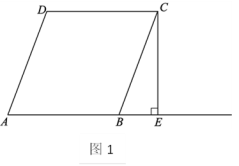
24．（12分）古埃及人用下面的方法得到直角三角形，把一根长绳打上等距离的13个结（12段），然后用桩钉钉成一个三角形，如图1，其中∠C便是直角．

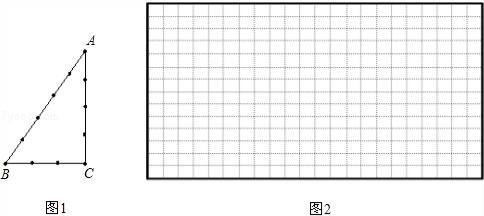
（1）请你选择古埃及人得到直角三角形这种方法的理由　   　（填A或B）

A．勾股定理：在直角三角形边的两直角边的平方和等于斜边的平方

B．勾股定理逆定理：如果三角形的三边长a、b、c有关系：a2+b2＝c2，那么这个三角形是直角三角形

（2）如果三个正整数a、b、c满足a2+b2＝c2，那么我们就称 a、b、c是一组勾股数，请你写出一组勾股数　   　

（3）仿照上面的方法，再结合上面你写出的勾股数，你能否只用绳子，设计一种不同于上面的方法得到一个直角三角形（在图2中，只需画出示意图．）

参考答案

一、选择题(每小题3分,共30分)

1、D

2、C

3、A

4、C

5、C

6、C

7、A

8、D

9、B

10、B

二、填空题(本大题共有6小题，每小题3分，共18分)

11、或

12、

13、2或.

14、y=2x-1

15、m≤1

16、75°

三、解下列各题(本大题共8小题，共72分)

17、（1）是；（2）是，理由详见解析；（3）49

18、见解析

19、（1） （2）

20、 (1)见解析;(2) AG=DH,理由见解析;(3) 不存在．理由见解析.

21、证明见解析.

22、（1）见解析；（2）∠EPC=90°；（3）∠ABC+∠EPC=180°．

23、（1）①全等；②DE=BF+EF；（2）DE=BF-EF，见解析

24、（1）B（2）（6，8，10）（3）见解析