


广州大附属中学2022-2023学年数学七年级第二学期期末检测模拟试题含答案
展开广州大附属中学2022-2023学年数学七年级第二学期期末检测模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
考生须知:
1.全卷分选择题和非选择题两部分,全部在答题纸上作答。选择题必须用2B铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。
2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。
3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。
一、选择题(每小题3分,共30分)
1.如图,MN是正方形ABCD的一条对称轴,点P是直线MN上的一个动点,当PC+PD最小时,∠PCD=( )
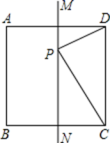
A.60° B.45° C.30° D.15°
2.如图,在任意四边形ABCD中,M,N,P,Q分别是AB,BC,CD,DA上的点,对于四边形MNPQ的形状,以下结论中,错误的是![]()
![]()
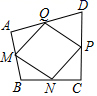
A.当M,N,P,Q是各边中点,四边MNPQ一定为平行四边形
B.当M,N,P,Q是各边中点,且![]() 时,四边形MNPQ为正方形
时,四边形MNPQ为正方形
C.当M,N、P,Q是各边中点,且![]() 时,四边形MNPQ为菱形
时,四边形MNPQ为菱形
D.当M,N、P、Q是各边中点,且![]() 时,四边形MNPQ为矩形
时,四边形MNPQ为矩形
3.如图,在平面直角坐标系中,▱MNEF的两条对角线ME,NF交于原点O,点F的坐标是(3,2),则点N的坐标为( )
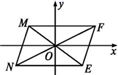
A.(-3,-2) B.(-3,2) C.(-2,3) D.(2,3)
4.式子![]() 在实数范围内有意义,则
在实数范围内有意义,则![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.根据下表中一次函数的自变量x与函数y的对应值,可得p的值为()
x | -2 | 0 | 1 |
y | 3 | p | 0 |
A.1 B.-1 C.3 D.-3
6.如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,已知AE=6,![]() ,则EC的长是( )
,则EC的长是( )
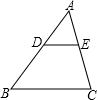
A.4.5 B.8 C.10.5 D.14
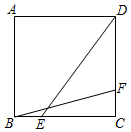
7.如图,在边长为4的正方形ABCD中,点E、F分别是边BC、CD上的动点.且BE=CF,连接BF、DE,则BF+DE的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.设三角形的三边长分别等于下列各组数,能构成直角三角形的是( )
A.![]() ,
, ![]() ,
,![]()
![]() B.
B.![]() ,
,![]() ,
,![]()
![]() C.
C.![]() ,
,![]() ,
,![]()
![]() D.4,5,6
D.4,5,6
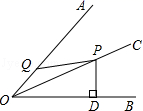
9.如图,OC平分∠AOB,点P是射线OC上的一点,PD⊥OB于点D,且PD=3,动点Q在射线OA上运动,则线段PQ的长度不可能是( )
A.2 B.3 C.4 D.5
10.在平面直角坐标系中,点(4,﹣3)关于y轴对称的点的坐标是( )
A.(﹣4,﹣3) B.(4,3) C.(﹣4,3) D.(4,﹣3)
二、填空题(本大题共有6小题,每小题3分,共18分)
11.分式方程![]() 有增根,则
有增根,则![]() 的值为__________。
的值为__________。
12.某个“清凉小屋”自动售货机出售![]() 三种饮料.
三种饮料.![]() 三种饮料的单价分别是2元/瓶、3元/瓶、5元/瓶. 工作日期间,每天上货量是固定的,且能全部售出,其中,
三种饮料的单价分别是2元/瓶、3元/瓶、5元/瓶. 工作日期间,每天上货量是固定的,且能全部售出,其中,![]() 饮料的数量(单位:瓶)是
饮料的数量(单位:瓶)是![]() 饮料数量的2倍,
饮料数量的2倍,![]() 饮料的数量(单位:瓶)是
饮料的数量(单位:瓶)是![]() 饮料数量的2倍. 某个周六,
饮料数量的2倍. 某个周六,![]() 三种饮料的上货量分别比一个工作日的上货量增加了50%,60%,50%,且全部售出. 但是由于软件bug,发生了一起错单(即消费者按某种饮料1瓶的价格投币,但是取得了另一种饮料1瓶),结果这个周六的销售收入比一个工作日的销售收入多了403元. 则这个“清凉小屋”自动售货机一个工作日的销售收入是__________元.
三种饮料的上货量分别比一个工作日的上货量增加了50%,60%,50%,且全部售出. 但是由于软件bug,发生了一起错单(即消费者按某种饮料1瓶的价格投币,但是取得了另一种饮料1瓶),结果这个周六的销售收入比一个工作日的销售收入多了403元. 则这个“清凉小屋”自动售货机一个工作日的销售收入是__________元.
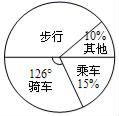
13.如图,某校根据学生上学方式的一次抽样调查结果,绘制出一个未完成的扇形统计图,若该校共有学生1500人,则据此估计步行的有_____.
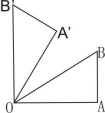
14.如图,∠A=90°,∠AOB=30°,AB=2,△![]() 可以看作由△AOB绕点O逆时针旋转60°得到的,则点
可以看作由△AOB绕点O逆时针旋转60°得到的,则点![]() 与点B的距离为_______.
与点B的距离为_______.
15.已知空气的密度是0.001239![]() ,用科学记数法表示为________
,用科学记数法表示为________![]()
16.如图,在菱形![]() 中,
中,![]() ,点
,点![]() 是边
是边![]() 的中点,
的中点,![]() 是对角线
是对角线![]() 上的一个动点,若
上的一个动点,若![]() ,则
,则![]() 的最小值是_____.
的最小值是_____.
三、解下列各题(本大题共8小题,共72分)
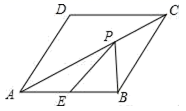
17.(8分)如图,在![]() 中,
中,![]() 于点E点,延长BC至F点使
于点E点,延长BC至F点使![]() ,连接AF,DE,DF.
,连接AF,DE,DF.
(1)求证:四边形AEFD是矩形;
(2)若![]() ,
,![]() ,
,![]() ,求AE的长.
,求AE的长.
18.(8分)分解因式:
(1)![]() ;
;
(2)![]() 。
。
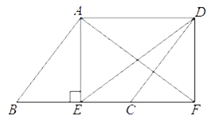
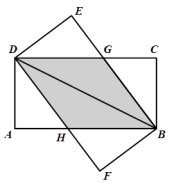
19.(8分)将两张完全相同的矩形纸片ABCD、FBED按如图方式放置,BD为重合的对角线.重叠部分为四边形DHBG,
(1)试判断四边形DHBG为何种特殊的四边形,并说明理由;
(2)若AB=8,AD=4,求四边形DHBG的面积.
20.(8分)已知x=![]() +1,y=
+1,y=![]() ﹣1,求x2+y2的值.
﹣1,求x2+y2的值.
21.(8分)如图,两个全等的Rt△AOB、Rt△OCD分别位于第二、第一象限,∠ABO=∠ODC=90°,OB、OD在x轴上,且∠AOB=30°,AB=1.
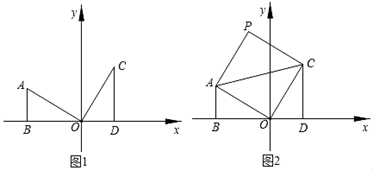
(1)如图1中Rt△OCD可以看作由Rt△AOB先绕点O顺时针旋转 度,再绕斜边中点旋转 度得到的,C点的坐标是 ;
(2)是否存在点E,使得以C、O、D、E为顶点的四边形是平行四边形,若存在,写出E点的坐标;若不存在请说明理由.
(3)如图2将△AOC沿AC翻折,O点的对应点落在P点处,求P点的坐标.
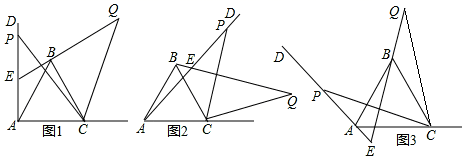
22.(10分)如图1,已知∠DAC=90°,△ABC是等边三角形,点P为射线AD上任意一点(点P与点A不重合),连结CP,将线段CP绕点C顺时针旋转60°得到线段CQ,连结QB并延长交直线AD于点E.
(1)如图1,猜想∠QEP= °;
(2)如图2,3,若当∠DAC是锐角或钝角时,其它条件不变,猜想∠QEP的度数,选取一种情况加以证明;
(3)如图3,若∠DAC=135°,∠ACP=15°,且AC=4,求BQ的长.
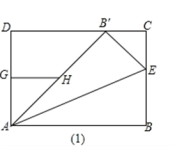
23.(10分)已知:矩形ABCD中,AB=10,AD=8,点E是BC边上一个动点,将△ABE沿AE折叠得到△AB′E。
(1)如图(1),点G和点H分别是AD和AB′的中点,若点B′在边DC上。
①求GH的长;
②求证:△AGH≌△B′CE;
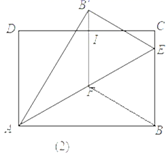
(2)如图(2),若点F是AE的中点,连接B′F,B′F∥AD,交DC于I。
①求证:四边形BEB′F是菱形;
②求B′F的长。
24.(12分)已知x=2﹣![]() ,y=2+
,y=2+![]() ,求下列代数式的值
,求下列代数式的值
(1)x2+2xy+y2;
(2)![]()
![]()
参考答案
一、选择题(每小题3分,共30分)
1、B
2、B
3、A
4、D
5、A
6、B
7、C
8、A
9、A
10、A
二、填空题(本大题共有6小题,每小题3分,共18分)
11、3
12、760
13、1
14、1
15、1.239×10-3.
16、![]()
三、解下列各题(本大题共8小题,共72分)
17、(1)见解析;(2)![]()
18、(1)![]() ;(2)
;(2)![]() .
.
19、(1)四边形DHBG是菱形,理由见解析;(2)1.
20、1
21、(1)90,180,(1,![]() );(2)存在,E的坐标为(0,
);(2)存在,E的坐标为(0,![]() )或(2,
)或(2,![]() ),或(0,﹣
),或(0,﹣![]() );(3)P(1﹣
);(3)P(1﹣![]() ,1+
,1+![]() ).
).
22、(1)∠QEP=60°;(2)∠QEP=60°,证明详见解析;(3)![]()
23、(1)①3;②详见解析;(2)①详见解析;②![]()
24、(1)11;(2)1.
广东省广州大附属中学2023-2024学年九上数学期末检测模拟试题含答案: 这是一份广东省广州大附属中学2023-2024学年九上数学期末检测模拟试题含答案,共8页。试卷主要包含了函数与,某同学用一根长为,已知下列命题等内容,欢迎下载使用。
广东省广州市广州大附属中学2023-2024学年八上数学期末达标检测模拟试题含答案: 这是一份广东省广州市广州大附属中学2023-2024学年八上数学期末达标检测模拟试题含答案,共8页。试卷主要包含了考生要认真填写考场号和座位序号等内容,欢迎下载使用。
广东省广州大附属中学2022-2023学年七年级数学第二学期期末联考试题含答案: 这是一份广东省广州大附属中学2022-2023学年七年级数学第二学期期末联考试题含答案,共6页。试卷主要包含了考生必须保证答题卡的整洁,下列命题中,正确的是,下列各式中,正确的是等内容,欢迎下载使用。












