2020年山东省枣庄市初中学业水平考试试题·数学

2020年山东省枣庄市初中学业水平考试试题·数学

注意事项：

1. 本试题分第Ⅰ卷和第Ⅱ卷两部分．第Ⅰ卷为选择题，36 分；第Ⅱ卷为非选择题，84 分；全卷共 6 页，满分 120 分．考试时间为 120 分钟．

2. 答卷时，考生务必将第Ⅰ卷和第Ⅱ卷的答案填涂或书写在答题卡指定位置上，并在本页上方空白处写上姓名和准考证号．考试结束，将试卷和答题卡一并交回.

第Ⅰ卷(选择题　共36分)

一、选择题：本大题共12小题，在每小题给出的四个选项中，只有一项是正确的，请把正确的选项选出来．每小题选对得3分，选错、不选或选出的答案超过一个均计零分．　　　　　 　　　　　　 　　　　　　

1. －的绝对值是(　　)

A. －      B. －2      C.        D. 2

2. 一副直角三角板如图放置，点 C 在 FD 的延长线上，AB∥CF，∠F＝∠ACB＝90°，则∠DBC 的度数为(　　)

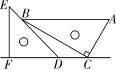
第2题图

A. 10°  B. 15°  C. 18°  D. 30°

3. 计算－－(－)的结果为(　　)

A. －  B.

C. －  D.

4. 实数 a，b 在数轴上对应点的位置如图所示，下列判断正确的是(　　)

第4题图

A. |a|＜1  B. ab＞0 

C. a＋b＞0  D. 1－a＞1

5. 不透明布袋中装有除颜色外没有其他区别的 1 个红球和 2 个白球，搅匀后从中摸出一个球，放回搅匀，再摸出一个球，两次都摸出白球的概率是(　　)

A.        B.      C.       D.

6. 如图，在△ABC 中，AB 的垂直平分线交 AB于点D，交BC于点E，连接AE.若BC＝6，AC＝5，则△ACE的周长为(　　)

A. 8      B. 11     C. 16        D. 17

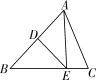
第6题图

7. 图①是一个长为2a，宽为2b(a＞b)的长方形，用剪刀沿图中虚线(对称轴)剪开，把它分成四块形状和大小完全相同的小长方形，然后按图②那样拼成一个正方形，则中间空余的部分的面积是(　　)

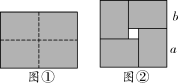
第7题图

A. ab        B. (a＋b)2    C. (a－b)2     D. a2－b2

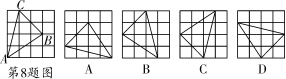
8. 下图右侧的四个三角形中，不能由△ABC经过旋转或平移得到的是(　　)

9. 对于实数a、b，定义一种新运算“”为：ab＝，这里等式右边是实数运算．例如：13＝＝－.则方程x(－2)＝－1的解是(　　)

A. x＝4      B. x＝5    C. x＝6      D. x＝7

10. 如图，平面直角坐标系中，点B在第一象限，点A在x轴的正半轴上，∠AOB＝∠B＝30°，OA＝2.将△AOB绕点O逆时针旋转90°，点B的对应点B′的坐标是(　　)

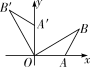
第10题图

A. (－，3)  B. (－3，)    C. (－，2＋)   D. (－1，2＋)

11. 如图，在矩形纸片ABCD中，AB＝3，点E在边BC上，将△ABE沿直线AE折叠，点B恰好落在对角线AC上的点F处，若∠EAC＝∠ECA，则AC的长是(　　)

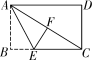
第11题图

A. 3       B. 4     C. 5     D. 6

12. 如图，已知抛物线y＝ax2＋bx＋c的对称轴为直线x＝1.给出下列结论：

①ac<0；②b2－4ac>0；③2a－b＝0；④a－b＋c＝0.其中，正确的结论有(　　)

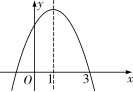
第12题图

A. 1个  B. 2个  C. 3个  D. 4个

第Ⅱ卷(非选择题　共84分)

二、填空题：本大题共6小题，满分24分．只填写最后结果，每小题填对得4分．

13. 若a＋b＝3，a2＋b2＝7，则ab＝________．

14. 已知关于x的一元二次方程(a－1)x2－2x＋a2－1＝0有一个根为x＝0，则a＝________．

15. 如图，AB是⊙O的直径，PA切⊙O于点A，线段PO交⊙O于点C.连接BC，若∠P＝36°，则∠B＝________．

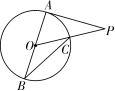
第15题图

16. 人字梯为现代家庭常用的工具(如图)．若AB，AC的长都为2 m，当α＝50°时，人字梯顶端离地面的高度AD是________m．(结果精确到0.1 m，参考数据：sin50°≈0.77，cos50°≈0.64，tan50°≈1.19)

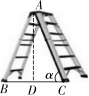
第16题图

17. 如图，E，F是正方形ABCD的对角线AC上的两点，AC＝8，AE＝CF＝2，则四边形BEDF的周长是________．

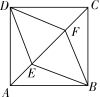
第17题图

18. 各顶点都在方格纸的格点(横竖格子线的交错点)上的多边形称为格点多边形，它的面积S可用公式S＝a＋b－1(a是多边形内的格点数，b是多边形边界上的格点数)计算，这个公式称为“皮克(Pick)定理”．如图给出了一个格点五边形，则该五边形的面积S＝________．

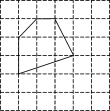
第18题图

三、解答题：本大题共7小题，满分60分．解答时，要写出必要的文字说明、证明过程或演算步骤．

19. (本题满分8分)

解不等式组并求它的所有整数解的和．

20. (本题满分8分)

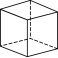
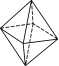
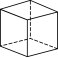
欧拉(Euler，1707年～1783年)为世界著名的数学家、自然科学家，他在数学、物理、建筑、航海等领域都做出了杰出的贡献．他对多面体做过研究，发现多面体的顶点数V(Vertex)、棱数E(Edge)、面数F(Flat surface)之间存在一定的数量关系，给出了著名的欧拉公式．

(1)观察下列多面体，并把下表补充完整：

(2)分析表中的数据，你能发现V、E、F之间有什么关系吗？请写出关系式：____________________．

21. (本题满分8分)

2020年，新型冠状病毒肆虐全球，疫情期间学生在家进行网课学习和锻炼，学习和身体健康状况都有一定的影响．为了解学生身体健康状况，某校对学生进行立定跳远水平测试．随机抽取50名学生进行测试，并把测试成绩(单位：m)绘制成不完整的频数分布表和频数分布直方图．

学生立定跳远测试成绩的频数分布表

学生立定跳远测试成绩的频数分布直方图

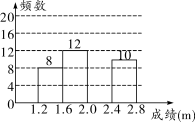
第21题图

请根据图表中所提供的信息，完成下列问题：

(1)表中a＝________，b＝________；

(2)样本成绩的中位数落在________范围内；

(3)请把频数分布直方图补充完整；

(4)该校共有1200名学生，估计该学校学生立定跳远成绩在2.4≤x＜2.8范围内的有多少人？

22. (本题满分8分)

如图，在平面直角坐标系中，一次函数y＝x＋5和y＝－2x的图象相交于点A，反比例函数y＝的图象经过点A.

(1)求反比例函数的表达式；

(2)设一次函数y＝x＋5的图象与反比例函数y＝的图象的另一个交点为B，连接OB，求△ABO的面积．

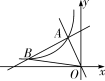
第22题图

23. (本题满分8分)

如图，在△ABC中，AB＝AC，以AB为直径的⊙O分别交AC、BC于点D、E，点F在AC的延长线上，且∠BAC＝2∠CBF.

(1)求证：BF是⊙O的切线；

(2)若⊙O的直径为4，CF＝6，求tan∠CBF.

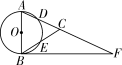
第23题图

24. (本题满分10分)

在△ABC中，∠ACB＝90°，CD是中线，AC＝BC，一个以点D为顶点的45°角绕点D旋转，使角的两边分别与AC、BC的延长线相交，交点分别为点E、F，DF与AC交于点M，DE与BC交于点N.

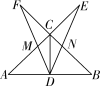
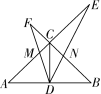
图①         　图②

第24题图

(1)如图①，若CE＝CF，求证：DE＝DF；

(2)如图②，在∠EDF绕点D旋转的过程中，试证明CD2＝CE·CF恒成立；

(3)若CD＝2，CF＝，求DN的长．

25. (本题满分10分)

如图，抛物线y＝ax2＋bx＋4交x轴于A(－3，0)，B(4，0)两点，与y轴交于点C，连接AC，BC.M为线段OB上的一个动点，过点M作PM⊥x轴，交抛物线于点P，交BC于点Q.

(1)求抛物线的表达式；

(2)过点P作PN⊥BC，垂足为点N.设M点的坐标为M(m，0)，请用含m的代数式表示线段PN的长，并求出当m为何值时PN有最大值，最大值是多少？

(3)试探究点M在运动过程中，是否存在这样的点Q，使得以A，C，Q为顶点的三角形是等腰三角形．若存在，请求出此时点Q的坐标；若不存在，请说明理由．

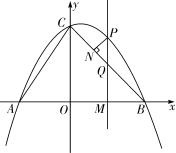
第25题图

2020年枣庄市初中学业水平考试解析

一、选择题1. D

2. B　【解析】由题意可得：∠EDF＝45°，∠ABC＝30°，∵AB∥CF，∴∠ABD＝∠EDF＝45°，∴∠DBC＝45°－30°＝15°.故选B.

3. A　【解析】－－(－)＝－＋＝－＋＝－＝－，

4. D　【解析】由数轴上a与1的位置可知：|a|>1，故选项A错误；因为a＜0，b＞0，所以ab<0，故选项B错误；因为a＜0，b＞0，所以a＋b<0，故选项C错误；因为a＜0，则1－a>1，故选项D正确；故选：D.

5. A　【解析】画树状图如解图，则共有9种等可能的结果，两次都摸到白球的有4种情况，∴两次都摸到白球的概率为.故选A.

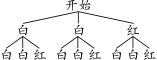
第5题解图

6. B　【解析】∵DE垂直平分AB，∴AE＝BE，∴△ACE的周长＝AC＋CE＋AE＝AC＋CE＋BE＝AC＋BC＝5＋6＝11.故选B.

7. C　【解析】由题意可得，正方形的边长为a＋b，故正方形的面积为(a＋b)2.又∵原矩形的面积为2a·2b＝4ab，∴中间空的部分的面积＝(a＋b)2－4ab＝(a－b)2.故选C.

8. B　【解析】A、可由△ABC逆时针旋转一个角度得到；B、可由△ABC翻折得到；C、可由△ABC逆时针旋转一个角度得到；D、可由△ABC逆时针旋转一个角度得到．故选B.

9. B　【解析】x⊗(－2)＝＝∴方程表达为：＝－1解得：x＝5，经检验，x＝5是原方程的解，故选：B.

10. B　【解析】如图，作B′H⊥y轴于H.由题意：OA′＝A′B′＝2，∠B′A′H＝60°，∴∠A′B′H＝30°，∴AH′＝A′B′＝1，B′H＝，∴OH＝3，∴B′(－，3)，故选B.

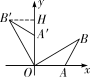
第10题解图

11. B　【解析】∵将△ABE沿直线AE折叠，点B恰好落在对角线AC上的点F处，∴AF＝AB，∠AFE＝∠B＝90°，∴EF⊥AC，∵∠EAC＝∠ECA，∴AE＝CE，∴AF＝CF，∴AC＝2AB＝6，故选B.

12. C　【解析】∵抛物线开口向下，则a＜0，∵抛物线交于y轴的正半轴，则c＞0，∴ac＜0，故①正确；∵抛物线与x轴有两个交点，∴b2－4ac>0，故②正确；∵抛物线的对称轴为直线x＝1，则－＝1，即2a＝－b，∴2a＋b＝0，故③错误；∵抛物线经过点(3，0)，且对称轴为直线x＝1，∴抛物线经过点(－1，0)，则a－b＋c＝0，故④正确；∴正确的有①②④，共3个，故选：C.

二、填空题

13. 1　【解析】(a＋b)2＝32＝9，(a＋b)2＝a2＋b2＋2ab＝9.∵a2＋b2＝7，∴2ab＝2，ab＝1.

14. －1　【解析】x＝0代入方程得：a2－1＝0解得：a＝±1∵(a－1)x2－2x＋a2－1＝0是关于x的一元二次方程∴a－1≠0，a≠1∴a＝－1

15. 27°　【解析】如图，连接AC，∵AB是⊙O的直径，∴∠ACB＝90°，∴∠B＋∠BAC＝90°，∵PA切⊙O于点A，∴∠BAP＝90°，∴∠B＝∠PAC，∵∠ACO＝∠P＋∠PAC，∠ACO＋∠BCO＝∠ACO＋∠B＝90°，∴90°－∠B＝∠B＋36°，解得∠B＝27°.

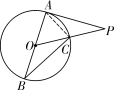
第15题解图

16. 1.5　【解析】在Rt△ADC中，∵AC＝2，∠ACD＝50°，∴sin50°＝，∴AD＝AC×sin50°＝2×0.77≈1.5

17. 8　【解析】如图，连接BD交AC于点O，∵四边形ABCD为正方形，∴BD⊥AC，OD＝OB＝OA＝OC，∵AE＝CF＝2，∴OA－AE＝OC－CF，即OE＝OF，∴四边形BEDF为平行四边形，且BD⊥EF，∴四边形BEDF为菱形，∴DE＝DF＝BE＝BF，∵AC＝BD＝8，OE＝OF＝＝2，由勾股定理得：DE＝＝＝2，∴四边形BEDF的周长＝4DE＝4×2＝8，

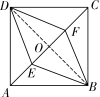
第17题解图

18. 6　【解析】由图可知：五边形内部格点有4个，故a＝4五边形边上格点有6个，故b＝6∴S＝a＋b－1＝4＋×6－1＝6.

三、解答题

19. 解：解不等式4(x＋1)≤7x＋13，得x≥－3；

解不等式x－4<，得x<2.

所以，不等式组的解集为－3≤x<2.

该不等式组的所有整数解为－3，－2，－1，0，1.

所以，该不等式组的所有整数解的和为(－3)＋(－2)＋(－1)＋0＋1＝－5.

20. 解：(1)填表如下：

(2)据上表中的数据规律发现，多面体的顶点数V、棱数E、面数F之间存在关系式：V＋F－E＝2.

21. 解：(1)由统计图可得a＝8，b＝50－8－12－10＝20；

(2)∵有50名学生进行测试，第25和26名的成绩和的平均数为中位数

∴样本成绩的中位数落在2.0≤x<2.4范围内；

(3)由(1)知，b＝20，补全的频数分布直方图如右图所示；

学生立定跳远测试成绩的频数分布直方图

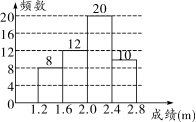
第21题解图

(4)1200×＝240(人)，

答：估计该学校学生立定跳远成绩在2.4≤x<2.8范围内有240人．

22. 解：(1)由题意：联立直线方程，可得，故A点坐标为(－2，4)

将A(－2，4)代入反比例函数表达式y＝，有4＝，∴k＝－8

故反比例函数的表达式为y＝－

(2)联立直线y＝x＋5与反比例函数y＝－，

解得x1＝－2，x2＝－8，当x＝－8时，y＝1，故B(－8，1)

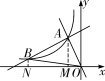
第22题解图

如图，过A，B两点分别作x轴的垂线，交x轴于M、N两点，由模型可知

S梯形AMNB＝S△AOB，

∴S梯形AMNB＝S△AOB＝(y1＋y2)(x1－x2)×＝(1＋4)×[(－2)－(－8)]×＝5×6×＝15

23. (1)证明：如解图①，连接AE.

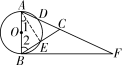
第23题解图①

∵AB是⊙O的直径，

∴∠AEB＝90°，∠1＋∠2＝90°.

∵AB＝AC，

∴2∠1＝∠BAC.

∵∠BAC＝2∠CBF，

∴∠1＝∠CBF.

∴∠CBF＋∠2＝90°，即∠ABF＝90°.

∵AB是⊙O的直径，

∴直线BF是⊙O的切线.

(2)解：如解图②，过点C作CH⊥BF于点H.

∵AB＝AC，⊙O的直径为4，

∴AC＝4.

∵CF＝6，∠ABF＝90°，

∴BF＝＝＝2.

∵∠CHF＝∠ABF，∠F＝∠F，

∴△CHF∽△ABF.

∴＝，即＝.

∴CH＝，HF＝＝＝.

∴BH＝BF－HF＝2－＝.

∴tan∠CBF＝＝＝.

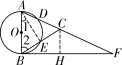
第23题解图②

24. (1)证明：∵∠ACB＝90°，AC＝BC，CD是中线，

∴∠BCD＝∠ACD＝45°，∠BCE＝∠ACF＝90°，

∴∠DCE＝∠DCF＝135°.

在△DCE与△DCF中，，

∴△DCE≌△DCF.

∴DE＝DF；

(2)证明：∵∠DCF＝∠DCE＝135°，

∴∠CDF＋∠F＝180°－135°＝45°

∵∠CDF＋∠CDE＝45°，

∴∠F＝∠CDE.

∴△CDF∽△CED.

∴＝，即CD2＝CE·CF.

(3)如解图，过D作DG⊥BC于点G，

则∠DGN＝∠ECN＝90°，CG＝DG.

当CD＝2，CF＝时，

由CD2＝CE·CF，得CE＝2.

在Rt△DCG中，

CG＝DG＝CD·sin∠DCG＝2×sin45°＝.

∵∠ECN＝∠DGN，∠ENC＝∠DNG，

∴△CEN∽△GDN.

∴＝＝＝2，

∴GN＝CG＝×＝.

∴DN＝＝＝.

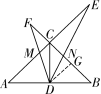
第24题解图

25. 解：(1)将A(－3，0)，B(4，0)代入y＝ax2＋bx＋4，得，解之，得.

所以，抛物线的表达式为y＝－x2＋x＋4.

(2)由y＝－x2＋x＋4，得C(0，4)．

将点B(4，0)、C(0，4)代入y＝kx＋b，得，解之，得.

所以，直线BC的表达式为：y＝－x＋4.

由M(m，0)，得P(m，－m2＋m＋4)，Q(m，－m＋4)．

∴PQ＝－m2＋m＋4＋m－4＝－m2＋m

∵OB＝OC，∴∠ABC＝∠OCB＝45°.

∴∠PQN＝∠BQM＝45°.

∴PN＝PQsin45°＝(－m2＋m)＝－m2＋m.

＝－(m－2)2＋.

∵－<0

∴当m＝2时，PN有最大值，最大值为.

(3)存在，理由如下：由点A(－3，0)，C(0，4)，知AC＝5.

①当AC＝CQ时，如解图，过Q作QE⊥y轴于点E，易得CQ2＝EQ2＋CE2＝m2＋[4－(－m＋4)]2＝2m2，

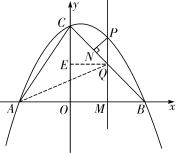
第25题解图

由2m2＝25，得m1＝，m2＝－(舍)

此时，点Q(，)；

②当AC＝AQ时，则AQ＝AC＝5.

在Rt△AMQ中，由勾股定理，得[m－(－3)]2＋(－m＋4)2＝25.

解之，得m＝1或m＝0(舍)

此时，点Q(1，3)；

③当CQ＝AQ时，

由2m2＝[m－(－3)]2＋(－m＋4)2，得m＝(舍)．

综上知所述，可知满足条件的点Q有两个，坐标分别为：Q(1，3)，Q(，)．