





专题24 定点定长构造辅助圆 2022-2023学年九年级数学上册常考点微专题提分精练(人教版)(解析+原卷)
展开![]()
专题24 定点定长构造辅助圆
1.如图,已知![]() ,
,![]() ,
,![]() ,则
,则![]() 的度数为
的度数为![]()
![]()
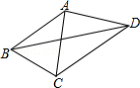
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.如图,在四边形![]() 中,
中,![]() ,
,![]() 则
则![]() 的大小是
的大小是![]()
![]()
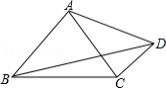
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.如图,在矩形![]() 中,已知
中,已知![]() ,
,![]() ,点
,点![]() 是
是![]() 边上一动点(点
边上一动点(点![]() 不与
不与![]() ,
,![]() 重合),连接
重合),连接![]() ,作点
,作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,则线段
,则线段![]() 的最小值为
的最小值为![]()
![]()
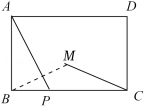
A.2 B.![]() C.3 D.
C.3 D.![]()
4.如图,正方形![]() 中,
中,![]() 为
为![]() 中点,
中点,![]() ,
,![]() ,
,![]() 交
交![]() 于
于![]() ,则
,则![]() 的度数为
的度数为![]()
![]()
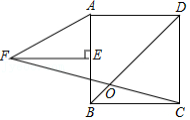
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.如图,已知等边![]() 的边长为8,以
的边长为8,以![]() 为直径的圆交
为直径的圆交![]() 于点
于点![]() .以
.以![]() 为圆心,
为圆心,![]() 长为半径作图,
长为半径作图,![]() 是
是![]() 上一动点,
上一动点,![]() 为
为![]() 的中点,当
的中点,当![]() 最大时,
最大时,![]() 的长为
的长为![]()
![]()
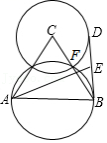
A.![]() B.
B.![]() C.
C.![]() D.12
D.12
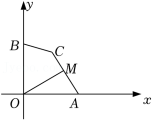
6.如图,点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,
,![]() 为坐标平面内一点,
为坐标平面内一点,![]() ,点
,点![]() 为线段
为线段![]() 的中点,连接
的中点,连接![]() ,
,![]() 的最大值为 .
的最大值为 .
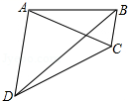
7.如图,四边形![]() 中,
中,![]() ,且
,且![]() ,若
,若![]() ,则
,则![]() ,
,![]() .
.
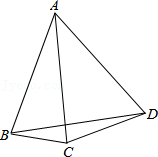
8.如图所示,![]() ,
,![]() ,则
,则![]() .
.
9.如图,四边形![]() 中,
中,![]() 、
、![]() 分别是
分别是![]() ,
,![]() 的中垂线,
的中垂线,![]() ,
,![]() ,则
,则![]() ,
,![]() .
.
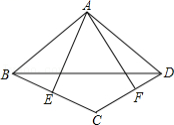
10.如图,![]() ,如果
,如果![]() 是
是![]() 的
的![]() 倍,那么
倍,那么![]() 是
是![]() 的 倍.
的 倍.
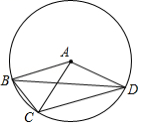
11.如图,矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 是直线
是直线![]() 上的一个动点,
上的一个动点,![]() ,
,![]() 沿
沿![]() 翻折形成
翻折形成![]() ,连接
,连接![]() 、
、![]() ,则
,则![]() 的最小值是 ,点
的最小值是 ,点![]() 到线段
到线段![]() 的最短距离是 .
的最短距离是 .
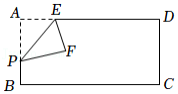
12.如图,在![]() 中,
中,![]() ,过点
,过点![]() 作
作![]() ,
,![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.![]() 是
是![]() 的中点,连接
的中点,连接![]() 交
交![]() 于
于![]() .
.
(1)若![]() ,求
,求![]() 的度数;
的度数;
(2)若![]() ,且
,且![]() ,求四边形
,求四边形![]() 的面积.
的面积.
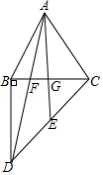
13.如图,![]() ,
,![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
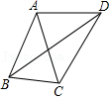
14.圆的定义:在同一平面内,到定点的距离等于定长的所有点所组成的图形.
(1)已知:如图1,![]() ,请利用圆规画出过
,请利用圆规画出过![]() 、
、![]() .
.![]() 三点的圆.若
三点的圆.若![]() ,则
,则![]() .
.
如图,![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
(2)已知,如图2.点![]() 为
为![]() 边的中点,将
边的中点,将![]() 沿
沿![]() 方向平移2个单位长度,点
方向平移2个单位长度,点![]() 、
、![]() 、
、![]() 的对应点分别为点
的对应点分别为点![]() 、
、![]() 、
、![]() ,求四边形
,求四边形![]() 的面积和
的面积和![]() 的大小.
的大小.
(3)如图3,将![]() 边沿
边沿![]() 方向平移
方向平移![]() 个单位至
个单位至![]() ,是否存在这样的
,是否存在这样的![]() ,使得直线
,使得直线![]() 上有一点
上有一点![]() ,满足
,满足![]() 且此时四边形
且此时四边形![]() 的面积最大?若存在,求出四边形
的面积最大?若存在,求出四边形![]() 面积的最大值及平移距离
面积的最大值及平移距离![]() ,若不存在,说明理由.
,若不存在,说明理由.
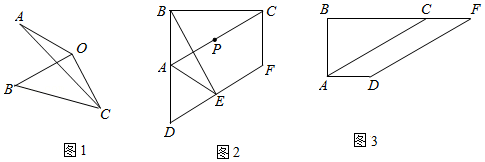
15.在![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 分别平分
分别平分![]() 和
和![]() ,求证:
,求证:![]() .
.
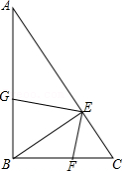
16.如图,在![]() 中,
中,![]() ,
,![]() 垂直平分
垂直平分![]() ,且
,且![]() ,连接
,连接![]()
(1)求证:![]() ;
;
(2)设![]() 交
交![]() 于点
于点![]() ,若
,若![]() 是等腰三角形,求
是等腰三角形,求![]() 的度数.
的度数.
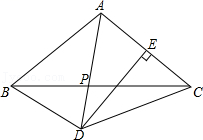
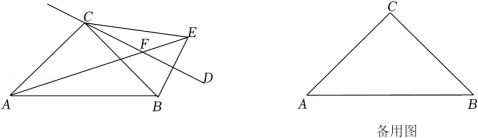
17.【阅读】
辅助线是几何解题中沟通条件与结论的桥梁.在众多类型的辅助线中,辅助圆作为一条曲线型辅助线,显得独特而隐蔽.
性质:如图①,若![]() ,则点
,则点![]() 在经过
在经过![]() ,
,![]() ,
,![]() 三点的圆上.
三点的圆上.
【问题解决】
运用上述材料中的信息解决以下问题:
(1)如图②,已知![]() .
.
求证:![]() .
.
(2)如图③,点![]() ,
,![]() 位于直线
位于直线![]() 两侧.用尺规在直线
两侧.用尺规在直线![]() 上作出点
上作出点![]() ,使得
,使得![]() .(要求:要有画图痕迹,不用写画法)
.(要求:要有画图痕迹,不用写画法)
(3)如图④,在四边形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在
在![]() 的延长线上,连接
的延长线上,连接![]() ,
,![]() .
.
求证:![]() 是
是![]() 外接圆的切线.
外接圆的切线.
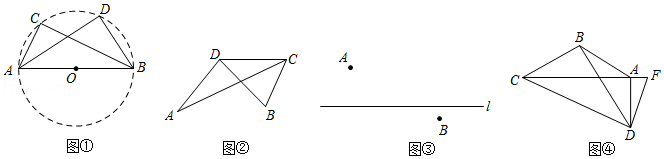
18.在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 的中点,若等腰
的中点,若等腰![]() 绕点
绕点![]() 逆时针旋转,得到等腰
逆时针旋转,得到等腰![]() △
△![]() ,设旋转角为
,设旋转角为![]() ,记直线
,记直线![]() 与
与![]() 的交点为
的交点为![]() .
.
(1)如图1,当![]() 时,线段
时,线段![]() 的长等于 ,线段
的长等于 ,线段![]() 的长等于 ;(直接填写结果)
的长等于 ;(直接填写结果)
(2)如图2,当![]() 时,求证:
时,求证:![]() ,且
,且![]() ;
;
(3)求点![]() 到
到![]() 所在直线的距离的最大值.(直接写出结果)
所在直线的距离的最大值.(直接写出结果)
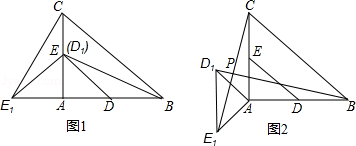
19.如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上,并且
上,并且![]() ,点
,点![]() 为
为![]() 边上的动点,将
边上的动点,将![]() 沿直线
沿直线![]() 翻折,点
翻折,点![]() 落在点
落在点![]() 处,求点
处,求点![]() 到边
到边![]() 距离的最小值.
距离的最小值.
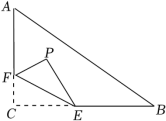
20.如图,![]() 中,
中,![]() ,
,![]() ,过点
,过点![]() 任作一条直线
任作一条直线![]() ,将线段
,将线段![]() 沿直线
沿直线![]() 翻折得线段
翻折得线段![]() ,直线
,直线![]() 交直线
交直线![]() 于点
于点![]() .
.
(1)小智同学通过思考推得当点![]() 在
在![]() 上方时,
上方时,![]() 的角度是不变的,请按小智的思路帮助小智完成以下推理过程:
的角度是不变的,请按小智的思路帮助小智完成以下推理过程:
![]() ,
,
![]() 、
、![]() 、
、![]() 三点在以
三点在以![]() 为圆心以
为圆心以![]() 为半径的圆上.
为半径的圆上.
![]()
![]()
![]() .
.
(2)若![]() ,求
,求![]() 的长.
的长.
(3)线段![]() 最大值为 ;若取
最大值为 ;若取![]() 的中点
的中点![]() ,则线段
,则线段![]() 的最小值为 .
的最小值为 .
专题25 定弦定角构造辅助圆-【微专题】2022-2023学年九年级数学上册常考点微专题提分精练(人教版): 这是一份专题25 定弦定角构造辅助圆-【微专题】2022-2023学年九年级数学上册常考点微专题提分精练(人教版),文件包含专题25定弦定角构造辅助圆原卷版docx、专题25定弦定角构造辅助圆解析版docx等2份试卷配套教学资源,其中试卷共29页, 欢迎下载使用。
专题24 定点定长构造辅助圆-【微专题】2022-2023学年九年级数学上册常考点微专题提分精练(人教版): 这是一份专题24 定点定长构造辅助圆-【微专题】2022-2023学年九年级数学上册常考点微专题提分精练(人教版),文件包含专题24定点定长构造辅助圆原卷版docx、专题24定点定长构造辅助圆解析版docx等2份试卷配套教学资源,其中试卷共29页, 欢迎下载使用。
专题28 圆中将军饮马-【微专题】2022-2023学年九年级数学上册常考点微专题提分精练(人教版): 这是一份专题28 圆中将军饮马-【微专题】2022-2023学年九年级数学上册常考点微专题提分精练(人教版),文件包含专题28圆中将军饮马原卷版docx、专题28圆中将军饮马解析版docx等2份试卷配套教学资源,其中试卷共29页, 欢迎下载使用。












