2022-2023学年贵州遵义市达兴中学数学七年级第二学期期末学业水平测试模拟试题含答案

2022-2023学年贵州遵义市达兴中学数学七年级第二学期期末学业水平测试模拟试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项

1．考试结束后，请将本试卷和答题卡一并交回．

2．答题前，请务必将自己的姓名、准考证号用0．5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置．

3．请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符．

4．作答选择题，必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑；如需改动，请用橡皮擦干净后，再选涂其他答案．作答非选择题，必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答，在其他位置作答一律无效．

5．如需作图，须用2B铅笔绘、写清楚，线条、符号等须加黑、加粗．

一、选择题(每小题3分,共30分)

1．下列表格是二次函数的自变量x与函数值y的对应值，判断方程（为常数）的一个解x的范围是

A． B．

C． D．

2．对于函数 y＝3-x，下列结论正确的是（    ）

A．y 的值随 x 的增大而增大 B．它的图象必经过点（-1,3）

C．它的图象不经过第三象限 D．当 x＞1 时，y＜0.

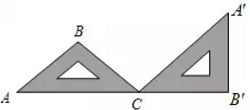
3．如图，一块等腰直角的三角板，在水平桌面上绕点按顺时针方向旋转到的位置，使三点共线，那么旋转角度的大小为(　　)

A． B． C． D．

4．若，则的值用、可以表示为                     （　 　）

A． B． C． D．

5．已知P1（﹣3，y1），P2（2，y2）是一次函数y=﹣x﹣1的图象上的两个点，则y1，y2的大小关系是（　　）

A．y1=y2 B．y1＜y2 C．y1＞y2 D．不能确定

6．某校将举办一场“中国汉字听写大赛”，要求每班推选一名同学参加比赛，为此，八年级（1)班组织了五轮班级选拔赛，下表记录了该班甲、乙、丙、丁四名同学五轮选拔赛成绩的平均数与方差S2：根据表中数据，要从中选择一名成绩好又发挥稳定的同学参赛，应该选择（　　）　

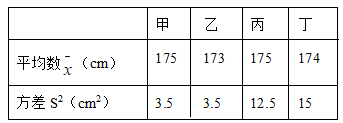
A．甲 B．乙 C．丙 D．丁

7．已知a是方程的一个根，则代数式的值是（　　）

A．6 B．5 C． D．

8．如图，AB∥CD，BP和CP分别平分∠ABC和∠DCB，AD过点P，且与AB垂直．若AD＝8，则点P到BC的距离是（　　）

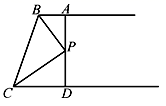
A．8 B．6 C．4 D．2

9．为了增强学生体质，学校发起评选“健步达人”活动，小明用计步器记录自己一个月（30天）每天走的步数，并绘制成如下统计表：

在每天所走的步数这组数据中，众数和中位数分别是（　　）

A．1.3，1.1 B．1.3，1.3 C．1.4，1.4 D．1.3，1.4

10．下列各式中从左到右的变形，是因式分解的是（　　）

A．a2b+ab2＝ab（a+b） B．x2+x﹣5＝（x﹣2）（x+3）+1

C．x2+1＝x（x+） D．（a+3）（a﹣3）＝a2﹣9

二、填空题(本大题共有6小题，每小题3分，共18分)

11．距离地面2m高的某处把一物体以初速度v0(m/s)竖直向上抛物出，在不计空气阻力的情况下，其上升高度s(m)与抛出时间t(s)满足： (其中g是常数，通常取10m/s2).若v0=10m/s，则该物体在运动过程中最高点距地面_________m.

12．已知反比例函数的图象经过第一、三象限，则常数的取值范围是_____．

13．如果三角形三边长分别为，k，，则化简得___________．

14．阅读下面材料：

在数学课上，老师提出如下问题：

已知：如图，及边的中点．

求作：平行四边形．

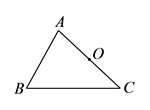
①连接并延长，在延长线上截取；

②连接、．

所以四边形就是所求作的平行四边形．

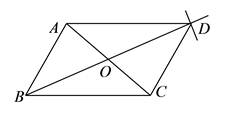
老师说：“小敏的作法正确．

请回答：小敏的作法正确的理由是__________．

15．某地区为了增强市民的法治观念，随机抽取了一部分市民进行一次知识竞赛，将竞赛成绩（得分取整数）整理后分成五组并绘制成如图所示的频数直方图.请结合图中信息，解答下列问题：

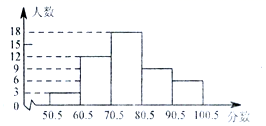
抽取了多少人参加竞赛？

这一分数段的频数、频率分别是多少？

这次竞赛成绩的中位数落在哪个分数段内？

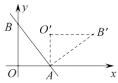
16．如图，直线与轴、轴分别交于两点，把绕点顺时针旋转后得到，则点的坐标为____．

三、解下列各题(本大题共8小题，共72分)

17．（8分）为了让学生拓展视野、丰富知识，加深与自然和文化的亲近感,增加对集体生活方式和社会公共道德的体验,我区某中学决定组织部分师生去随州炎帝故里开展研学旅行活动.在参加此次活动的师生中,若每位老师带个学生,还剩个学生没人带;若每位老师带个学生，就有一位老师少带个学生.为了安全,既要保证所有师生都有车坐,又要保证每辆客车上至少要有名老师.现有甲、乙两种大客车，它们的载客量和租金如表所示.

（1）参加此次研学旅行活动的老师有       人；学生有      人；租用客车总数为      辆；

（2）设租用辆乙种客车，租车费用为元，请写出与之间的函数关系式；

（3）在（2）的条件下，学校计划此次研学旅行活动的租车总费用不超过元，你能得出哪几种不同的租车方案？其中哪种租车方案最省钱？请说明理由.

18．（8分）某公司需招聘一名员工，对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核．甲、乙、丙各项得分如下表：

（1）根据三项得分的平均分，从高到低确定三名应聘者的排名顺序．

（2）该公司规定：笔试，面试、体能得分分别不得低于80分，80分，70分，并按60%，30%，10%的比例计入总分（不计其他因素条件），请你说明谁将被录用．

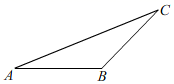
19．（8分）如图，已知中，，请用尺规作出AB边的高线请留作图痕迹，不写作法

20．（8分）（1）已知，，求的值.

（2）若，求的平方根.

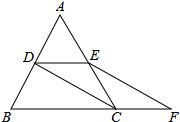
21．（8分）如图，等边的边长是4，，分别为，的中点，延长至点，使，连接和．

(1)求证：；

(2)求的长；

(3)求四边形的面积．

22．（10分）某G20商品专卖店每天的固定成本为400元，其销售的G20纪念徽章每个进价为3元，销售单价与日平均销售的关系如下表：

 (1)设销售单价比每个进价多x元，用含x的代数式表示日销售量．

(2)若要使日均毛利润达到1840元(毛利润＝总售价﹣总进价﹣固定成本)，且尽可能多的提升日销售量，则销售单价应定为多少元？

23．（10分）已知关于的一元二次方程: ;

(1)求证:无论为何值，方程总有实数根;

(2)若方程的一个根是2，求另一个根及的值.

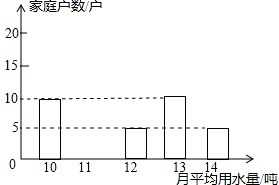
24．（12分）为了倡导“节约用水，从我做起”，南沙区政府决定对区直属机关300户家庭的用水情况作一次调查，区政府调查小组随机抽查了其中50户家庭一年的月平均用水量（单位：吨），调查中发现每户用水量均在10﹣14吨/月范围，并将调查结果制成了如图所示的条形统计图．

（1）请将条形统计图补充完整；

（2）这50户家庭月用水量的平均数是　   　，众数是　   　，中位数是　   　；

（3）根据样本数据，估计南沙区直属机关300户家庭中月平均用水量不超过12吨的约有多少户？

参考答案

一、选择题(每小题3分,共30分)

1、C

2、C

3、D

4、C

5、C

6、A

7、B

8、C

9、B

10、A

二、填空题(本大题共有6小题，每小题3分，共18分)

11、7

12、k＞

13、11-3k.

14、对角线互相平分的四边形是平行四边形

15、（1）抽取了人参加比赛；（2）频数为，频数为0.25；（3）

16、（7，3）

三、解下列各题(本大题共8小题，共72分)

17、（1）；；；（2）；（3）共有种租车方案：方案一：租用甲种客车辆，乙种客车辆；方案二：租用甲种客车辆，乙种客车辆；方案三：租用甲种客车辆，乙种客车辆；最节省费用的租车方案是：租用甲种客车辆，乙种客车辆；

18、（1）丙，乙，甲；（2）甲被录用．

19、作图见解析.

20、（1）；（2）

21、 (1)证明见解析；(2)EF=；(3).

22、 (1)﹣40x+600；(2)销售单价应定为10元．

23、（1）详见解析；（2），

24、 (1)补图见解析；（2）11.6，11，11；（）210户.