


2022-2023学年福建省罗源第二中学七下数学期末学业水平测试模拟试题含答案
展开2022-2023学年福建省罗源第二中学七下数学期末学业水平测试模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项
1.考试结束后,请将本试卷和答题卡一并交回.
2.答题前,请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置.
3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符.
4.作答选择题,必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选涂其他答案.作答非选择题,必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效.
5.如需作图,须用2B铅笔绘、写清楚,线条、符号等须加黑、加粗.
一、选择题(每小题3分,共30分)
1.在Rt△ABC中,斜边长AB=3,AB²+AC²+BC²的值为( )
A.18 B.24 C.15 D.无法计算
2.下列命题中是假命题的是( )
A.一组对边平行且相等的四边形是平行四边形
B.一组对边相等且有一个角是直角的四边形是矩形
C.一组邻边相等的平行四边形是菱形
D.一组邻边相等的矩形是正方形
3.关于直线l:y=kx+k(k≠0),下列说法不正确的是( )
A.点(0,k)在l上
B.l经过定点(-1,0)
C.当k>0时,y随x的增大而增大
D.l经过第一、二、三象限
4.某市为解决部分市民冬季集中取暖问题,需铺设一条长4000米的管道,为尽量减少施工对交通造成的影响,施工时“…”,设实际每天铺设管道x米,则可得方程![]() =20,根据此情景,题中用“…”表示的缺失的条件应补为( )
=20,根据此情景,题中用“…”表示的缺失的条件应补为( )
A.每天比原计划多铺设10米,结果延期20天完成
B.每天比原计划少铺设10米,结果延期20天完成
C.每天比原计划多铺设10米,结果提前20天完成
D.每天比原计划少铺设10米,结果提前20天完成
5.若线段2a+1,a,a+3能构成一个三角形,则a的范围是( )
A.a>0 B.a>1 C.a>2 D.1<a<3
6.函数![]() 中,自变量x的取值范围是( )
中,自变量x的取值范围是( )
A.x>1 B.x<1 C.![]() D.
D.![]()
7.甲、乙、丙三个旅游团的游客人数都相等,且每个团游客的平均年龄都是35岁,这三个团游客年龄的方差分别是![]() ,
,![]() ,
,![]() ,导游小方最喜欢带游客年龄相近的团队,若在这三个团中选择一个,则他应选( )
,导游小方最喜欢带游客年龄相近的团队,若在这三个团中选择一个,则他应选( )
A.甲队 B.乙队 C.丙队 D.哪一个都可以
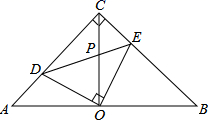
8.如图,在等腰直角△ABC中,∠ACB=90°,O是斜边AB的中点,点D,E分别在直角边AC,BC上,且∠DOE=90°,DE交OC于点P,则下列结论:(1)AD+BE=AC;(2)AD2+BE2=DE2;(3)△ABC的面积等于四边形CDOE面积的2倍;(4)OD=OE,其中正确的结论有( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
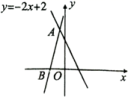
9.如图,经过点![]() 的直线
的直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,则不等式
,则不等式![]() 的解集为( )
的解集为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.下列函数中,表示y是x的正比例函数的是( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(本大题共有6小题,每小题3分,共18分)
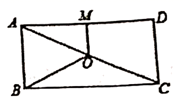
11.如图,点O是矩形ABCD的对角线AC的中点,M是AD的中点,若OM=3,BC=8,则OB的长为 ________。
12.观察下列各式:![]() ,
,![]() ,
,![]() ,……请你将发现的规律用含自然数n(n≥1)的等式表示出来__________________.
,……请你将发现的规律用含自然数n(n≥1)的等式表示出来__________________.
13.如图,菱形![]() 中,
中,![]() ,点
,点![]() 是直线
是直线![]() 上的一点.已知
上的一点.已知![]() 的面积为6,则线段
的面积为6,则线段![]() 的长是_____.
的长是_____.
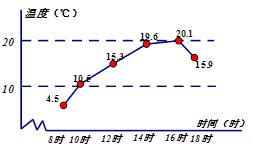
14.已知杭州市某天六个整点时的气温绘制成的统计图,则这六个整点时气温的中位数是 .
15.用反证法证明命题“在直角三角形中,至少有一个锐角不大于 45°”时第一步先假设所求证的结论不成立,即问题表述为______.
16.当x=1时,分式![]() 的值是_____.
的值是_____.
三、解下列各题(本大题共8小题,共72分)
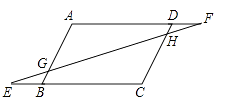
17.(8分)如图,在□ABCD中,点E、F分别在边CB、AD的延长线上,且BE=DF,EF分别与AB、CD交于点G、H,求证:AG=CH.
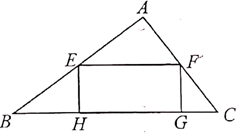
18.(8分)如图,要从一块![]() 的白铁皮零料上截出一块矩形
的白铁皮零料上截出一块矩形![]() 白铁皮.已知
白铁皮.已知![]() ,
,![]() ,要求截出的矩形的长与宽的比为
,要求截出的矩形的长与宽的比为![]() ,且较长边在
,且较长边在![]() 上,点
上,点![]() 分别在
分别在![]() 上,所截矩形的长和宽各是多少?
上,所截矩形的长和宽各是多少?
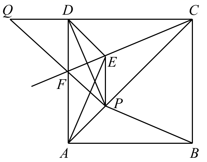
19.(8分)如图,在边长为![]() 的正方形ABCD中,作∠ACD的平分线交AD于F,过F作直线AC的垂线交AC于P,交CD的延长线于Q,又过P作AD的平行线与直线CF交于点E,连接DE,AE,PD,PB.
的正方形ABCD中,作∠ACD的平分线交AD于F,过F作直线AC的垂线交AC于P,交CD的延长线于Q,又过P作AD的平行线与直线CF交于点E,连接DE,AE,PD,PB.
(1)求AC,DQ的长;
(2)四边形DFPE是菱形吗?为什么?
(3)探究线段DQ,DP,EF之间的数量关系,并证明探究结论;
(4)探究线段PB与AE之间的数量关系与位置关系,并证明探究结论.
20.(8分)一个二次函数的图象经过(﹣1,﹣1),(0,0),(1,9)三点
(1)求这个二次函数的解析式.
(2)若另外三点(x1,21),(x2,21),(x1+x2,n)也在该二次函数图象上,求n的值.
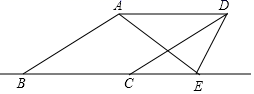
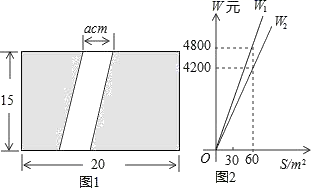
21.(8分)如图,△ABC是等边三角形,BD是中线,P是直线BC上一点.
(1) 若CP=CD,求证:△DBP是等腰三角形;
(2) 在图①中建立以△ABC的边BC的中点为原点,BC所在直线为x轴,BC边上的高所在直线为y轴的平面直角坐标系,如图②,已知等边△ABC的边长为2,AO=![]() ,在x轴上是否存在除点P以外的点Q,使△BDQ是等腰三角形?如果存在,请求出Q点的坐标;如果不存在,请说明由.
,在x轴上是否存在除点P以外的点Q,使△BDQ是等腰三角形?如果存在,请求出Q点的坐标;如果不存在,请说明由.
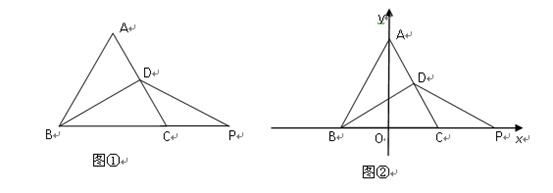
22.(10分)如图1,为美化校园环境,某校计划在一块长为20m,宽为15m的长方形空地上修建一条宽为a(m)的甬道,余下的部分铺设草坪建成绿地.
(1)甬道的面积为 m2,绿地的面积为 m2(用含a的代数式表示);
(2)已知某公园公司修建甬道,绿地的造价W1(元),W2(元)与修建面积S之间的函数关系如图2所示.①园林公司修建一平方米的甬道,绿地的造价分别为 元, 元.②直接写出修建甬道的造价W1(元),修建绿地的造价W2(元)与a(m)的关系式;③如果学校决定由该公司承建此项目,并要求修建的甬道宽度不少于2m且不超过5m,那么甬道宽为多少时,修建的甬道和绿地的总造价最低,最低总造价为多少元?
23.(10分)解方程:x2﹣6x+8=1.
24.(12分)解方程:(1-3y)2+2(3y-1)=1.
参考答案
一、选择题(每小题3分,共30分)
1、A
2、B
3、D
4、C
5、B
6、C
7、A
8、D
9、C
10、B
二、填空题(本大题共有6小题,每小题3分,共18分)
11、5
12、![]()
13、![]()
14、15.6
15、假设在直角三角形中,两个锐角都大于45°.
16、![]()
三、解下列各题(本大题共8小题,共72分)
17、证明见解析.
18、所截矩形的长是![]() ,宽是
,宽是![]()
19、(1)AC=![]() ,QD=
,QD=![]() ;(2)是菱形,理由见解析;(3)DP2+ EF2=4QD2,理由见解析;(4)垂直且相等,理由见解析.
;(2)是菱形,理由见解析;(3)DP2+ EF2=4QD2,理由见解析;(4)垂直且相等,理由见解析.
20、 (1)y=4x2+5x;(2)n=1.
21、(1)见解析(2)P1(-![]() -1,0),P2(0,0)P3(
-1,0),P2(0,0)P3(![]() +1,0)
+1,0)
22、(1)15a、(300﹣15a);(2)①①80、70;;②W1=80×15a=1200a,W2=70(300﹣15a)=﹣1050a+21000;③甬道宽为2米时,修建的甬道和绿地的总造价最低,最低总造价为21300元;
23、x1=2 x2=2.
24、![]()
福建省龙岩五中学2022-2023学年数学七下期末学业水平测试模拟试题含答案: 这是一份福建省龙岩五中学2022-2023学年数学七下期末学业水平测试模拟试题含答案,共8页。试卷主要包含了答题时请按要求用笔,计算×的结果是,正十边形的每一个内角的度数为等内容,欢迎下载使用。
2022-2023学年陈经纶中学七下数学期末学业水平测试模拟试题含答案: 这是一份2022-2023学年陈经纶中学七下数学期末学业水平测试模拟试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁等内容,欢迎下载使用。
2022-2023学年福建省邵武市四中学片区数学七下期末学业水平测试模拟试题含答案: 这是一份2022-2023学年福建省邵武市四中学片区数学七下期末学业水平测试模拟试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,若分式的值为0,则x的值为,化简的结果是,已知y=等内容,欢迎下载使用。












