山东省重点中学2022-2023学年七下数学期末学业质量监测试题含答案

这是一份山东省重点中学2022-2023学年七下数学期末学业质量监测试题含答案，共7页。试卷主要包含了下列定理中，没有逆定理的是，若分式有意义，则x的取值范围是等内容，欢迎下载使用。
山东省重点中学2022-2023学年七下数学期末学业质量监测试题（时间：120分钟             分数：120分） 学校_______            年级_______        姓名_______ 注意事项：1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。回答非选择题时，将答案写在答题卡上，写在本试卷上无效。3．考试结束后，将本试卷和答题卡一并交回。 一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．.函数的自变量x的取值范围是（    ）A． B．且 C． D．且2．下列等式一定成立的是（　　）A． B． C． D．3．我校开展了主题为“青春·梦想”的艺术作品征集活动、从八年级某六个班中收集到的作品数量（单位：件）统计如图，则这组数据的众数、中位数、平均数依次是（    ）A．48，48，48 B．48，47.5，47.5C．48，48，48.5 D．48，47.5，48.54．为了调查某校同学的体质健康状况，随机抽查了若干名同学的每天锻炼时间如表：每天锻炼时间（分钟）20406090学生数2341则关于这些同学的每天锻炼时间，下列说法错误的是（　　）A．众数是60 B．平均数是21 C．抽查了10个同学 D．中位数是505．已知关于x的一次函数y＝kx＋2k－3的图象经过原点，则k的值为（     ）A． B． C． D．6．下列定理中，没有逆定理的是（　　）A．两直线平行，同位角相等B．全等三角形的对应边相等C．全等三角形的对应角相等D．在角的内部，到角的两边距离相等的点在角的平分线上7．如图，在矩形ABCD中对角线AC、BD相交于点O，∠ACB=60°，则∠AOB的大小为（     ）A．30° B．60° C．120° D．150°8．若分式有意义，则x的取值范围是（　　）A．x≠1 B．x≠﹣1 C．x＝1 D．x＝﹣19．下列几组数中，不能作为直角三角形三边长度的是（　　）A．3，4，5 B．5，7，8 C．8，15，17 D．1，10．如图，CE，BF分别是△ABC的高线，连接EF，EF=6，BC=10，D、G分别是EF、BC的中点，则DG的长为    （    ）A．6 B．5 C．4 D．311．如图，在已知的△ABC中，按以下步骤作图：①分别以A，B为圆心，以大于AB的长为半径作弧，两弧相交于两点EF；②作直线EF交BC于点D连接AD．若AD＝AC，∠C＝40°，则∠BAC的度数是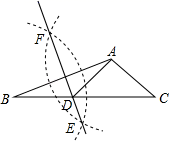（    ）A．105° B．110° C．I15° D．120°12．如图，中，平分，交于，交于，若，则四边形的周长是（ ）A． B． C． D．二、填空题（每题4分，满分20分，将答案填在答题纸上）13．已知不等式组的解集如图所示（原点没标出，数轴长度为1，黑点和圆圈均在整数的位置），则a的值为______.14．如图，Rt△ABC中，∠C=90°，AC=2，BC=5，点D是BC边上一点且CD=1，点P是线段DB上一动点，连接AP，以AP为斜边在AP的下方作等腰Rt△AOP．当P从点D出发运动至点B停止时，点O的运动路径长为_____．15．若关于x的方程无解，则m=　   　．16．直线沿轴平行的方向向下平移个单位，所得直线的函数解析式是_________17．计算：____．三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）18．（5分）如图，在平面直角坐标系中，四边形ABCD是矩形，AD∥x轴，A（，），AB=1，AD=1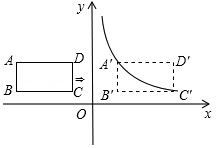．（1）直接写出B、C、D三点的坐标；（1）将矩形ABCD向右平移m个单位，使点A、C恰好同时落在反比例函数（）的图象上，得矩形A′B′C′D′．求矩形ABCD的平移距离m和反比例函数的解析式．   19．（5分）如图①，E是AB延长线上一点，分别以AB、BE为一边在直线AE同侧作正方形ABCD和正方形BEFG，连接AG、CE．  (1)试探究线段AG与CE的大小关系，并证明你的结论；(2)若AG恰平分∠BAC，且BE=1，试求AB的长；(3)将正方形BEFG绕点B逆时针旋转一个锐角后,如图②,问(1)中结论是否仍然成立，说明理由.   20．（8分）如图，在平面直角坐标系中，点A(1，4)，点B(3，2)，连接OA，OB．（1）求直线OB与AB的解析式；（2）求△AOB的面积．（3）下面两道小题，任选一道作答．作答时，请注明题号，若多做，则按首做题计入总分．①在y轴上是否存在一点P，使△PAB周长最小．若存在，请直接写出点P坐标；若不存在，请说明理由．②在平面内是否存在一点C，使以A，O，C，B为顶点的四边形是平行四边形．若存在，请直接写出点C坐标；若不存在，请说明理由．   21．（10分）某公司招聘职员，对甲、乙两位候选人进行了面试和笔试，面试中包括形体和口才，笔试中包括专业水平和创新能力考察，他们的成绩(百分制)如下表：候选人面试笔试形体口才专业水平创新能力甲86909692乙92889593若公司根据经营性质和岗位要求认为：形体、口才、专业水平、创新能力按照4：6：5：5的比确定，请计算甲、乙两人各自的平均成绩，看看谁将被录取？   22．（10分）先化简：，再从中选取一个你认为合适的整数代入求值．   23．（12分）已知，矩形中，，的垂直平分线分别交于点，垂足为．（1）如图1，连接，求证：四边形为菱形；（2）如图2，动点分别从两点同时出发，沿和各边匀速运动一周，即点自停止，点自停止．在运动过程中，①已知点的速度为每秒，点的速度为每秒，运动时间为秒，当四点为顶点的四边形是平行四边形时，则____________．②若点的运动路程分别为 （单位:），已知四点为顶点的四边形是平行四边形，则与满足的数量关系式为____________．           参考答案 一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.1、A2、B3、A4、B5、B6、C7、C8、A9、B10、C11、D12、A 二、填空题（每题4分，满分20分，将答案填在答题纸上）13、214、215、﹣816、；17、1 三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）18、（2）B（，），C（，），D（，）；（2）m=4，．19、（1）AG=CE.，理由见解析；（2）+1；;（3）AG=CE仍然成立，理由见解析；20、（1）直线OB的解析式为，直线AB的解析式为y= -x+1（2）1；（3）①存在，(0，)；②存在，(2，-2)或(4，6)或(-2，2)21、选择乙.22、；当时，原式或当时，原式（任选其一即可）．23、（1）见解析；（2）①；②