山东省泰安市2022-2023学年数学七年级第二学期期末学业质量监测试题含答案

山东省泰安市2022-2023学年数学七年级第二学期期末学业质量监测试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项:

1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内。

2．答题时请按要求用笔。

3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效。

4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。

5．保持卡面清洁，不要折暴、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1．下列关于直线的说法正确的是（     ）

A．经过第一、二、四象限 B．与轴交于点

C．随的增大而减小 D．与轴交于点

2．把分式中、的值都扩大为原来的2倍，分式的值（    ）

A．缩小为原来的一半 B．扩大为原来的2倍

C．扩大为原来的4倍 D．不变

3．正十边形的每一个内角的度数为（   ）

A．120° B．135° C．140° D．144°

4．要使代数式有意义，实数的取值范围是（     ）

A． B． C． D．

5．如图，在△ABC中，AB＝AC，∠BAC＝50°，∠BAC的角平分线AF与AB的垂直平分线DF交于点F，连接CF，BF，则∠BCF的度数为（　　）

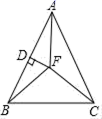
A．30° B．40° C．50° D．45°

6．某种商品的进价为800元，出售时标价为1200元，后来由于该商品积压，商店准备打折销售，但要保证利润率不低于5%，则至多可打（ ）

A．6折 B．7折

C．8折 D．9折

7．某学校改造一个边长为5米的正方形花坛，经规划后，南北方向要缩短x米(0<x<5)，东西方向要加长x米，则改造后花坛的面积与原来的花坛面积相比（   ）

A．增加了x平方米 B．减少了2x平方米

C．保持不变 D．减少了x2平方米

8．绍兴市著名的桥乡，如图，石拱桥的桥顶到水面的距离CD为8m，桥拱半径OC为5m，则水面宽AB为（ ）

A．4m B．5m C．6m D．8m

9．如图，一同学在湖边看到一棵树，他目测出自己与树的距离为20m，树的顶端在水中的倒影距自己5m 远，该同学的身高为1.7m ，则树高为（    ）.　

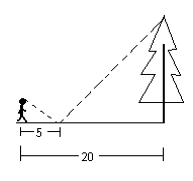
A．3.4m B．4.7 m C．5.1m D．6.8m

10．定义，当时，，当＜时，；已知函数，则该函数的最大值是

A． B． C． D．

11．某校将举办一场“中国汉字听写大赛”，要求每班推选一名同学参加比赛，为此，八年级（1)班组织了五轮班级选拔赛，下表记录了该班甲、乙、丙、丁四名同学五轮选拔赛成绩的平均数与方差S2：根据表中数据，要从中选择一名成绩好又发挥稳定的同学参赛，应该选择（　　）　

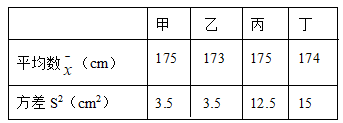
A．甲 B．乙 C．丙 D．丁

12．下面四个手机应用图标中是轴对称图形的是(　  　)

A． B． C． D．

二、填空题（每题4分，满分20分，将答案填在答题纸上）

13．在平行四边形ABCD中，AE平分交边BC于E，DF平分交边BC于F．若，，则_________．

14．将一次函数y=3x﹣1的图象沿y轴向_____平移_____个单位后，得到的图象经过原点．

15．如图，将正五边形 ABCDE 的 C 点固定，并按顺时针方向旋转一定的角度，可使得新五边形A′B′C′D′E′的 顶点 D′落在直线 BC 上，则旋转的角度是______________度.

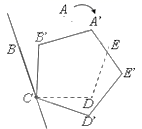
16．某学习小组有5人，在一次数学测验中的成绩分别是102, 106, 100, 105, 102,则他们成绩的平均数_______________

17．对分式，，进行通分时，最简公分母是_____

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18．（5分）如图，在正方形网格中，每个小正方形的边长都是1，点A、B、C、D都在格点上．

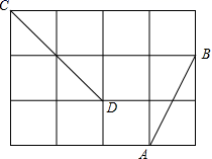
（1）线段AB的长是______；

（2）在图中画出一条线段EF，使EF的长为，并判断AB、CD、EF三条线段的长能否成为一个直角三角形三边的长？说明理由．

19．（5分）已知，求的值.

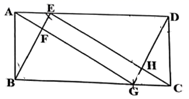
20．（8分）如图，矩形 ABCD 中，AB  4, BC  10, E 在 AD 上，连接 BE, CE, 过点 A 作 AG // CE ，分别交 BC, BE 于点 G, F , 连接 DG 交 CE 于点 H .若 AE  2, 求证：四边形 EFGH 是矩形.

21．（10分）已知四边形ABCD和四边形CEFG都是正方形，且AB＞CE

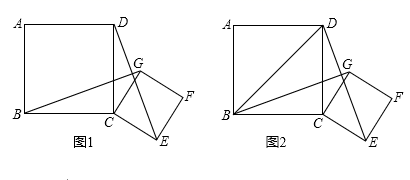
(1) 如图1，连接BG、DE，求证：BG＝DE

(2) 如图2，如果正方形CEFG绕点C旋转到某一位置恰好使得CG∥BD，BG＝BD

① 求∠BDE的度数

② 若正方形ABCD的边长是，请直接写出正方形CEFG的边长____________

22．（10分）已知一次函数的图象经过，两点．

（1）求这个一次函数的解析式；

（2）试判断点是否在这个一次函数的图象上；

（3）求此函数图象与轴，轴围成的三角形的面积．

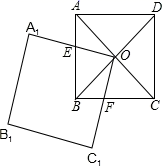
23．（12分）如图，正方形ABCD的对角线AC和BD相交于点O，正方形A1B1C1O的边OA1交AB于点E，OC1交BC于点F．

（1）求证：（BE+BF）2=2OB2；

（2）如果正方形ABCD的边长为a，那么正方形A1B1C1O绕O点转动的过程中，与正方形ABCD重叠部分的面积始终等于　　　　  （用含a的代数式表示）

参考答案

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1、D

2、D

3、D

4、B

5、B

6、B

7、D

8、D

9、C

10、B

11、A

12、D

二、填空题（每题4分，满分20分，将答案填在答题纸上）

13、4或9

14、上    1   

15、1°

16、103

17、8xy1

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18、（1）；（2）见解析，AB、CD、EF三条线段的长能成为一个直角三角形三边的长，理由见解析

19、-.

20、证明见解析.

21、（1）见解析；（2）①∠BDE=60°；②−1.

22、（1）；（2）不在这个一次函数的图象上；（3）函数图象与轴，轴围成的三角形的面积=4.

23、（1）证明见解析；（1）．