


山东省济宁市济宁院附属中学2022-2023学年七下数学期末学业质量监测试题含答案
展开山东省济宁市济宁院附属中学2022-2023学年七下数学期末学业质量监测试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
考生须知:
1.全卷分选择题和非选择题两部分,全部在答题纸上作答。选择题必须用2B铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。
2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。
3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。
一、选择题(每小题3分,共30分)
1.下列命题,①4的平方根是2;②有两边和一角相等的两个三角形全等;③等腰三角形的底角必为锐角;④两组对角分别相等的四边形是平行四边形.其中真命题有( )
A.4个 B.3个 C.2个 D.1个
2.如图,直线l上有三个正方形a,b,c,若a,c的面积分别为5和11,则b的面积为( )
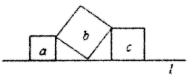
A.6 B.8 C.16 D.55
3.根据如图所示的程序计算函数y的值,若输入的x值是4或7时,输出的y值相等,则b等于( )
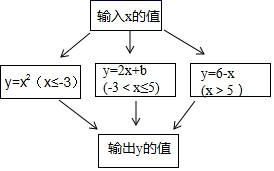
A.9 B.7 C.﹣9 D.﹣7
4.如图是甲、乙两个探测气球所在位置的海拔高度![]() (单位:
(单位:![]() )关于上升时间
)关于上升时间![]() (单位:
(单位:![]() )的函数图像.有下列结论:
)的函数图像.有下列结论:
①当![]() 时,两个探测气球位于同一高度
时,两个探测气球位于同一高度
②当![]() 时,乙气球位置高;
时,乙气球位置高;
③当![]() 时,甲气球位置高;
时,甲气球位置高;
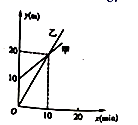
其中,正确结论的个数是( )
A.![]() 个 B.
个 B.![]() 个 C.
个 C.![]() 个 D.
个 D.![]() 个
个
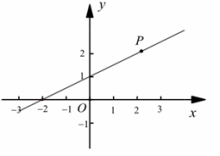
5.如图,已知直线y1=x+a与y2=kx+b相交于点P(﹣1,2),则关于x的不等式x+a>kx+b的解集正确的是( )
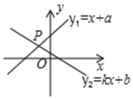
A.x>﹣1 B.x>1 C.x<1 D.x<﹣1
6.如图,△AOB为等腰三角形,顶点A的坐标(2,![]() ),底边OB在x轴上.将△AOB绕点B按顺时针方向旋转一定角度后得△A′O′B,点A的对应点A′在x轴上,则点O′的坐标为( )
),底边OB在x轴上.将△AOB绕点B按顺时针方向旋转一定角度后得△A′O′B,点A的对应点A′在x轴上,则点O′的坐标为( )
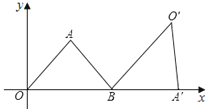
A.(![]() ,
,![]() ) B.(
) B.(![]() ,
,![]() ) C.(
) C.(![]() ,
,![]() ) D.(
) D.(![]() ,4
,4![]() )
)
7.如图,函数y=kx+b(k≠0)的图象经过点B(2,0),与函数y=2x的图象交于点A,则不等式0<kx+b<2x的解集为( )
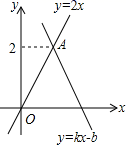
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.在△ABC中,若AB=8,BC=15,AC=17,则AC边上的中线BD的长为( )
A.8 B.8.5 C.9 D.9.5
9.下列函数中,图像不经过第二象限的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.一次函数 y mx ![]() 的图像过点(0,2),且 y 随 x 的增大而增大,则 m 的值为( )
的图像过点(0,2),且 y 随 x 的增大而增大,则 m 的值为( )
A.1 B.3 C.1 D. 1 或 3
二、填空题(本大题共有6小题,每小题3分,共18分)
11.把二次函数y= -2x2-4x-1的图象向上平移3个单位长度,再向右平移4个单位长度,则两次平移后的图象的解析式是 _____________;
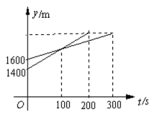
12.某次越野跑中,当小明跑了1600m时,小刚跑了1400m,小明和小刚在此后时间里所跑的路程y(m)与时间t(s)之间的函数关系如图所示,则这次越野跑全程为________ m.
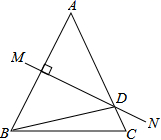
13.如图,等腰△ABC中,AB=AC,∠DBC=15°,AB的垂直平分线MN交AC于点D,则∠A的度数是 .
14.点A(a,b)是一次函数y=x+2与反比例函数![]() 的图像的交点,则
的图像的交点,则![]() __________。
__________。
15.如图,在平面直角坐标系中,点A、B、C的坐标分别是A(﹣2,5),B(﹣3,﹣1),C(1,﹣1),在第一象限内找一点D,使四边形ABCD是平行四边形,那么点D的坐标是_____.
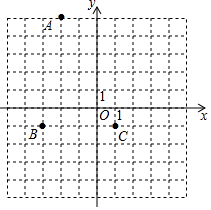
16.已知关于x的方程![]() 有两个不相等的实数根,则a的取值范围是_____________.
有两个不相等的实数根,则a的取值范围是_____________.
三、解下列各题(本大题共8小题,共72分)
17.(8分)对于平面直角坐标系xOy中的点P和正方形给出如下定义:若正方形的对角线交于点O,四条边分别和坐标轴平行,我们称该正方形为原点正方形,当原点正方形上存在点Q,满足PQ≤1时,称点P为原点正方形的友好点.
(1)当原点正方形边长为4时,
①在点P1(0,0),P2(-1,1),P3(3,2)中,原点正方形的友好点是__________;
②点P在直线y=x的图象上,若点P为原点正方形的友好点,求点P横坐标的取值范围;
(2)乙次函数y=-x+2的图象分别与x轴,y轴交于点A,B,若线段AB上存在原点正方形的友好点,直接写出原点正方形边长a的取值范围.
18.(8分)如图,在矩形纸片![]() 中,
中,![]() ,
,![]() .将矩形纸片折叠,使点
.将矩形纸片折叠,使点![]() 与点
与点![]() 重合,求折痕
重合,求折痕![]() 的长.
的长.
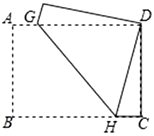
19.(8分)已知:将矩形![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到矩形
得到矩形![]() .
.
(1)如图![]() ,当点
,当点![]() 在
在![]() 上时,求证:
上时,求证:![]()
(2)当旋转角![]() 的度数为多少时,
的度数为多少时,![]() ?
?
(3)若![]() ,请直接写出在旋转过程中
,请直接写出在旋转过程中![]() 的面积的最大值.
的面积的最大值.
20.(8分)如图,正比例函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点,其中点
两点,其中点![]() 的横坐标为
的横坐标为![]() .
.
(1)求![]() 的值.
的值.
(2)若点![]() 是
是![]() 轴上一点,且
轴上一点,且![]() ,求点
,求点![]() 的坐标.
的坐标.
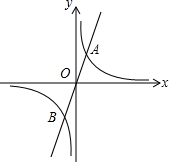
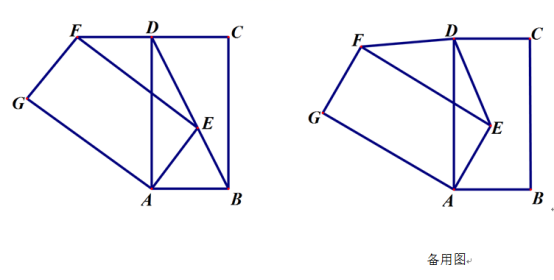
21.(8分)如图,边长为2的正方形纸片ABCD中,点M为边CD上一点(不与C,D重合),将△ADM沿AM折叠得到△AME,延长ME交边BC于点N,连结AN.
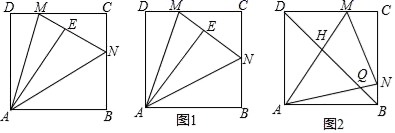
(1)猜想∠MAN的大小是否变化,并说明理由;
(2)如图1,当N点恰为BC中点时,求DM的长度;
(3)如图2,连结BD,分别交AN,AM于点Q,H.若BQ=![]() ,求线段QH的长度.
,求线段QH的长度.
22.(10分)如图,方格纸中每个小正方形的边长都是1个单位长度,![]() 的三个顶点
的三个顶点![]() ,
,![]() ,
,![]() .
.
(1)将![]() 以点
以点![]() 为旋转中心旋转
为旋转中心旋转![]() ,得到△
,得到△![]() ,请画出△
,请画出△![]() 的图形;
的图形;
(2)平移![]() ,使点
,使点![]() 的对应点
的对应点![]() 坐标为
坐标为![]() ,请画出平移后对应的△
,请画出平移后对应的△![]() 的图形;
的图形;
(3)若将△![]() 绕某一点旋转
绕某一点旋转![]() 可得到△
可得到△![]() ,请直接写出旋转中心的坐标.
,请直接写出旋转中心的坐标.
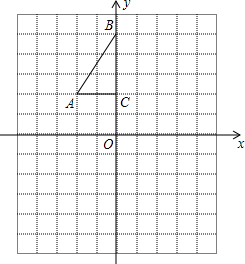
23.(10分)如图,在直角坐标平面内,直线y=﹣![]() x﹣4与x轴、y轴分别交于点A、B,点C在x轴正半轴上,且满足OC=
x﹣4与x轴、y轴分别交于点A、B,点C在x轴正半轴上,且满足OC=![]() OB.
OB.
(1)求线段AB的长及点C的坐标;
(2)设线段BC的中点为E,如果梯形AECD的顶点D在y轴上,CE是底边,求点D的坐标和梯形AECD的面积.
24.(12分)如图,在平面直角坐标系中,直线![]() 与直线
与直线![]() 相交于点 A .
相交于点 A .
(I)求直线![]() 与 x 轴的交点坐标,并在坐标系中标出点 A 及画出直线
与 x 轴的交点坐标,并在坐标系中标出点 A 及画出直线 ![]() 的图象;
的图象;
(II)若点P是直线![]() 在第一象限内的一点,过点P作 PQ//y 轴交直线
在第一象限内的一点,过点P作 PQ//y 轴交直线 ![]() 于点Q,△POQ 的面积等于60 ,试求点P 的横坐标.
于点Q,△POQ 的面积等于60 ,试求点P 的横坐标.
参考答案
一、选择题(每小题3分,共30分)
1、C
2、C
3、C
4、D
5、A
6、C
7、A
8、B
9、B
10、B
二、填空题(本大题共有6小题,每小题3分,共18分)
11、y= -2x2+12x-2
12、1
13、50°.
14、-8
15、(2,5).
16、![]() 且
且![]()
三、解下列各题(本大题共8小题,共72分)
17、(1)①P2,P3 ,②1≤x≤![]() 或
或![]() ≤x≤-1;(2)2-
≤x≤-1;(2)2-![]() ≤a≤1.
≤a≤1.
18、![]() .
.
19、(1)详见解析;(2)当旋转角![]() 的度数为
的度数为![]() 时,
时,![]() ;(3)
;(3)![]()
20、(1)k=2;(2)P点的坐标为![]() 或
或![]() .
.
21、(1)∠MAN的大小没有变化,理由见解析;(2)![]() ;(3)
;(3)![]() .
.
22、 (1)见解析;(2)见解析;(3)旋转中心坐标![]() .
.
23、(1)A(﹣3,0),B(0,﹣4),C(2,0);(2)S梯形AECD=1.
24、 (I)见解析;(II) 点![]() 的横坐标为12.
的横坐标为12.
山东省济宁市金乡县2022-2023学年七下数学期末学业质量监测模拟试题含答案: 这是一份山东省济宁市金乡县2022-2023学年七下数学期末学业质量监测模拟试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,计算等内容,欢迎下载使用。
山东省济宁市兖州区2022-2023学年七下数学期末监测试题含答案: 这是一份山东省济宁市兖州区2022-2023学年七下数学期末监测试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,P1,如图所示,在中,,则为等内容,欢迎下载使用。
山东省济宁市2022-2023学年七下数学期末学业质量监测模拟试题含答案: 这是一份山东省济宁市2022-2023学年七下数学期末学业质量监测模拟试题含答案,共8页。试卷主要包含了下列命题正确的是,下面有四个定理,已知P1,定义新运算等内容,欢迎下载使用。












