


2022-2023学年山东省济宁院附中数学七下期末综合测试模拟试题含答案
展开2022-2023学年山东省济宁院附中数学七下期末综合测试模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项
1.考试结束后,请将本试卷和答题卡一并交回.
2.答题前,请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置.
3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符.
4.作答选择题,必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选涂其他答案.作答非选择题,必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效.
5.如需作图,须用2B铅笔绘、写清楚,线条、符号等须加黑、加粗.
一、选择题(每小题3分,共30分)
1.如图,在R△ABC中,∠C=90°,∠A=30°,BC=4cm,则AB等于( )
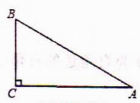
A.9 cm B.8 cm C.7cm D.6cm
2.下列计算中,①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 不正确的有( )
不正确的有( )
A.3个 B.2个 C.1个 D.4个
3.通过估算,估计![]() 的大小应在( )
的大小应在( )
A.7~8之间 B.8.0~8.5之间
C.8.5~9.0之间 D.9~10之间
4.在平行四边形ABCD中,∠BAD=110°,∠ABD=30°,则∠CBD度数为( )
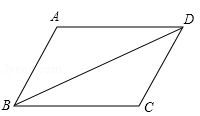
A.30° B.40° C.70° D.50°
5.如图,将矩形纸片![]() 按如下步骤操作:将纸片对折得折痕
按如下步骤操作:将纸片对折得折痕![]() ,折痕与
,折痕与![]() 边交于点
边交于点![]() ,与
,与![]() 边交于点
边交于点![]() ;将矩形
;将矩形![]() 与矩形
与矩形![]() 分别沿折痕
分别沿折痕![]() 和
和![]() 折叠,使点
折叠,使点![]() ,点
,点![]() 都与点
都与点![]() 重合,展开纸片,恰好满足
重合,展开纸片,恰好满足![]() .则下列结论中,正确的有( )
.则下列结论中,正确的有( )
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .
.
A.4个 B.3个 C.2个 D.1个
6.用反证法证明命题:“四边形中至少有一个角是钝角或直角”时,首先应该假设这个四边形中( )
A.有一个角是钝角或直角 B.每一个角都是钝角
C.每一个角都是直角 D.每一个角都是锐角
7.上周周末放学,小华的妈妈来学校门口接他回家,小华离开教室后不远便发现把文具盒遗忘在了教室里,于是以相同的速度折返回去拿,到了教室后碰到班主任,并与班主任交流了一下周末计划才离开,为了不让妈妈久等,小华快步跑到学校门口,则小华离学校门口的距离y与时间t之间的函数关系的大致图象是( )
A.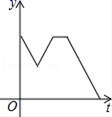 B.
B.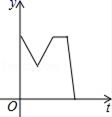 C.
C.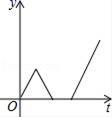 D.
D.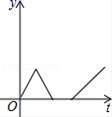
8.在□![]() 中,
中,![]() ,则
,则![]() 的度数为( )
的度数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.某航空公司规定,旅客乘机所携带行李的质量x(kg)与其运费y(元)由如图所示的一次函数图象确定,那么旅客可携带的免费行李的最大质量为( )
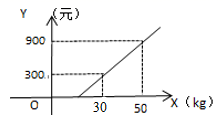
A.20kg B.25kg C.28kg D.30kg
10.已知一次函数y1=2x+m与y2=2x+n(m≠n)的图象如图所示,则关于x与y的二元一次方程组 ![]() 的解的个数为( )
的解的个数为( )
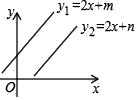
A.0个 B.1个 C.2个 D.无数个
二、填空题(本大题共有6小题,每小题3分,共18分)
11.若点P(-2,2)是正比例函数y=kx(k≠0)图象上的点,则此正比例函数的解析式为______.
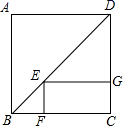
12.如图,E是正方形ABCD的对角线BD上任意一点,四边形EGCG是矩形,若正方形ABCD的周长为a,则矩形EFCG的周长为_______________.
13.如图,在Rt△ABC中,∠ACB=90°,AC=BC=6cm,动点P从点A出发,沿AB方向以每秒![]() cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒lcm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′,设Q点运动的时间为t秒,若四边形QP′CP为菱形,则t的值为_____.
cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒lcm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′,设Q点运动的时间为t秒,若四边形QP′CP为菱形,则t的值为_____.

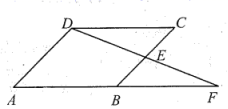
14.如图,在四边形![]() 中,
中, ![]() 是
是![]() 边的中点,连接
边的中点,连接![]() 并延长,交
并延长,交![]() 的延长线与
的延长线与![]() 点,
点, ![]() ,请你添加一个条件(不需要添加任何线段或字母),使之能推出四边形
,请你添加一个条件(不需要添加任何线段或字母),使之能推出四边形![]() 为平行四边形,你添加的条件是_________,并给予证明.
为平行四边形,你添加的条件是_________,并给予证明.
15.在平面直角坐标系xOy中,点A(2,﹣3)关于x轴对称的点B的坐标是______.
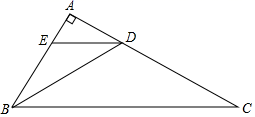
16.如图,在Rt△ABC中,BD平分∠ABC交AC于点D,过D作DE∥BC交AB于点E,若DE刚好平分∠ADB,且AE=a,则BC=_____.
三、解下列各题(本大题共8小题,共72分)
17.(8分)如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE
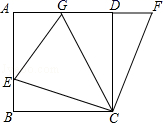
(1)求证:CE=CF;
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
18.(8分)计算:
(1)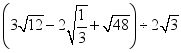
(2)![]()
(3)先化简:再求值.![]() ,其中
,其中![]()
19.(8分)(1)发现规律:
特例1:![]() =
=![]() =
=![]() =
=![]() ;
;
特例2:![]() =
=![]() =
=![]() =
=![]() ;
;
特例3:![]() =4
=4![]() ;
;
特例4:______(填写一个符合上述运算特征的例子);
(2)归纳猜想:
如果n为正整数,用含n的式子表示上述的运算规律为:______;
(3)证明猜想:
(4)应用规律:
①化简:![]() ×
×![]() =______;
=______;
②若![]() =19
=19![]() ,(m,n均为正整数),则m+n的值为______.
,(m,n均为正整数),则m+n的值为______.
20.(8分)为响应国家全民阅读的号召,某社区鼓励居民到社区阅览室借阅读书,并统计每年的借阅人数和图书借阅总量(单位:本),该阅览室在2014年图书借阅总量是7500本,2016年图书借阅总量是10800本.
(1)求该社区的图书借阅总量从2014年至2016年的年平均增长率;
(2)已知2016年该社区居民借阅图书人数有1350人,预计2017年达到1440人,如果2016年至2017年图书借阅总量的增长率不低于2014年至2016年的年平均增长率,那么2017年的人均借阅量比2016年增长a%,求a的值至少是多少?
21.(8分)某校为了解八年级男生立定跳远测试情况,随机抽取了部分八年级男生的测试成绩进行统计,根据评分标准,将他们的成绩分为优秀、良好、及格、不及格四个等级,以下是根据调查结果绘制的统计图表的一部分.
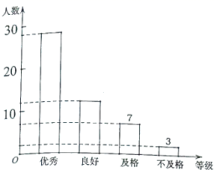
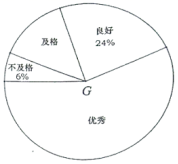
根据以上信息,解答下列问题:
(1)被调查的男生中,成绩等级为不及格的男生人数有__________人,成绩等级为良好的男生人数占被调查男生人数的百分比为__________%;
(2)被调查男生的总数为__________人,条形统计图中优秀的男生人数为__________人;
(3)若该校八年级共有300名男生,根据调查结果,估计该校八年级男生立定跳远测试成绩为良好和优秀的男生人数.
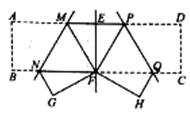
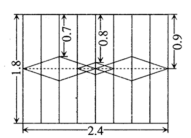
22.(10分)某工人为一客户制作一长方形防盗窗,为了牢固和美观,设计如图所示,中间为三个菱形,其中左右为两个全等的大菱形,中间为一个小菱形,竖着的铁棍的间距是相等的,尺寸如图所示(单位:m),工人师傅要做这样的一个防盗窗,总共需要多长的铁棍(不计损耗?)
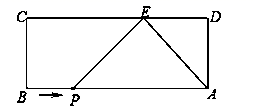
23.(10分)如图,矩形ABCD中,AB=9,AD=4. E为CD边上一点,CE=6. 点P从点B出发,以每秒1个单位的速度沿着边BA向终点A运动,连接PE.设点P运动的时间为t秒.
(1)求AE的长;
(2)当t为何值时,△PAE为直角三角形;
(3)是否存在这样的t,使EA恰好平分∠PED,若存在,求出t的值;若不存在,请说明理由.
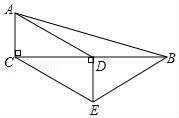
24.(12分)如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE∥AD.
(1)求证:四边形ACED是平行四边形;
(2)若AC=2,CE=4,求四边形ACEB的周长.
参考答案
一、选择题(每小题3分,共30分)
1、B
2、A
3、C
4、B
5、B
6、D
7、B
8、B
9、A
10、A
二、填空题(本大题共有6小题,每小题3分,共18分)
11、y=-x
12、![]()
13、1
14、添加的条件是:∠F=∠CDE
15、(2,3)
16、6a
三、解下列各题(本大题共8小题,共72分)
17、(1)见解析(2)成立
18、(1)![]() ;(2)9;(3)
;(2)9;(3)![]() .
.
19、(1)![]() ;(2)
;(2)![]() ;(3)见解析;(4)①2121
;(3)见解析;(4)①2121![]() ;②m+n=2
;②m+n=2
20、(1)20%;(2)12.1.
21、(1)3,24;(2)50,28;(3)估计该校八年级男生立定跳远测试成绩在良好以上的男生人数为240人.
22、需要![]() m的铁棍.
m的铁棍.
23、(1)5;(2)6或![]() ;(3)存在,t=
;(3)存在,t=![]() ,理由见解析
,理由见解析
24、(1)详见解析;(1)10+1![]() .
.
山东省济宁院附中2023-2024学年数学九上期末质量检测模拟试题含答案: 这是一份山东省济宁院附中2023-2024学年数学九上期末质量检测模拟试题含答案,共7页。试卷主要包含了关于二次函数,下列说法正确的是等内容,欢迎下载使用。
山东省济宁汶上县联考2022-2023学年数学七下期末综合测试模拟试题含答案: 这是一份山东省济宁汶上县联考2022-2023学年数学七下期末综合测试模拟试题含答案,共6页。试卷主要包含了已知,若,则的值是等内容,欢迎下载使用。
山东省济宁市济宁院附属中学2022-2023学年七下数学期末学业质量监测试题含答案: 这是一份山东省济宁市济宁院附属中学2022-2023学年七下数学期末学业质量监测试题含答案,共8页。试卷主要包含了如图,函数y=kx+b等内容,欢迎下载使用。












