


山东省德州市庆云二中学2022-2023学年七年级数学第二学期期末达标检测试题含答案
展开山东省德州市庆云二中学2022-2023学年七年级数学第二学期期末达标检测试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
考生请注意:
1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。
2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。
3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
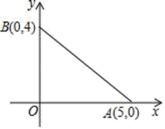
1.如图,在平面直角坐标系中有两点A(5,0),B(0,4),则它们之间的距离为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.菱形具有而矩形不一定具有的性质是 ( )
A.对角线互相垂直 B.对角线相等 C.对角线互相平分 D.对角互补
3.若使二次根式![]() 在实数范围内有意义,则
在实数范围内有意义,则![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.若a>b,则下列各式不成立的是( )
A.a﹣1>b﹣2 B.5a>5b C.﹣![]() a>﹣
a>﹣![]() b D.a﹣b>0
b D.a﹣b>0
5.使用同一种规格的下列地砖,不能进行平面镶嵌的是( )
A.正三角形地砖 B.正四边形地砖 C.正五边形地砖 D.正六边形地砖
6.在![]() 中,
中,![]() ,
,![]() 是对角线
是对角线![]() 上的两点(不与点
上的两点(不与点![]() ,
,![]() 重合)下列条件中,无法判断四边形
重合)下列条件中,无法判断四边形![]() 一定为平行四边形的是( )
一定为平行四边形的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.为了研究特殊四边形,李老师制作了这样一个教具(如图1):用钉子将四根木条钉成一个平行四边形框架ABCD,并在A与C、B与D两点之间分别用一根橡皮筋拉直固定,课上,李老师右手拿住木条BC,用左手向右推动框架至AB⊥BC(如图2)观察所得到的四边形,下列判断正确的是( )
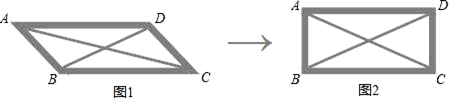
A.∠BCA=45° B.AC=BD
C.BD的长度变小 D.AC⊥BD
8.如图,![]() 由
由![]() 绕
绕![]() 点旋转
点旋转![]() 而得到,则下列结论不成立的是( )
而得到,则下列结论不成立的是( )
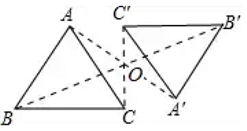
A.点![]() 与点
与点![]() 是对应点 B.
是对应点 B.![]()
C.![]() D.
D.![]()
9.如图,在平面直角坐标系中,直线y=-3x+3与坐标轴分别交于A,B两点,以线段AB为边,在第一象限内作正方形ABCD,直线y=3x-2与y轴交于点F,与线段AB交于点E,将正方形ABCD沿x轴负半轴方向平移a个单位长度,使点D落在直线EF上.有下列结论:①△ABO的面积为3;②点C的坐标是(4,1);③点E到x轴距离是![]() ;
;
④a=1.其中正确结论的个数是( )
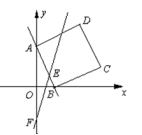
A.4个 B.3个 C.2个 D.1个
10.下列4个命题:
①对角线相等且互相平分的四边形是正方形;
②有三个角是直角的四边形是矩形;
③对角线互相垂直的平行四边形是菱形;
④一组对边平行,另一组对边相等的四边形是平行四边形
其中正确的是( )
A.②③ B.② C.①②④ D.③④
11.如图,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上一点,连接
边上一点,连接![]() ,把
,把![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在点
落在点![]() 处,当
处,当![]() 为直角三角形时,
为直角三角形时,![]() 的长为( )
的长为( )
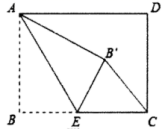
A.3 B.![]() C.2或3 D.3或
C.2或3 D.3或![]()
12.二次根式![]() 有意义的条件是( )
有意义的条件是( )
A.x<2 B.x<﹣2 C.x≥﹣2 D.x≤2
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13.如图所示,△ABC是边长为20的等边三角形,点D是BC边上任意一点,DE⊥AB于点E,DF⊥AC于点F,则BE+CF=____________.
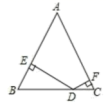
14.如图,在![]() 中,
中,![]() ,将
,将![]() 绕顶点
绕顶点![]() 顺时针旋转,旋转角为
顺时针旋转,旋转角为![]() ,得到
,得到![]() .设
.设![]() 中点为
中点为![]() ,
,![]() 中点为
中点为![]() ,
,![]() ,连接
,连接![]() ,当
,当![]() ____________
____________![]() 时,
时,![]() 长度最大,最大值为____________.
长度最大,最大值为____________.
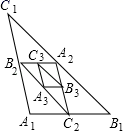
15.如图,△A1B1C1中,A1B1=4,A1C1=5,B1C1=1.点A2,B2,C2分别是边B1C1,A1C1,A1B1的中点;点A3,B3,C3分别是边B2C2,A2C2,A2B2的中点;…;以此类推,则第2019个三角形的周长是_____.
16.若x-y=![]() ,xy=
,xy=![]() ,则代数式(x-1)(y+1)的值等于_____.
,则代数式(x-1)(y+1)的值等于_____.
17.已知一组数据1,2,0,﹣1,x,1的平均数是1,那么这组数据的方差是__.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
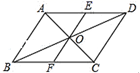
18.(5分)如图,在▱ABCD 中,对角线 AC,BD 相交于点 O,过点 O 的一条直线分别交 AD,BC 于点 E,F.求证:AE=CF.
19.(5分)已知函数y=x+![]() (x>0),它的图象犹如老师的打钩,因此人称对钩函数.下表是y与x的几组对应值:
(x>0),它的图象犹如老师的打钩,因此人称对钩函数.下表是y与x的几组对应值:
x |
|
|
| 1 | 2 | 3 | 4 |
y | 4 | 3 | 2 | 2 | 2 | 3 | 4 |
请你根据学习函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行探究.
(1)如图,在平面直角坐标系xOy中,描出了上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
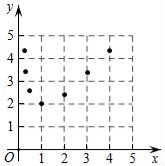
(2)根据画出的函数图象特征,仿照示例,完成下列表格中的函数变化规律:
序号 | 函数图象特征 | 函数变化规律 |
示例1 | 在直线x=1右侧,函数图象呈上升状态 | 当x>1时,y随x的增大而增大 |
示例2 | 函数图象经过点(2,2 | 当x=2时,y=2 |
① | 函数图象的最低点是(1,2) |
|
② | 在直线x=1左侧,函数图象呈下降状态 |
|
(3)当a≤x≤4时,y的取值范围为2≤y≤4![]() ,则a的取值范围为 .
,则a的取值范围为 .
20.(8分)(1)计算:![]()
(2)解方程: (2 x 1)( x 3) 4
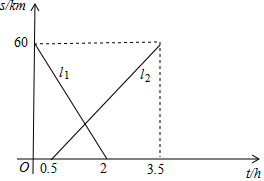
21.(10分)A,B两地相距60km,甲、乙两人从两地出发相向而行,甲先出发.图中l1,l2表示两人离A地的距离s(km)与时间t(h)的关系,请结合图象解答下列问题:
(1)表示乙离A地的距离与时间关系的图象是 (填l1或l2);甲的速度是 km/h,乙的速度是 km/h;
(2)求出l1,l2的解析式,并标注自变量的取值范围。
22.(10分)为深入践行总书记提出的“绿水青山就是金山银山”的重要理念,某学校积极响应号召,进行校园绿化,计划购进![]() 、
、![]() 两种树苗共30棵,已知
两种树苗共30棵,已知![]() 种树苗每棵80元,
种树苗每棵80元,![]() 种树苗每棵50元.设购买
种树苗每棵50元.设购买![]() 种树苗
种树苗![]() 棵,购买两种树苗所需费用为
棵,购买两种树苗所需费用为![]() 元
元
(1)求![]() 与
与![]() 的函数关系式.
的函数关系式.
(2)若购买![]() 种树苗的数量不少于
种树苗的数量不少于![]() 种树苗数量的2倍,请给出一种费用最少的购买方案,并求出该方案所需的费用.
种树苗数量的2倍,请给出一种费用最少的购买方案,并求出该方案所需的费用.
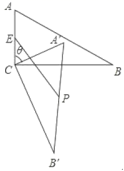
23.(12分)如图,以矩形![]() 的顶点
的顶点![]() 为坐标原点,
为坐标原点,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,建立平面直角坐标系.已知,
轴,建立平面直角坐标系.已知,![]() ,
,![]() ,点
,点![]() 为
为![]() 轴上一动点,以
轴上一动点,以![]() 为一边在
为一边在![]() 右侧作正方形
右侧作正方形![]() .
.
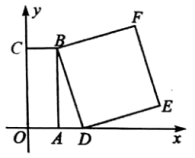
(1)若点![]() 与点
与点![]() 重合,请直接写出点
重合,请直接写出点![]() 的坐标.
的坐标.
(2)若点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() ,求点
,求点![]() 的坐标.
的坐标.
(3)若![]() ,求点
,求点![]() 的坐标.
的坐标.
参考答案
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、A
2、A
3、A
4、C
5、C
6、B
7、B
8、C
9、B
10、A
11、D
12、C
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13、10
14、![]() 3
3
15、![]()
16、2![]() -2
-2
17、![]()
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18、证明见解析.
19、(1)画图见解析;(2):x=1时,y有最小值2,当x<1时,y随x的增大而减小;(3)1≤a≤4
20、(1)![]() ;(2)
;(2)![]() ,
,![]() .
.
21、(1)l2,30,20;(2)l1:s=-30t+60(0≤t≤2),l2:s=20t-10(0.5≤t≤3.5)
22、(1)![]() ;(2)购买
;(2)购买![]() 种树苗20棵,
种树苗20棵,![]() 种树苗10棵费用最少,所需费用为2100元
种树苗10棵费用最少,所需费用为2100元
23、(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,
,![]() .
.
2023-2024学年山东省德州市庆云二中学数学九上期末复习检测模拟试题含答案: 这是一份2023-2024学年山东省德州市庆云二中学数学九上期末复习检测模拟试题含答案,共8页。试卷主要包含了下列命题正确的是,如图,空心圆柱的俯视图是,若,设,,,则、、的大小顺序为,如图所示,该几何体的俯视图是等内容,欢迎下载使用。
山东省德州市庆云县后张中学2022-2023学年七年级下学期第二次月考数学试题: 这是一份山东省德州市庆云县后张中学2022-2023学年七年级下学期第二次月考数学试题,共5页。
山东省德州市夏津实验中学2022-2023学年七下数学期末达标检测模拟试题含答案: 这是一份山东省德州市夏津实验中学2022-2023学年七下数学期末达标检测模拟试题含答案,共6页。试卷主要包含了武汉市光谷实验中学九,下列命题中,假命题是等内容,欢迎下载使用。












