山东省乐陵市实验中学2022-2023学年数学七年级第二学期期末达标检测试题含答案

山东省乐陵市实验中学2022-2023学年数学七年级第二学期期末达标检测试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项：

1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。回答非选择题时，将答案写在答题卡上，写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交回。

一、选择题(每小题3分,共30分)

1．如图所示，已知点C(1，0)，直线与两坐标轴分别交于A，B两点，D，E分别是线段AB，OA上的动点，则△CDE的周长的最小值是(    )

A． B．10

C． D．12

2．已知平行四边形ABCD，下列条件中，不能判定这个平行四边形为矩形的是（　　）

A．∠A=∠B B．∠A=∠C C．AC=BD D．AB⊥BC

3．等腰三角形的一个外角为140°，那么底角等于（   ）

A．40°    B．100°                         C．70°                         D．40°或70°

4．如图，已知直线l1：y＝3x+1和直线l2：y＝mx+n交于点P（a，﹣8），则关于x的不等式3x+1＜mx+n的解集为（   ）

A．x＞﹣3 B．x＜﹣3 C．x＜﹣8 D．x＞﹣8

5．下列根式中属于最简二次根式的是（    ）

A． B． C． D．

6．在平面直角坐标系中，点P（﹣3，2）关于x轴的对称点的坐标为（　　）

A．（2，﹣3）    B．（﹣2，3）    C．（﹣3，2）    D．（﹣3，﹣2）

7．我市某中学举办了一次以“我的中国梦”为主题的演讲比赛，最后确定名同学参加决赛，他们的决赛成绩各不相同，其中小辉已经知道自己的成绩，但能否进前名，他还必须清楚这名同学成绩的（    ）

A．众数 B．平均数 C．方差 D．中位数

8．下列各组数据中,能做为直角三角形三边长的是（    ）。

A．1、2、3 B．3、5、7 C．32，42，52 D．5、12、13

9．如图，在中，，，，延长到点，使，交于点，在上取一点，使，连接．有以下结论：①平分；②；③是等边三角形；④，则正确的结论有（  ）

A．1个 B．2个 C．3个 D．4个

10．在一次体育测试中，小芳所在小组8人的成绩分别是：46，47，48，48，49，49，49，1．则这8人体育成绩的中位数是（    ）

A．47 B．48.5 C．49 D．49.5

二、填空题(本大题共有6小题，每小题3分，共18分)

11．在一次函数y＝kx+b（k≠0）中，函数y与自变量x的部分对应值如表：

则m的值为_____．

12．设是满足不等式的正整数，且关于的二次方程的两根都是正整数，则正整数的个数为_______．

13．在平行四边形ABCD中，若∠A+∠C=140°，则∠B=        ．

14．已知一次函数的图象经过第一、二、四象限，则的取值范围是_____．

15．已知的顶点坐标分别是，，．过点的直线与相交于点．若分的面积比为，则点的坐标为________．

16．某公司测试自动驾驶技术,发现移动中汽车“”通信中每个数据包传输的测量精度大约为0.0000018秒，请将数据0.0000018用科学计数法表示为__________．

三、解下列各题(本大题共8小题，共72分)

17．（8分）（1）操作思考：如图1，在平面直角坐标系中，等腰Rt△ACB的直角顶点C在原点，将其绕着点O旋转，若顶点A恰好落在点（1，2）处．则①OA的长为                    ；②点B的坐标为                    （直接写结果）；

（2）感悟应用：如图2，在平面直角坐标系中，将等腰Rt△ACB如图放置，直角顶点

C(-1,0)，点A(0，4)，试求直线AB的函数表达式；

（3）拓展研究：如图3，在平面直角坐标系中，点B（4；3），过点B作BAy轴，垂足为点A；作BCx轴，垂足为点C，P是线段BC上的一个动点，点Q是直线上一动点．问是否存在以点P为直角顶点的等腰Rt△APQ，若存在，请求出此时P的坐标，若不存在，请说明理由．

18．（8分）如图，矩形ABCD中，AB=2，BC=5，E、P分别在AD、BC上，且DE=BP=1．

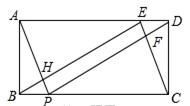
（1）断⊿BEC的形状，并说明理由；

（2）判断四边形EFPH是什么特殊四边形？并证明你的判断．

19．（8分）求不等式（2x﹣1）（x+1）＞0的解集．

解：根据“同号两数相乘，积为正”可得：①或 ②．

解①得x＞；解②得x＜﹣1．

∴不等式的解集为x＞或x＜﹣1．

请你仿照上述方法解决下列问题：

（1）求不等式（2x﹣1）（x+1）＜0的解集．

（2）求不等式≥0的解集．

20．（8分）如图，在平面直角坐标系中，△ABC各顶点的坐标分别为A(−2，−2)，B(−4，−1），C(−4，−4)．

（1）作出ABC关于原点O成中心对称的A1B1C1.

（2）作出点A关于x轴的对称点A'若把点A'向右平移a个单位长度后落在A1B1C1的内部（不包括顶点和边界），求a的取值范围.

21．（8分）如图1,在中,,,、分别是、边上的高,、交于点,连接.

(1)求证:；

(2)求的度数；

(3)如图2,过点作交于点,探求线段、、的数量关系,并说明理由.

22．（10分）如图，正方形网格中的每个小正方形边长都是 1，每个小格的顶点叫做格点， 以格点为顶点分别按下列要求画三角形．

（1）在图 1 中，画一个三角形，使它的三边长都是有理数；

（2）在图 2 中，画一个直角三角形，使它们的直角边都是无理数；

（3）在图 3 中，画一个正方形，使它的面积是 1．

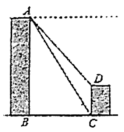
23．（10分）如图，甲、乙两座建筑物的水平距离为，从甲的顶部处测得乙的顶部处的俯角为48°，测得底部处的俯角为58°，求乙建筑物的高度.（参考数据：，，，.结果取整数）

24．（12分）如图，、分别为的边、的中点，，延长至点，使得，连接、、.若时，求四边形的周长.

参考答案

一、选择题(每小题3分,共30分)

1、B

2、B

3、D

4、B

5、A

6、D

7、D

8、D

9、D

10、B

二、填空题(本大题共有6小题，每小题3分，共18分)

11、-2

12、1个．

13、110°

14、

15、（5，-）或（5，-）．

16、

三、解下列各题(本大题共8小题，共72分)

17、（1），（2）（3），

18、（1）△BEC是直角三角形，理由见解析；

（2）四边形EFPH为矩形，证明见解析；

19、（1）﹣1＜x＜；（2）x≥1或x＜﹣2．

20、见解析

21、（1）证明见详解；（2）45°；（3）BC+BE=2BG，理由见详解.

22、（1）见解析（2）见解析（3）见解析

23、38m.

24、四边形的周长为8.