

安徽省合肥市北城片区2022-2023学年数学七下期末考试模拟试题含答案
展开安徽省合肥市北城片区2022-2023学年数学七下期末考试模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
请考生注意:
1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。
2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。
一、选择题(每小题3分,共30分)
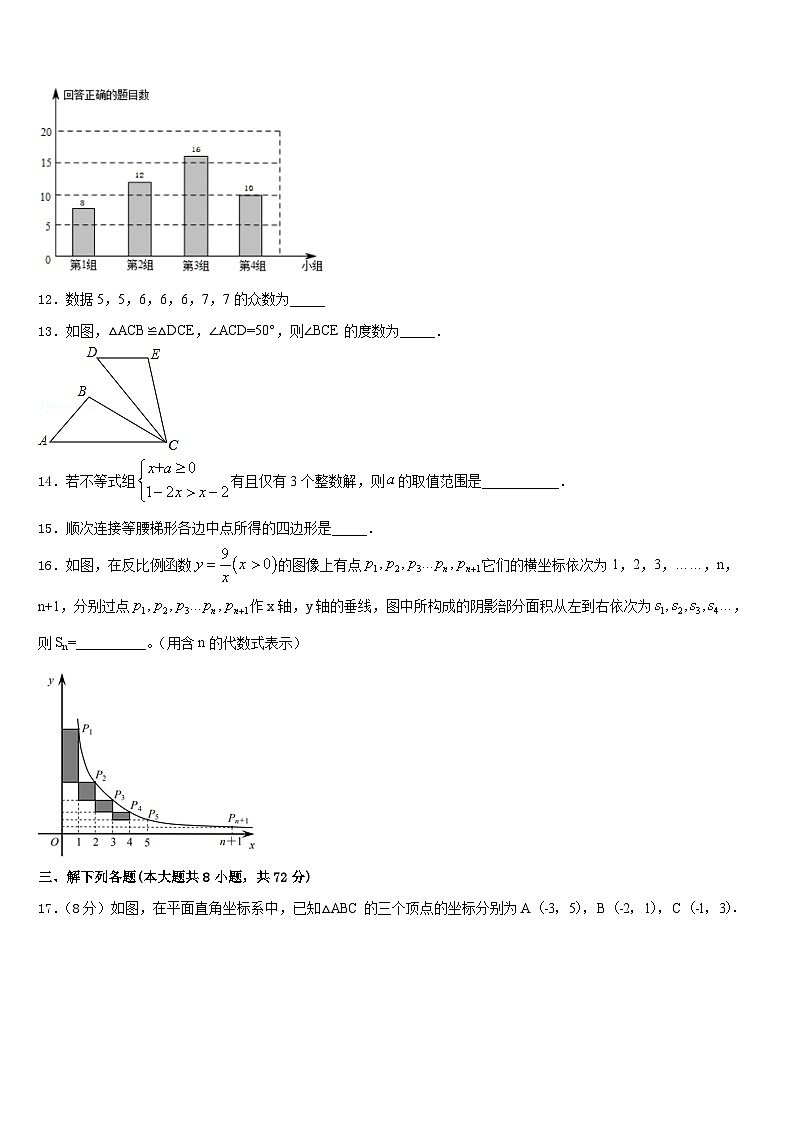
1.甲、乙两人分别骑自行车和摩托车从A地到B地,两人所行驶的路程与时间的关系如图所示,下面的四个说法:
![]() 甲比乙早出发了3小时;
甲比乙早出发了3小时;![]() 乙比甲早到3小时;
乙比甲早到3小时;![]() 甲、乙的速度比是5:6;
甲、乙的速度比是5:6;![]() 乙出发2小时追上了甲.
乙出发2小时追上了甲.
其中正确的个数是![]()
![]()
A.1个 B.2个 C.3个 D.4个
2.已知![]() 是关于
是关于![]() 的方程
的方程![]() 的两个实数根,且满足
的两个实数根,且满足![]() ,则
,则![]() 的值为( )
的值为( )
A.3 B.3或![]() C.2 D.0或2
C.2 D.0或2
3.下列地铁标志图形中,属于中心对称图形的是( )
A.![]() B.
B. C.
C. D.
D.
4.下列命题的逆命题能成立的有( )
①两条直线平行,内错角相等;②如果两个实数相等,那么它们的绝对值相等;③全等三角形的对应角相等;④在角的内部,到角的两边距离相等的点在角的平分线上.
A.4个 B.3个 C.2个 D.1个
5.因式分解x2﹣9y2的正确结果是( )
A.(x+9y)(x﹣9y)
B.(x+3y)(x﹣3y)
C.(x﹣3y)2
D.(x﹣9y)2
6.函数y=![]() 的自变量x的取值范围是( )
的自变量x的取值范围是( )
A.x≥0且x≠2 B.x≥0 C.x≠2 D.x>2
7.下列各组线段a、b、c中不能组成直角三角形的是( )
A.a=8,b=15,c=17 B.a=7,b=24,c=25
C.a=40,b=50,c=60 D.a=![]() ,b=4,c=5
,b=4,c=5
8.关于![]() 的方程
的方程![]() 有实数根,则整数
有实数根,则整数![]() 的最大值是( )
的最大值是( )
A.6 B.7 C.8 D.9
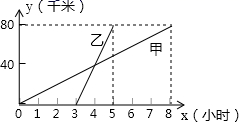
9.如图,周长为34的矩形ABCD被分成7个全等的矩形,则矩形ABCD的面积为
( )
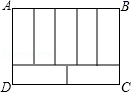
A.280 B.140 C.70 D.196
10.如图,点A,B分别在函数y=![]() (k1>0)与函数y=
(k1>0)与函数y=![]() (k2<0)的图象上,线段AB的中点M在x轴上,△AOB的面积为4,则k1﹣k2的值为( )
(k2<0)的图象上,线段AB的中点M在x轴上,△AOB的面积为4,则k1﹣k2的值为( )
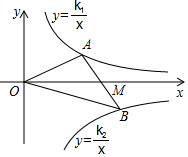
A.2 B.4 C.6 D.8
二、填空题(本大题共有6小题,每小题3分,共18分)
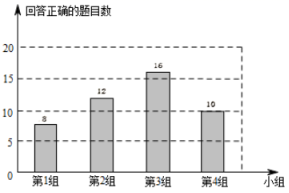
11.在一次智力抢答比赛中,四个小组回答正确的情况如下图.这四个小组平均正确回答__________道题目?(结果取整数)
12.数据5,5,6,6,6,7,7的众数为_____
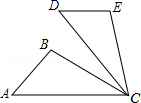
13.如图,△ACB≌△DCE,∠ACD=50°,则∠BCE的度数为_____.
14.若不等式组![]() 有且仅有3个整数解,则
有且仅有3个整数解,则![]() 的取值范围是___________.
的取值范围是___________.
15.顺次连接等腰梯形各边中点所得的四边形是_____.
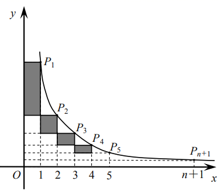
16.如图,在反比例函数![]() 的图像上有点
的图像上有点![]() 它们的横坐标依次为1,2,3,……,n,n+1,分别过点
它们的横坐标依次为1,2,3,……,n,n+1,分别过点![]() 作x轴,y轴的垂线,图中所构成的阴影部分面积从左到右依次为
作x轴,y轴的垂线,图中所构成的阴影部分面积从左到右依次为![]() ,则Sn=__________。(用含n的代数式表示)
,则Sn=__________。(用含n的代数式表示)
三、解下列各题(本大题共8小题,共72分)
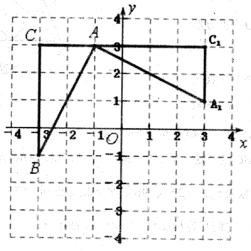
17.(8分)如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
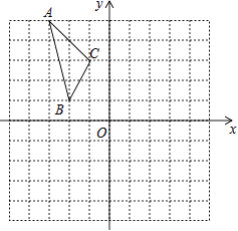
①若△ABC经过平移后得到△A1B1C1 , 已知点C1的坐标为(4,0),写出顶点A1 , B1的坐标;
②若△ABC和△A2B2C2关于原点O成中心对称图形,写出△A2B2C2的各顶点的坐标;
③将△ABC绕着点O按顺时针方向旋转90°得到△A3B3C3 , 写出△A3B3C3的各顶点的坐标.
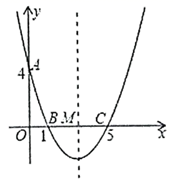
18.(8分)如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于
轴交于![]() 两点,其对称轴与
两点,其对称轴与![]() 轴交于点
轴交于点![]() .
.
(1)求抛物线的解析式和对称轴;
(2)在抛物线的对称轴上是否存在一点![]() ,使
,使![]() 的周长最小?若存在,请求出点
的周长最小?若存在,请求出点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(3)连接![]() ,在直线
,在直线![]() 的下方的抛物线上,是否存在一点
的下方的抛物线上,是否存在一点![]() ,使
,使![]() 的面积最大?若存在,请求出点
的面积最大?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
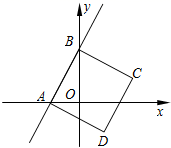
19.(8分)如图,一次函数y=2x+4的图象与x,y轴分别相交于点A,B,以AB为边作正方形ABCD(点D落在第四象限).
(1)求点A,B,D的坐标;
(2)联结OC,设正方形的边CD与x相交于点E,点M在x轴上,如果△ADE与△COM全等,求点M的坐标.
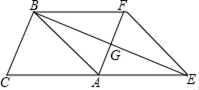
20.(8分)已知:如图,在△ABC中,AB=AC=4cm,将△ABC沿CA方向平移4cm得到△EFA,连接BE,BF;BE与AF交于点G
(1)判断BE与AF的位置关系,并说明理由;
(2)若∠BEC=15°,求四边形BCEF的面积.
21.(8分)已知关于x的一元二次方程x2﹣(n+3)x+3n=1.求证:此方程总有两个实数根.
22.(10分)如图,在平面直角坐标系中,有一![]() ,且
,且![]() ,
,![]() ,
,![]() ,已知
,已知![]() 是由
是由![]() 绕某点顺时针旋转得到的.
绕某点顺时针旋转得到的.
(1)请写出旋转中心的坐标是 ,旋转角是 度;
(2)以(1)中的旋转中心为中心,分别画出![]() 顺时针旋转90°、180°的三角形;
顺时针旋转90°、180°的三角形;
(3)设![]() 两直角边
两直角边![]() 、
、![]() 、斜边
、斜边![]() ,利用变换前后所形成的图案验证勾股定理.
,利用变换前后所形成的图案验证勾股定理.
23.(10分)本学期开学后,某校为了宣传关于新冠肺炎的防控知识,需印制若干份资料,印刷厂有甲、乙两种收费方式,甲种方式每份资料收费0.1元,另需收取制版费20元;乙种方式每份资料收费0.15元,不需要收取制版费.
(1)设资料印刷的费用为y元,印刷的数量为x份,请分别写出两种收费方式下y与x之间的函数关系式;
(2)该校某年级每次需印制100~600(含100和600)份资料,选择哪种印刷方式较合算?
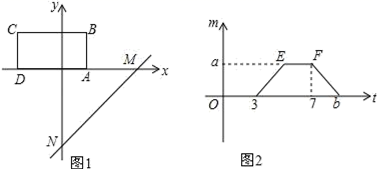
24.(12分)如图,将矩形ABCD置于平面直角坐标系中,其中AD边在x轴上,AB=2,直线MN:y=x﹣4沿x轴的负方向以每秒1个单位的长度平移,设在平移过程中该直线被矩形ABCD的边截得的线段长度为m,平移时间为t,m与t的函数图象如图2所示.
(1)点A的坐标为 ,矩形ABCD的面积为 ;
(2)求a,b的值;
(3)在平移过程中,求直线MN扫过矩形ABCD的面积S与t的函数关系式,并写出自变量t的取值范围.
参考答案
一、选择题(每小题3分,共30分)
1、B
2、A
3、C
4、C
5、B
6、A
7、C
8、C
9、C
10、D
二、填空题(本大题共有6小题,每小题3分,共18分)
11、1
12、6
13、50°
14、1≤a<2
15、菱形
16、![]()
三、解下列各题(本大题共8小题,共72分)
17、 (1)![]() (2,2),
(2,2),![]() (3,﹣2);(2)
(3,﹣2);(2)![]() (3,﹣5),
(3,﹣5),![]() (2,﹣1),
(2,﹣1),![]() (1,﹣3);(3)
(1,﹣3);(3)![]() (5,3),
(5,3),![]() (1,2),
(1,2),![]() (3,1).
(3,1).
18、(1)![]() ,抛物线的对称轴是
,抛物线的对称轴是![]() ;(2)
;(2)![]() 点坐标为
点坐标为![]() .理由见解析;(3)在直线
.理由见解析;(3)在直线![]() 的下方的抛物线上存在点
的下方的抛物线上存在点![]() ,使
,使![]() 面积最大.点
面积最大.点![]() 的坐标为
的坐标为![]() .
.
19、(1)A(-2,0),B(0,4),D(2,-2);(2)M(5,0).
20、(1)BE⊥AF,理由详见解析;(2)1.
21、见解析.
22、(1)旋转中心坐标是![]() ,旋转角是
,旋转角是![]() ;(2)见解析;(3)见解析
;(2)见解析;(3)见解析
23、(1)y1=0.1x+20;y2=0.15x;(2)当100≤x<400时,选择乙种方式较合算;当x=400时,甲、乙两种方式一样合算;当400<x≤600时,选择甲种方式较合算
24、(4)(4,7),3 ;(3)a=a=3![]() ,b=6;(3)S=
,b=6;(3)S=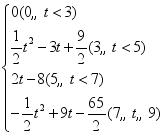 .
.
2023-2024学年安徽省合肥市北城片区九年级数学第一学期期末达标检测试题含答案: 这是一份2023-2024学年安徽省合肥市北城片区九年级数学第一学期期末达标检测试题含答案,共8页。试卷主要包含了若有意义,则x的取值范围是等内容,欢迎下载使用。
安徽省合肥市北城片区2023-2024学年数学八年级第一学期期末学业质量监测试题含答案: 这是一份安徽省合肥市北城片区2023-2024学年数学八年级第一学期期末学业质量监测试题含答案,共7页。试卷主要包含了下列各组中,没有公因式的一组是等内容,欢迎下载使用。
安徽省合肥市庐阳区2022-2023学年数学七下期末监测模拟试题含答案: 这是一份安徽省合肥市庐阳区2022-2023学年数学七下期末监测模拟试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁等内容,欢迎下载使用。












