哈尔滨松北区七校联考2022-2023学年七下数学期末调研试题含答案

哈尔滨松北区七校联考2022-2023学年七下数学期末调研试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项

1．考试结束后，请将本试卷和答题卡一并交回．

2．答题前，请务必将自己的姓名、准考证号用0．5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置．

3．请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符．

4．作答选择题，必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑；如需改动，请用橡皮擦干净后，再选涂其他答案．作答非选择题，必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答，在其他位置作答一律无效．

5．如需作图，须用2B铅笔绘、写清楚，线条、符号等须加黑、加粗．

一、选择题(每小题3分,共30分)

1．若式子有意义，则实数a的取值范围是（    ）

A．a＞﹣1 B．a＞﹣1且a≠2 C．a≥﹣1 D．a≥﹣1且a≠2

2．计算÷的结果是（   ）

A． B． C． D．

3．某班抽取6名同学参加体能测试，成绩如下:80，90，75，75，80，80.下列表述错误的是( )

A．众数是80 B．中位数是75 C．平均数是80 D．极差是15

4．如图，▱ABCD的周长为36，对角线AC、BD相交于点O，点E是CD的中点，BD=12，则△DOE的周长为（　　）

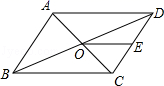
A．15 B．18 C．21 D．24

5．《国家宝藏》节目立足于中华文化宝库资源，通过对文物的梳理与总结，演绎文物背后的故事与历史，让更多的观众走进博物馆，让一个个馆藏文物鲜活起来．下面四幅图是我国一些博物馆的标志，其中是中心对称图形的是（    ）．

A． B． C． D．

6．若函数y=kx+b的图象如图所示，则关于x的不等式kx+b>0的解集为（   ）

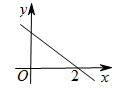
A．x＜2 B．x＞2 C．x≤2 D．x≥2

7．若＝，则的值是（）

A． B． C． D．

8．如图，亮亮书上的三角形被墨迹污染了一部分，他根据所学的知识很快就画了一个与书上完全一样的三角形，那么亮亮画图的依据是（  ）

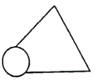
A． B． C． D．

9．10个人围成一圈做游戏.游戏的规则是：每个人心里都想一个数，并把目己想的数告诉与他相邻的两个人，然后每个人将与他相邻的两个人告诉他的数的平均数报出来，若报出来的数如图所示，则报出来的数是3的人心里想的数是（  ）

A．2 B． C．4 D．

10．已知四边形，有下列四组条件：①，；②，；③，；④，.其中不能判定四边形为平行四边形的一组条件是(    )

A．① B．② C．③ D．④

二、填空题(本大题共有6小题，每小题3分，共18分)

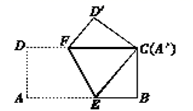
11．如图，将长8cm，宽4cm的矩形ABCD纸片折叠，使点A与C重合，则折痕EF的长为_________cm．

12．已知正n边形的每一个内角为150°，则n＝_____．

13．将50个数据分成5组，第1、2、3、4组的频数分别是2、8、10、15，则第5组的频率为_________

14．如图是一种“羊头”形图案，其作法是：从正方形①开始，以它的一边为斜边，向外作等腰直角三角形，然后再以其直角边为边，分别向外作正方形②和②′，…，依此类推，若正方形①的边长为64cm，则正方形⑦的边长为       cm．

15．一辆汽车，新车购买价20万元，第一年使用后折旧20%，以后该车的年折旧率有所变化，但它在第二，三年的年折旧率相同．已知在第三年年末，这辆车折旧后价值11.56万元，如果设这辆车第二、三年的年折旧率为x，那么根据题意，列出的方程为_____．

16．如图，正方形ABCD的边长为4，P为对角线AC上一点，且CP = 3，PE⊥PB交CD于点E，则PE =____________.

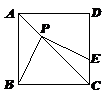
三、解下列各题(本大题共8小题，共72分)

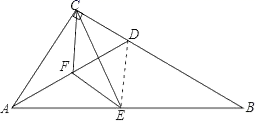
17．（8分）如图，Rt△ABC中，∠ACB＝90°，D是边BC上一点，点E、F分别是线段AB、AD中点，联结CE、CF、EF．

（1）求证：△CEF≌△AEF；

（2）联结DE，当BD＝2CD时，求证：AD＝2DE．

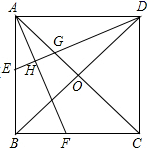
18．（8分）如图，正方形ABCD中，O是对角线的交点，AF平分BAC，DHAF于点H，交AC于G，DH延长线交AB于点E，求证：BE=2OG.

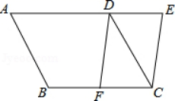
19．（8分）如图，将▱ABCD的AD边延长至点E，使DE＝AD，连接CE，F是BC边的中点，连接FD．

(1)求证：四边形CEDF是平行四边形；

(2)若AB＝3，AD＝4，∠A＝60°，求CE的长．

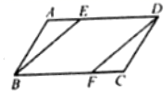
20．（8分）如图，在ABCD中，点E，F分别在AD，BC边上，且BE∥DF.

求证:(1)四边形BFDE是平行四边形；

 (2)AE=CF.

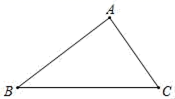
21．（8分）如图，在直角△ABC中，∠BAC＝90°，AB＝8，AC＝1．

（1）尺规作图：在BC上求作一点P，使点P到点A、B的距离相等；（保留作图痕迹，不写作法和证明）

（2）在（1）的条件下，连接AP，求△APC的周长．

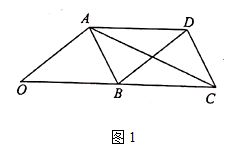
22．（10分）将沿直线平移到的位置，连接、.

（1）如图1，写出线段与的关系__________；

（2）如图1，求证：；

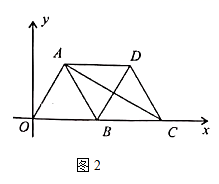
（3）如图2，当是边长为2的等边三角形时，以点为原点，所在的直线为轴建立平面直角坐标系.求出点的坐标，使得以、、、为顶点的四边形是平行四边形.

23．（10分）在所给的网格中，每个小正方形的网格边长都为1，按要求画出四边形，使它的四个顶点都在小正方形的顶点上．

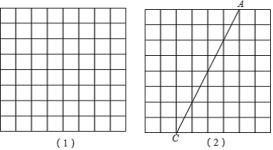
（1）在网格1中画出面积为20的菱形（非正方形）；

（2）在网格2中画出以线段为对角线、面积是24的矩形；直接写出矩形的周长         ．

24．（12分）甲、乙两家草莓采摘园的草莓品质相同，销售价格也相同．“五一期间”，两家均推出了优惠方案，甲采摘园的优惠方案是：游客进园需购买50元的门票，采摘的草莓六折优惠；乙采摘园的优惠方案是：游客进园不需购买门票，采摘园的草莓超过一定数量后，超过部分打折优惠．优惠期间，设某游客的草莓采摘量为x（千克），在甲采摘园所需总费用为（元），在乙采摘园所需总费用为（元），图中折线OAB表示与x之间的函数关系．

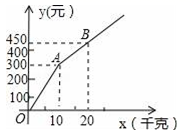
（1）甲、乙两采摘园优惠前的草莓销售价格是每千克       元；

（2）求、与x的函数表达式；

（3）在图中画出与x的函数图象，并写出选择甲采摘园所需总费用较少时，草莓采摘量x的范围．

参考答案

一、选择题(每小题3分,共30分)

1、D

2、C

3、B

4、A

5、A

6、A

7、A

8、C

9、B

10、D

二、填空题(本大题共有6小题，每小题3分，共18分)

11、

12、1

13、0.3

14、8

15、20（1﹣20%）（1﹣x）2＝11.1．

16、

三、解下列各题(本大题共8小题，共72分)

17、（1）见解析；（2）见解析.

18、证明见解析.

19、 (1)证明见解析；(2)CE＝.

20、（1）见解析；（2）见解析.

21、（1）见解析（2）11

22、（1）且；（2）见解析；（3），，

23、（1）见解析；（2）

24、（1）1；（2），；（3）＜x＜．