


2022-2023学年黑龙江省哈尔滨松北区七校联考七下数学期末教学质量检测模拟试题含答案
展开2022-2023学年黑龙江省哈尔滨松北区七校联考七下数学期末教学质量检测模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项
1.考生要认真填写考场号和座位序号。
2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。
3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。
一、选择题(每小题3分,共30分)
1.若二次根式![]() 有意义,则a的取值范围是( )
有意义,则a的取值范围是( )
A.a≥2 B.a≤2 C.a>2 D.a≠2
2.用配方法解一元二次方程![]() 时,下列变形正确的是( ).
时,下列变形正确的是( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.已知四边形 ABCD ,有以下四个条件:① AB ∥ CD ;② BC ∥ AD ;③ AB CD ;④ABC ADC .从这四个条件中任选两个,能使四边形 ABCD 成为平行四边形的选法有( )
A.3 种 B.4 种 C.5 种 D.6 种
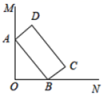
4.如图,![]() ,矩形
,矩形![]() 在
在![]() 的内部,顶点
的内部,顶点![]() ,
,![]() 分别在射线
分别在射线![]() ,
,![]() 上,
上,![]() ,
,![]() ,则点
,则点![]() 到点
到点![]() 的最大距离是( )
的最大距离是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.已知正比例函数![]() 的图象上两点
的图象上两点![]() 、
、![]() ,且
,且![]() ,下列说法正确的是
,下列说法正确的是![]()
![]()
A.![]() B.
B.![]() C.
C.![]() D.不能确定
D.不能确定
6.下列多项式中,分解因式不正确的是( )
A.a2+2ab=a(a+2b) B.a2-b2=(a+b)(a-b)
C.a2+b2=(a+b)2 D.4a2+4ab+b2=(2a+b)2
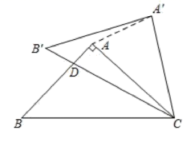
7.如图,![]() 中,
中,![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到出
得到出![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,连接
,连接![]() ,则
,则![]() 的度数为( )
的度数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.电影院里的座位按“×排×号”编排,小明的座位简记为(12,6),小菲的座位简记为(12,12),则小明与小菲坐的位置为( )
A.同一排 B.前后同一条直线上 C.中间隔六个人 D.前后隔六排
9.如图,以直角三角形的三边为边,分别向外作等边三角形、半圆、等腰直角三角形和正方形,上述四种情况的面积关系满足S1+S2=S3的图形有( )
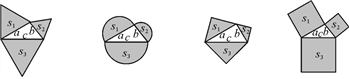
A.1个 B.2个 C.3个 D.4个
10.下列调查方式中适合的是( )
A.要了解一批节能灯的使用寿命,采用普查方式
B.调查你所在班级同学的身高,采用抽样调查方式
C.环保部门调查长江某段水域的水质情况,采用抽样调查方式
D.调查全市中学生每天的就寝时间,采用普查方式
二、填空题(本大题共有6小题,每小题3分,共18分)
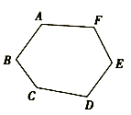
11.如图,![]() 是六边形
是六边形![]() 的一个内角.若
的一个内角.若![]() ,则
,则![]() 的度数为________.
的度数为________.
12.函数![]() 自变量的取值范围是______.
自变量的取值范围是______.
13.在我国古代数学著作《九章算术》中记载了一道有趣的数学问题:“今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适与岸齐.问水深、葭长备几何?”这个数学问题的意思是说:“有一个水池,水面是一个边长为![]() 丈(
丈(![]() 丈
丈![]() 尺)的正方形,在水池正中央长有一根芦苇,芦苇露出水面
尺)的正方形,在水池正中央长有一根芦苇,芦苇露出水面![]() 尺.如果把这根芦苇拉向岸边,它的顶端恰好到达岸边的水面.请问这个水池的深度和这根芦苇的长度各是多少?”设这个水池的深度是
尺.如果把这根芦苇拉向岸边,它的顶端恰好到达岸边的水面.请问这个水池的深度和这根芦苇的长度各是多少?”设这个水池的深度是![]() 尺,根据题意,可列方程为__________.
尺,根据题意,可列方程为__________.
14.将直线![]() 沿y轴向上平移5个单位长度后,所得图象对应的函数关系式为_________.
沿y轴向上平移5个单位长度后,所得图象对应的函数关系式为_________.
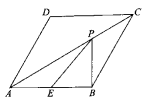
15.如图,在菱形ABCD中,∠ABC=120°,E是AB边的中点,P是AC边上一动点,PB+PE的最小值是![]() ,则AB的长为______.
,则AB的长为______.
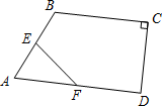
16.已知:如图,在四边形ABCD中,∠C=90°,E、F分别为AB、AD的中点,BC=6,CD=4,则EF=______.
三、解下列各题(本大题共8小题,共72分)
17.(8分)河南某校招聘干部一名 ,对![]() 、
、![]() 、
、![]() 三人进行素质测试,他们各项成绩如下表:将语言、综合知识、创新和处理问题能力按测试成绩
三人进行素质测试,他们各项成绩如下表:将语言、综合知识、创新和处理问题能力按测试成绩![]() 、
、![]() 、
、![]() 、
、![]() 比例计算,谁将被录用?
比例计算,谁将被录用?
测试项目 | 测试成绩 | ||
|
|
| |
语言 |
|
|
|
综合知识 |
|
|
|
创新 |
|
|
|
处理问题能力 |
|
|
|
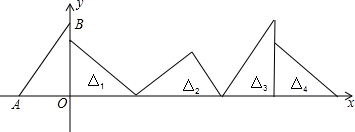
18.(8分)如图,在直角坐标系中,已知点A(﹣3,0),B(0,4),对△OAB连续作旋转变换,依次得到△1、△2、△3、△4…,则△2020的直角顶点的坐标为_____.
19.(8分)计算:
(1)![]()
(2)6![]() ÷
÷![]() +(1﹣
+(1﹣![]() )2
)2
20.(8分)因式分解
(1)![]()
(2)![]()
(3)![]()
(4)![]()
21.(8分)如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫格点,网格中有以格点A、B、C为顶点的△ABC,请你根据所学的知识回答下列问题:
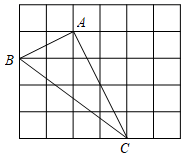
(1)求△ABC的面积;(2)判断△ABC的形状,并说明理由.
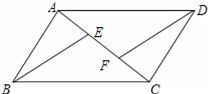
22.(10分)如图,E,F是平行四边形ABCD的对角线AC上的点,CE=AF.请你猜想:BE与DF有怎样的位置关系和数量关系?并对你的猜想加以证明.
23.(10分)解方程:
(1)![]() ;(2)
;(2)![]() .
.
24.(12分)某开发公司生产的960件新产品,需要精加工后,才能投放市场.现有甲、乙两个工厂都想加工这批产品,已知甲工厂单独加工完这批产品比乙工厂单独加工完这批产品多用20天,而乙工厂每天比甲工厂多加工8件产品,公司需付甲工厂加工费用每天80元,乙工厂加工费用每天120元.
(1)求甲、乙两个工厂每天各能加工多少件新产品.
(2)公司制定产品加工方案如下:可以由每个厂家单独完成;也可以由两个厂家同时合作完成.在加工过程中,公司需派一名工程师每天到厂进行技术指导,并负担每天5元的误餐补助费. 请你帮助公司选择一种既省时又省钱的加工方案,并说明理由.
参考答案
一、选择题(每小题3分,共30分)
1、A
2、D
3、B
4、B
5、A
6、C
7、C
8、A
9、D
10、C
二、填空题(本大题共有6小题,每小题3分,共18分)
11、![]()
12、![]()
13、![]()
14、![]()
15、1
16、![]()
三、解下列各题(本大题共8小题,共72分)
17、![]() 将被录用.
将被录用.
18、(8076,0)
19、(1)![]() +
+![]() ;(2)2
;(2)2![]() +1.
+1.
20、(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]()
21、(1)△ABC 的面积为5;(2)△ABC是直角三角形,见解析.
22、猜想:BE∥DF,BE=DF;证明见解析.
23、(2)原方程无解;(2)x= 2
24、 (1)甲、乙两个工厂每天各能加工16和24件.(2)合作.
2023-2024学年哈尔滨松北区七校联考九上数学期末监测模拟试题含答案: 这是一份2023-2024学年哈尔滨松北区七校联考九上数学期末监测模拟试题含答案,共8页。试卷主要包含了如图,已知∥∥,,那么的值是,抛物线y=,如果,那么等内容,欢迎下载使用。
2023-2024学年哈尔滨松北区七校联考数学八上期末复习检测模拟试题含答案: 这是一份2023-2024学年哈尔滨松北区七校联考数学八上期末复习检测模拟试题含答案,共7页。试卷主要包含了下列运算中错误的是,如图,能说明的公式是,不等式的解集是,-8的立方根是等内容,欢迎下载使用。
哈尔滨松北区七校联考2022-2023学年数学七下期末学业质量监测模拟试题含答案: 这是一份哈尔滨松北区七校联考2022-2023学年数学七下期末学业质量监测模拟试题含答案,共6页。试卷主要包含了考生必须保证答题卡的整洁,当x=1时,下列式子无意义的是,观察下列等式,对于一次函数,下列结论错误的是等内容,欢迎下载使用。












