


北京海淀人大附2022-2023学年七下数学期末综合测试模拟试题含答案
展开北京海淀人大附2022-2023学年七下数学期末综合测试模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
请考生注意:
1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。
2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.如图,P为平行四边形ABCD边AD上一点,E、F分别为PB、PC的中点,△PEF、△PDC、△PAB的面积分别为S、![]() 、
、![]() ,若S=2,则
,若S=2,则![]() +
+![]() =( ).
=( ).
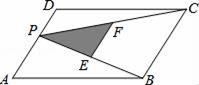
A.4 B.6 C.8 D.不能确定
2.下列说法:① 平方等于64的数是8;② 若a,b互为相反数,ab≠0,则![]() ;③ 若
;③ 若![]() ,则
,则![]() 的值为负数;④ 若ab≠0,则
的值为负数;④ 若ab≠0,则![]() 的取值在0,1,2,-2这四个数中,不可取的值是0.正确的个数为( )
的取值在0,1,2,-2这四个数中,不可取的值是0.正确的个数为( )
A.0个 B.1个 C.2个 D.3个
3.下列运算中正确的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.如图,丝带重叠的部分一定是( )

A.菱形 B.矩形 C.正方形 D.都有可能
5.若![]() 成立,则下列不等式成立的是( )
成立,则下列不等式成立的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
6.函数 y=![]() 中,自变量x的取值范围是( )
中,自变量x的取值范围是( )
A.x>﹣2 B.x≥﹣2 C.x≠2 D.x≤﹣2
7.若一个多边形每一个内角都是135º,则这个多边形的边数是 ( )
A.6 B.8 C.10 D.12
8.某班抽6名同学参加体能测试,成绩分别是1,90,75,75,1,1.则这组同学的测试成绩的中位数是( )
A.75 B.1 C.85 D.90
9.下列各曲线中哪个不能表示y是x的函数的是( )
A.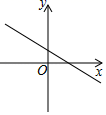 B.
B.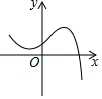 C.
C.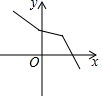 D.
D.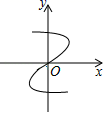
10.如图,平面直角坐标系中,在边长为1的正方形![]() 的边上有—动点
的边上有—动点![]() 沿正方形运动一周,
沿正方形运动一周,![]() 则
则![]() 的纵坐标
的纵坐标![]() 与点
与点![]() 走过的路程
走过的路程![]() 之间的函数关系用图象表示大致是( )
之间的函数关系用图象表示大致是( )
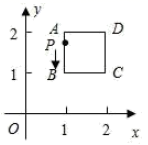
A. 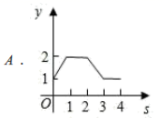 B.
B. 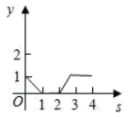 C.
C. 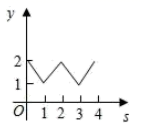 D.
D. 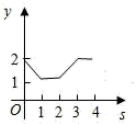
11.等式![]() •
•![]() =
=![]() 成立的条件是( )
成立的条件是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.如图,正方形OABC的兩辺OA、OC分別在x轴、y轴上,点D(5,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是( )
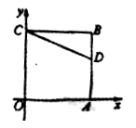
A.(1,10) B.(-2,0) C.(2,10)或(-2,0) D.(10,2)或(-2,0)
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13.如图,菱形ABCD的两条对角线相交于点O,若AC=6,BD=2,则菱形ABCD的周长是_____。
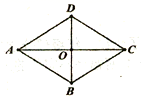
14.若三角形三边分别为6,8,10,那么它最长边上的中线长是_____.
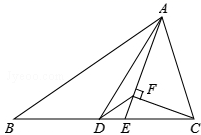
15.如图,△ABC中,AD是中线,AE是角平分线,CF⊥AE于F,AB=5,AC=2,则DF的长为_________.
16.分解因式:![]() ________.
________.
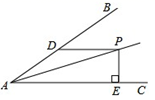
17.若∠BAC=30°,AP平分∠BAC,PD∥AC,且PD=6,PE⊥AC,则PE=________.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18.(5分)已知![]() 为原点,点
为原点,点![]() 及在第一象限的动点
及在第一象限的动点![]() ,且
,且![]() ,设
,设![]() 的面积为
的面积为![]() .
.
(1)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)求![]() 的取值范围;
的取值范围;
(3)当![]() 时,求
时,求![]() 点坐标;
点坐标;
(4)画出函数![]() 的图象.
的图象.
19.(5分)在平面直角坐标系中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() (k≠0)图象交于A、B两点,与y轴交于点C,与x轴交于点D,其中A点坐标为(﹣2,3).
(k≠0)图象交于A、B两点,与y轴交于点C,与x轴交于点D,其中A点坐标为(﹣2,3).
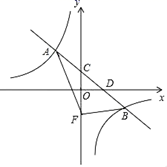
(1)求一次函数和反比例函数解析式.
(2)若将点C沿y轴向下平移4个单位长度至点F,连接AF、BF,求△ABF的面积.
(3)根据图象,直接写出不等式![]() 的解集.
的解集.
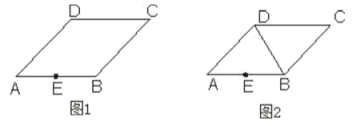
20.(8分)在菱形![]() 中,点
中,点![]() 是边
是边![]() 的中点,试分别在下列两个图形中按要求使用无刻度的直尺画图.
的中点,试分别在下列两个图形中按要求使用无刻度的直尺画图.
(1)在图1中,过点![]() 画
画![]() 的平行线;
的平行线;
(2)在图2中,连接![]() ,在
,在![]() 上找一点
上找一点![]() ,使点
,使点![]() 到点
到点![]() ,
,![]() 的距离之和最短.
的距离之和最短.
21.(10分)某商场计划从厂家购进甲、乙两种不同型号的电视机,已知进价分别为:甲种每台1500元,乙种每台2100元.
(1)若商场同时购进这两种不同型号的电视机50台,金额不超过76000元,商场有几种进货方案,并写出具体的进货方案.
(2)在(1)的条件下,若商场销售一台甲、乙型号的电视机的销售价分别为1650元、2300元,以上进货方案中,哪种进货方案获利最多?最多为多少元?
22.(10分)某校从初二(1)班和(2)班各选拔10名同学组成甲队和乙队,参加数学竞赛活动,此次竞赛共有10道选择题,答对8题(含8题)以上为优秀,两队选手答对题数统计如下:
答对题数 | 5 | 6 | 7 | 8 | 9 | 10 | 平均数( |
甲队选手 | 1 | 0 | 1 | 5 | 2 | 1 | 8 |
乙队选手 | 0 | 0 | 4 | 3 | 2 | 1 | a |
| 中位数 | 众数 | 方差(s2) | 优秀率 | |||
甲队选手 | 8 | 8 | 1.6 | 80% | |||
乙队选手 | b | c | 1.0 | m | |||
(1)上述表格中,a= ,b= ,c= ,m= .
(2)请根据平均数和众数的意义,对甲、乙两队选手进行评价.
23.(12分)为了提高学生书写汉字的能力,增强保护汉字的意识,某校举办了“汉子听写大赛”,学生经选拔后进入决赛,测试同时听写100个汉字,每正确听写出一个汉子得1分,本次决赛,学生成绩为x(分),且![]() (无满分),将其按分数段分为五组,绘制出以下不完整表格:
(无满分),将其按分数段分为五组,绘制出以下不完整表格:
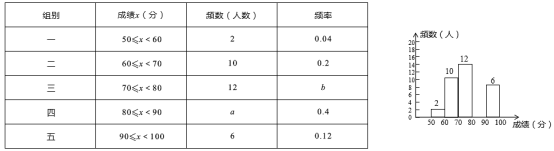
请根据表格提供的信息,解答以下问题:
(1)本次决赛共有________名学生参加;
(2)直接写出表中:a= ,b= 。
(3)请补全右面相应的频数分布直方图;
(4)若决赛成绩不低于80分为优秀,则本次大赛的优秀率为________.
参考答案
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、C
2、B
3、B
4、A
5、D
6、B
7、B
8、B
9、D
10、D
11、C
12、C
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13、![]()
14、1
15、![]()
16、 (a+1)(a-1)
17、1
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18、(1)S=−4x+48;(2)0<x<12;(3)P(1,3);(4)见解析.
19、(1)y=﹣![]() x+
x+![]() ,y=
,y=![]() ;(2)12;(3) x<﹣2或0<x<4.
;(2)12;(3) x<﹣2或0<x<4.
20、(1)详见解析;(2)详见解析.
21、(1)有2种进货方案:方案一:是购进甲种型号的电视机49台,乙种型号的电视机1台;方案二:是甲种型号的电视机1台,乙种型号的电视机0台;(2)方案一的利润大,最多为751元.
22、(1)8,8,7,![]() ;(2)见解析.
;(2)见解析.
23、(1)50;(2)20,0.24;(3)详见解析;(4)52%.
北京海淀人大附2023-2024学年数学八上期末学业质量监测试题含答案: 这是一份北京海淀人大附2023-2024学年数学八上期末学业质量监测试题含答案,共7页。试卷主要包含了答题时请按要求用笔,下列运算正确的是等内容,欢迎下载使用。
北京海淀人大附2023-2024学年数学八上期末检测模拟试题含答案: 这是一份北京海淀人大附2023-2024学年数学八上期末检测模拟试题含答案,共7页。试卷主要包含了9的平方根是,下列表情中,是轴对称图形的是,已知,则的值为等内容,欢迎下载使用。
北京市海淀区人大附中2022-2023学年数学七下期末达标测试试题含答案: 这是一份北京市海淀区人大附中2022-2023学年数学七下期末达标测试试题含答案,共7页。试卷主要包含了在下列命题中,是假命题的个数有等内容,欢迎下载使用。












