


内蒙古2021届高三上学期10月大联考试题 数学(理) Word版含答案
展开 www.ks5u.com数学(理科)试卷
www.ks5u.com数学(理科)试卷
(试卷总分:150分 考试时间:120分钟)
注意事项:
1.答题时,务必将自己的姓名、准考证号填写在答题卡规定的位置上。
2.答选择题时,必须使用2B铅笔将答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦擦干净后,再选涂其他答案标号。
3.答非选择题时,必须使用黑色墨水笔或黑色签字笔,将答案书写在答题卡规定的位置上。
4.所有题目必须在答题卡上作答,在试题卷上答题无效。
5.考试结束后,只将答题卡交回。
第I卷(选择题,共60分)
一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知全集U=R,A={x|x≤-1},B={x|x≥1},C={x|x≥0},则集合(![]() (A∪B))∩C=
(A∪B))∩C=
A.{x|x≥-1} B.{x|x≤1} C.{x|0≤x≤1} D.{x|0≤x<1}
2.已知i为虚数单位,复数z=![]() (a∈R)在复平面内对应点(x,y),则
(a∈R)在复平面内对应点(x,y),则
A.y=-2x+1 B.y=2x-1 C.y=-2x+5 D.y=3x-1
3.设向量a,b满足|a+b|=![]() ,|a-b|=
,|a-b|=![]() ,则a·b=
,则a·b=
A.1 B.2 C.3 D.5
4.函数y=(x3-x)2|x|的图象大致是

5.我国古代劳动人民在筑城筑堤、挖沟挖渠、建仓、建囤等工程中,积累了丰富的经验,总结出了一些有关体积、容积计算的方法,这些方法以实际问题的形式被收人我国古代数学名著《九章算术》中。《九章算术》将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,如图所示是一个阳马的三视图,则它的体积为
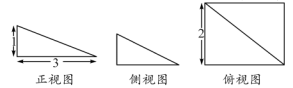
A.![]() B.1 C.2 D.3
B.1 C.2 D.3
6.在等比数列{an}中,a3=6,前三项和S3=18,则公比q的值为
A.1 B.-![]() C.1或-
C.1或-![]() D.-1或-
D.-1或-![]()
7.已知圆C1:x2+y2-kx-y=0和圆C2:x2+y2-2ky-1=0的公共弦所在的直线恒过定点M,且点M在直线mx+my=2上,则![]() 的最小值为
的最小值为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.已知sin2α=cosα,α≠![]() ,k∈Z,则cos2α=
,k∈Z,则cos2α=
A.![]() B.-
B.-![]() C.
C.![]() D.-
D.-![]()
9.对于不重合的两个平面α与β,给定下列条件:①存在平面γ,使得α,β都平行于γ;②存在平面γ,使得α,β都垂直于γ;③α内有不共线的三点到β的距离相等;④存在异面直线l,m,使得l//α,l//β,m//α,m//β。其中,可以判定α与β平行的条件有
A.1个 B.2个 C.3个 D.4个
10.已知抛物线C1:x2=4y,设C1的准线与y轴的交点为P,过点P作C1的切线,其中在第一象限内的切点为A。若双曲线C2:![]() 与抛物线C1相交于点A,且C1的焦点恰好是C2的一个焦点,则C2的离心率为
与抛物线C1相交于点A,且C1的焦点恰好是C2的一个焦点,则C2的离心率为
A.![]() B.
B.![]() C.
C.![]() -1 D.
-1 D.![]() +1
+1
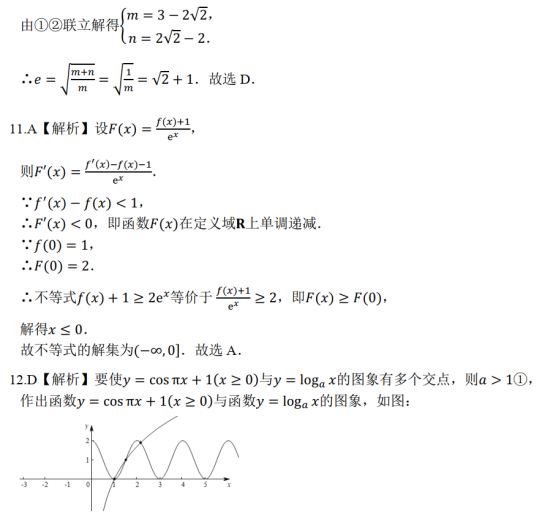
11.已知函数f(x)的定义域为R,f'(x)为f(x)的导函数。若f'(x)-f(x)<1,且f(0)=1,则不等式f(x)+1≥2ex的解集为
A.(-∞,0] B.[-1,+∞) C.[0,+∞) D.(-∞,-1]
12.若函数f(x)=cosπx+1与函数g(x)=logax(a>0且a≠1)的图象至少有五个交点,则实数a的取值范围是
A.(2,+∞) B.(1,2) C.(1,2] D.[2,+∞)
第II卷(非选择题,共90分)
二、填空题:本大题共4小题,每小题5分,共20分。把答案填在答题卡中的横线上。
13.五个人从左至右排成一行,最右端只能排甲或乙,最左端不能排甲,则不同的排法共有
种。
14.记D={(x,y)||x|+|y|=a,a>0},命题p:![]() (x,y)∈D,2x-y≥4,命题q:
(x,y)∈D,2x-y≥4,命题q:![]() (x,y)∈D,x2+y2≥1。若命题
(x,y)∈D,x2+y2≥1。若命题![]() p
p![]() q是真命题,则a的取值范围为 。
q是真命题,则a的取值范围为 。
15.设△ABC的三个内角A,B,C的对边分别为a,b,c,且cos(B-C)+cosA=![]() ,a2=bc,则角A的大小为 。
,a2=bc,则角A的大小为 。
16.正四棱柱ABCD-A1B1C1D1的外接球O的半径为2,当该正四棱柱的侧面积最大时,一个质点从A出发移动到C1,则沿正四棱柱表面移动的最短距离与直接穿过球O内部移动的最短距离的比值是 。
三、解答题:共70分,解答应写出文字说明、证明过程或演算步骤。第17~21题为必考题,每个试题考生都必须作答。第22、23题为选考题,考生根据要求作答。
(一)必考题:共60分。
17.(12分)设等差数列{an}的公差为d(d>1,n∈N*),前n项和为Sn,等比数列{bn}的公比为q。已知b1=a1,b2=4,3q=4d,S9=117。
(1)求数列{an},{bn}的通项公式;
(2)记cn=an·bn,求数列{cn}的前n项和Tn。
18.(12分)某县城为了打好蓝天保卫战,加快解决燃煤污染问题,全面实施散煤综合治理,而实施煤改电项目工程后,该县城近六个月的月用煤量逐渐减少,6月至11月的用煤量如下表所示:

(1)由于某些原因,用煤量y中一个数据丢失,但根据6至9月份的数据得出的样本平均值是3.5,求丢失的数据;
(2)请用(1)中得到的数据,根据6至9月份的数据,求出y关于x的线性回归方程![]() ;
;
(3)现在用(2)中得到的线性回归方程中得到的估计数据与10月、11月的实际数据的误差来判断该地区的改造项目是否达到预期,若误差均不超过0.3,则认为该地区的改造已经达到预期,否则认为改造未达预期,请判断该地区的煤改电项目是否达预期?
(参考公式:线性回归方程![]() ,其中
,其中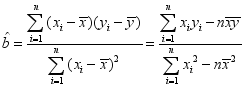 )
)
l9.(12分)如图,在三棱柱ABC-A1B1C1中,CC1⊥平面ABC,AC⊥BC,AC=BC=2,CC1=3,点D,E分别在棱AA1和棱CC1上,且AD=1,CE=2,点M为棱A1B1的中点。
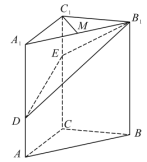
(1)求证:C1M⊥B1D;
(2)求二面角B-B1E-D的正弦值;
(3)求直线AB与平面DB1E所成角的正弦值。
20.(12分)已知函数f(x)=xcosx-sinx+![]() x2,f'(x)为f(x)的导函数。
x2,f'(x)为f(x)的导函数。
(1)若x∈[0,![]() ],f(x)≥ax2-sinx恒成立,求a的取值范围;
],f(x)≥ax2-sinx恒成立,求a的取值范围;
(2)证明:函数g(x)=f'(x)+2cosx在(0,![]() )上存在唯一零点。
)上存在唯一零点。
21.(12分)已知曲线C1:![]() 的短轴长为2
的短轴长为2![]() ,曲线C2:y2=4
,曲线C2:y2=4![]() x,C1的一个焦点在C2的准线上,
x,C1的一个焦点在C2的准线上,
(1)求曲线C1的方程;
(2)设曲线C1的左焦点为F1,右焦点为F2,若过点F1的直线l与曲线C1的y轴左侧部分(包含C1与y轴的交点)交于A,B两点,直线AF2与曲线C2交于C,D两点,直线BF2与曲线C2交于E,F两点,试求|CD|+|EF|的取值范围。
(二)选考题:共10分。请考生在第22、23题中选定一题作答,并用2B铅笔在答题卡上将所选题目对应的题号方框涂黑。按所涂题号进行评分,不涂、多涂均按所答第一题评分;多答按所答第一题评分。
22.(10分)已知直线l:![]() (t为参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C:ρ=2sinθ。
(t为参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C:ρ=2sinθ。
(1)求曲线C的直角坐标方程和直线l的直角坐标方程;
(2)求与直线l平行,且被曲线C截得的弦长为![]() 的直线l的方程。
的直线l的方程。
23.(10分)已知函数f(x)=|x+1|+|x-3|。
(1)求不等式f(x)<6的解集;
(2)若关于x的方程f(x)=|a-2|有解,求实数a的取值范围。












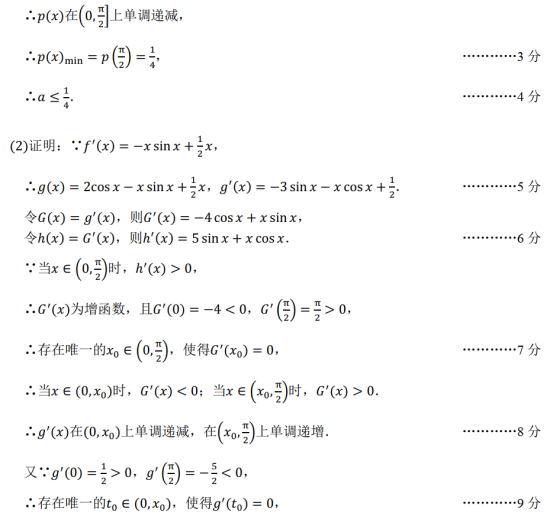


2024内蒙古部分名校高三上学期9月大联考试题数学(理)PDF版含解析: 这是一份2024内蒙古部分名校高三上学期9月大联考试题数学(理)PDF版含解析,共7页。
内蒙古2021届高三上学期10月大联考数学(理)试卷 PDF版含答案: 这是一份内蒙古2021届高三上学期10月大联考数学(理)试卷 PDF版含答案,共13页。
内蒙古2021届高三上学期10月大联考试题 数学(文) Word版含答案: 这是一份内蒙古2021届高三上学期10月大联考试题 数学(文) Word版含答案,共11页。试卷主要包含了考试结束后,只将答题卡交回,已知双曲线C等内容,欢迎下载使用。












