上海市徐汇区名校2022-2023学年数学七年级第二学期期末质量检测试题含答案

上海市徐汇区名校2022-2023学年数学七年级第二学期期末质量检测试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项：

1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。回答非选择题时，将答案写在答题卡上，写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交回。

一、选择题(每小题3分,共30分)

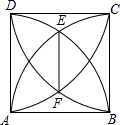
1．如图，已知正方形 ABCD 的边长为 1，以顶点 A、B 为圆心，1 为半径的两弧交于点 E， 以顶点 C、D 为圆心，1 为半径的两弧交于点 F，则 EF 的长为 （    ）

A． B． C． D．

2．函数的自变量的取值范围是（　　）

A．x≠3 B．x≥﹣2 C．x≥﹣2且x≠3 D．x≥3

3．若菱形的周长为16，高为2，则菱形两个邻角的比为（     ）

A．6:1 B．5:1 C．4:1 D．3:1

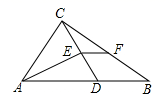
4．如图，在中，是上一点，，，垂足为，是的中点，若，则的长度为（    ）

A．36 B．18 C．9 D．5

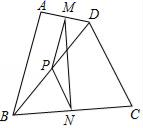
5．如图，在四边形ABCD中，已知AB＝CD，M、N、P分别是AD、BC、BD的中点∠ABD＝20°，∠BDC＝70°，则∠NMP的度数为（　　）

A．50° B．25° C．15° D．20

6．已知二次函数y=ax2+bx+c(a≠0)的图象如图所示，对称轴为x=﹣．下列结论中，正确的是(　　)

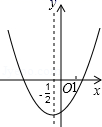
A．abc＞0 B．a+b=0 C．2b+c＞0 D．4a+c＜2b

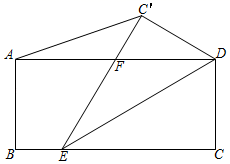
7．在矩形ABCD中，AB＝3，BC＝2，点E在BC边上，连接DE，将△DEC沿DE翻折，得到△DEC'，C'E交AD于点F，连接AC'．若点F为AD的中点，则AC′的长度为（　　）

A． B．2 C．2 D．+1

8．如图，在四边形中，与相交于点，,那么下列条件中不能判定四边形是菱形的为（   ）

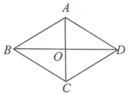
A．∠OAB=∠OBA B．∠OBA=∠OBC C．AD∥BC D．AD=BC

9．若分式的值为0，则x的值是（　　）

A．2 B．0 C．﹣2 D．任意实数

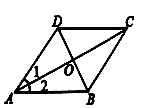
10．如图，中，对角线，相交于点，添加下列条件不能判定是菱形的是（    ）

A． B． C． D．

二、填空题(本大题共有6小题，每小题3分，共18分)

11．如图，点是的对称中心， ，是边上的点，且是边上的点，且，若分别表示和的面积则.

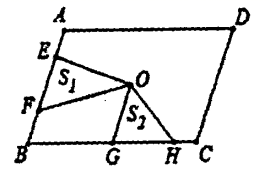
12．分解因式：4－m2＝_____．

13．在五边形中，若，则__________.

14．若关于x的分式方程﹣＝1无解，则m的值为_____．

15．根式+1的相反数是_____．

16．分式，，的最简的分母是_____.

三、解下列各题(本大题共8小题，共72分)

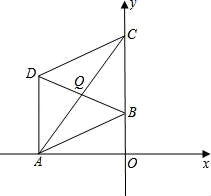
17．（8分）如图，在直角坐标系中，OA＝3，OC＝4，点B是y轴上一动点，以AC为对角线作平行四边形ABCD．

(1)求直线AC的函数解析式；

(2)设点B(0，m)，记平行四边形ABCD的面积为S，请写出S与m的函数关系式，并求当BD取得最小值时，函数S的值；

(3)当点B在y轴上运动，能否使得平行四边形ABCD是菱形？若能，求出点B的坐标；若不能，说明理由．

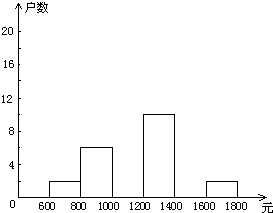
18．（8分）小龙在学校组织的社会调查活动中负责了解他所居住的小区450户居民的家庭收入情况、他从中随机调查了40户居民家庭收入情况（收入取整数，单位：元），并绘制了如下的频数分布表和频数分布直方图.

根据以上提供的信息，解答下列问题：
（1）补全频数分布表；
（2）补全频数分布直方图；
（3）请你估计该居民小区家庭属于中等收入（大于1000不足1600元）的大约有多少户？

19．（8分）解不等式组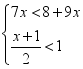：，并写出它的所有整数解．

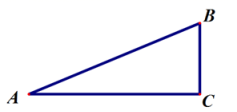
20．（8分）已知：如图，在中，，以点为圆心，的长为半径画弧，交线段于点，以点为圆心，长为半径画弧，交线段与点.

（1）根据题意用尺规作图补全图形（保留作图痕迹）；

（2）设

①线段的长度是方程的一个根吗？并说明理由.

②若线段，求的值.

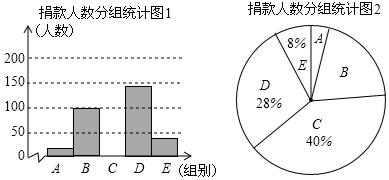
21．（8分）昆明市某校学生会干部对校学生会倡导的“牵手滇西”自愿捐款活动进行抽样调查，得到一组学生捐款情况的数据，对学校部分捐款人数进行调查和分组统计后，将数据整理成如图所示的统计图（图中信息不完整）．已知A、B两组捐款人数的比为1：1．

请结合以上信息解答下列问题．

（1）a＝　   　，本次调查样本的容量是　   　；

（2）先求出C组的人数，再补全“捐款人数分组统计图1”；

（3）根据统计情况，估计该校参加捐款的4100名学生有多少人捐款在20至40元之间．

22．（10分）某商场进行促销，购物满额即可获得次抽奖机会，抽奖袋中装有红色、黄色、白色三种除颜色外都相同的小球，从袋子中摸出个球，红色、黄色、白色分别代表一、二、三等奖．

(1)若小明获得次抽奖机会，小明中奖是　   　事件．(填随机、必然、不可能)

(2)小明观察一段时间后发现，平均每个人中会有人抽中一等奖，人抽中二等奖，若袋中共有个球，请你估算袋中白球的数量；

(3)在(2)的条件下，如果在抽奖袋中增加三个黄球，那么抽中一等奖的概率会怎样变化？请说明理由．

23．（10分）某商店准备进一批季节性小家电，单价40元．经市场预测，销售定价为52元时，可售出180个，定价每增加1元，销售量净减少10个；定价每减少1元，销售量净增加10个．因受库存的影响，每批次进货个数不得超过180个，商店若将准备获利2000元，则应进货多少个？定价为多少元？

24．（12分）因式分解：2

参考答案

一、选择题(每小题3分,共30分)

1、D

2、C

3、B

4、C

5、B

6、D

7、A

8、A

9、A

10、B

二、填空题(本大题共有6小题，每小题3分，共18分)

11、

12、（2＋m）（2−m）

13、130°

14、﹣2或1

15、

16、6x

三、解下列各题(本大题共8小题，共72分)

17、（1）；(2)  ①当m≤4时，S=－3m+12，②当m＞4时，S=3m－12（3）（0，）

18、（1）1200≤x＜1400，1400≤x＜1600；18人；5%；7.5%．（2）详见解析；（3）大约有338户．

19、解集为-4＜x＜2，不等式组的整数解是：﹣3，﹣2，﹣1、1．

20、（1）详见解析；（2）①线段的长度是方程的一个根，理由详见解析；②

21、 (1)20，100；（2）见解析；（3）3060人

22、 (1)必然；(2)9；(3)减小，理由见解析.

23、该商品每个定价为1元，进货100个.

24、2（a-b）2