


2022-2023学年辽宁省沈阳市第一六六中学数学七下期末教学质量检测试题含答案
展开2022-2023学年辽宁省沈阳市第一六六中学数学七下期末教学质量检测试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
考生须知:
1.全卷分选择题和非选择题两部分,全部在答题纸上作答。选择题必须用2B铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。
2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。
3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。
一、选择题(每小题3分,共30分)
1.如图,已知 BG 是∠ABC 的平分线,DE⊥AB 于点 E,DF⊥BC 于点 F,DE=6,则 DF 的长度是( )
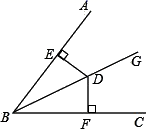
A.2 B.3 C.4 D.6
2.如图l1:y=x+3与l2:y=ax+b相交于点P(m,4),则关于x的不等式x+3≤ax+b的解为( )
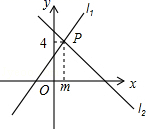
A.x≥4 B.x<m C.x≥m D.x≤1
3.在平面直角坐标系xOy中,线段AB的两个端点坐标分别为A(-1,-1),B(1,2),平移线段AB得到线段A’B’(点A与A’对应),已知A’的坐标为(3,-1),则点B’的坐标为( )
A.(4,2) B.(5,2) C.(6,2) D.(5,3)
4.已知等腰三角形的周长是10,底边长y是腰长x的函数,则下列图象中,能正确反映y与x之间函数关系的图象是( )
A. B.
B.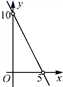 C.
C.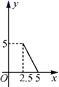 D
D
5.我校是教育部的全国青少年校园足球“满天星”训练基地,旨在“踢出快乐,拼出精彩”,如图,校园足球图片正中的黑色正五边形的内角和是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.将含有30°角的直角三角板OAB如图放置在平面直角坐标系中,OB在x轴上,若OA=2,将三角板绕原点O顺时针旋转75°,则点A的对应点A′的坐标为( )
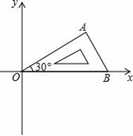
A.(![]() ,﹣1) B.(1,﹣
,﹣1) B.(1,﹣![]() ) C.(
) C.(![]() ,﹣
,﹣![]() ) D.(﹣
) D.(﹣![]() ,
,![]() )
)
7.张华在一次数学活动中,利用“在面积一定的矩形中,正方形的周长最短”的结论,推导出“式子![]() (x>0)的最小值是1”.其推导方法如下:在面积是1的矩形中设矩形的一边长为x,则另一边长是
(x>0)的最小值是1”.其推导方法如下:在面积是1的矩形中设矩形的一边长为x,则另一边长是![]() ,矩形的周长是1(
,矩形的周长是1(![]() );当矩形成为正方形时,就有x=
);当矩形成为正方形时,就有x=![]() (x>0),解得x=1,这时矩形的周长1(
(x>0),解得x=1,这时矩形的周长1(![]() )=4最小,因此
)=4最小,因此![]() (x>0)的最小值是1.模仿张华的推导,你求得式子
(x>0)的最小值是1.模仿张华的推导,你求得式子![]() (x>0)的最小值是( )
(x>0)的最小值是( )
A.1 B.1 C.6 D.10
8.下列函数中,自变量x的取值范围是x≥3的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.课堂上老师在黑板上布置了右框所示的题目,小聪马上发现了其中有一道题目错了,你知道是哪道题目吗?( )
用平方差公式分解下列各式:
(1)![]()
(2)![]()
(3)![]()
(4)![]()
A.第1道题 B.第2道题 C.第3道题 D.第4道题
10.如图,点A1、B1、C1分别为△ABC的边BC、CA、AB的中点,点A2、B2、C2分别为△A1B1C1的边B1C1、C1A1、A1B1的中点,若△ABC的面积为1,则△A2B2C2的面积为( )
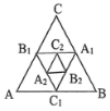
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(本大题共有6小题,每小题3分,共18分)
11.在△ABC中,AB=10,CA=8,BC=6,∠BAC的平分线与∠BCA的平分线交于点I,且DI∥BC交AB于点D,则DI的长为____.
12.如图,矩形![]() 的顶点
的顶点![]() 分别在反比例函数
分别在反比例函数![]() 的图像上,顶点
的图像上,顶点![]() 在
在![]() 轴上,则矩形
轴上,则矩形![]() 的面积是______.
的面积是______.

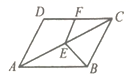
13.如图,平行四边形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是对角线
是对角线![]() 上一动点,点
上一动点,点![]() 是边
是边![]() 上一动点,连接
上一动点,连接![]() 、
、![]() ,则
,则![]() 的最小值是______.
的最小值是______.
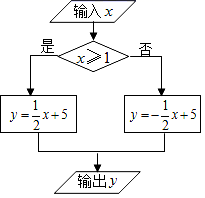
14.根据图中的程序,当输入数值﹣2时,输出数值为a;若在该程序中继续输入数值a时,输出数值为_____.
15.二次函数![]() 的图象的顶点是__________.
的图象的顶点是__________.
16.若关于x的一元二次方程![]() x2﹣2kx+1-4k=0有两个相等的实数根,则代数式(k-2)2+2k(1-k)的值为______.
x2﹣2kx+1-4k=0有两个相等的实数根,则代数式(k-2)2+2k(1-k)的值为______.
三、解下列各题(本大题共8小题,共72分)
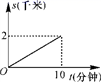
17.(8分)甲乙两车分别从A.B两地相向而行,甲车出发1小时后乙车出发,并以各自速度匀速行驶,两车相遇后依然按照原速度原方向各自行驶,如图所示是甲乙两车之间的距离S(千米)与甲车出发时间t(小时)之间的函数图象,其中D点表示甲车到达B地,停止行驶。
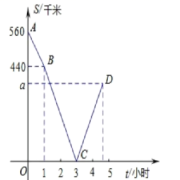
(1)A、B两地的距离___千米;乙车速度是___;a=___.
(2)乙出发多长时间后两车相距330千米?
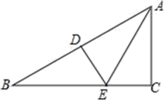
18.(8分)如图,在△ABC中,∠B=30°,边AB的垂直平分线分别交AB和BC于点D,E,且AE平分∠BAC.
(1)求∠C的度数;
(2)若CE=1,求AB的长.
19.(8分)光华农机租赁公司共有50台联合收割机,其中甲型20台,乙型30台,先将这50台联合收割机派往A、B两地区收割小麦,其中30台派往A地区,20台派往B地区.两地区与该农机租赁公司商定的每天的租赁价格见表:
| 每台甲型收割机的租金 | 每台乙型收割机的租金 |
A地区 | 1800 | 1600 |
B地区 | 1600 | 1200 |
(1)设派往A地区x台乙型联合收割机,租赁公司这50台联合收割机一天获得的租金为y(元),求y与x间的函数关系式,并写出x的取值范围;
(2)若使农机租赁公司这50台联合收割机一天获得的租金总额不低于79 600元,说明有多少种分配方案,并将各种方案设计出来;
(3)如果要使这50台联合收割机每天获得的租金最高,请你为光华农机租赁公司提一条合理化建议.
20.(8分)在2019年春季环境整治活动中,某社区计划对面积为![]() 的区域进行绿化.经投标,由甲、乙两个工程队来完成,若甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,并且在独立完成面积为
的区域进行绿化.经投标,由甲、乙两个工程队来完成,若甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,并且在独立完成面积为![]() 区域的绿化时,甲队比乙队少用5天.
区域的绿化时,甲队比乙队少用5天.
(1)求甲、乙两工程队每天能完成绿化的面积;
(2)设甲工程队施工![]() 天,乙工程队施工
天,乙工程队施工![]() 天,刚好完成绿化任务,求
天,刚好完成绿化任务,求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)在(2)的条件下,若甲队每天绿化费用是0.6万元,乙队每天绿化费用为0.25万元,且甲乙两队施工的总天数不超过25天,则如何安排甲乙两队施工的天数,使施工总费用最低?并求出最低费用.
21.(8分)课堂上老师讲解了比较![]() 和
和![]() 的方法,观察发现11-10=15-14=1,于是比较这两个数的倒数:
的方法,观察发现11-10=15-14=1,于是比较这两个数的倒数:
 ,
,
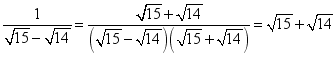 ,
,
因为![]() >
>![]() ,所以
,所以![]() >
>![]() ,则有
,则有![]() <
<![]() .
.
请你设计一种方法比较![]() 与
与![]() 的大小.
的大小.
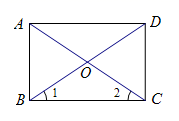
22.(10分)如图,四边形ABCD是平行四边形,对角线AC,BD相交于点O,且∠1=∠1.求证:四边形ABCD是矩形.
23.(10分)某经销商从市场得知如下信息:
| A品牌计算器 | B品牌计算器 |
进价(元/台) | 700 | 100 |
售价(元/台) | 900 | 160 |
他计划一次性购进这两种品牌计算器共100台(其中A品牌计算器不能超过50台),设该经销商购进A品牌计算器x台(x为整数),这两种品牌计算器全部销售完后获得利润为y元.
(1)求y与x之间的函数关系式;
(2)若要求A品牌计算器不得少于48台,求该经销商有哪几种进货方案?
(3)选择哪种进货方案,该经销商可获利最大?最大利润是多少元?
24.(12分)如图,将一矩形纸片OABC放在平面直角坐标系中,![]() ,
,![]() ,
,![]() .动点Q从点O出发以每秒1个单位长的速度沿OC向终点C运动,运动
.动点Q从点O出发以每秒1个单位长的速度沿OC向终点C运动,运动![]() 秒时,动点P从点A出发以相同的速度沿AO向终点O运动.当其中一点到达终点时,另一点也停止运动.设点P的运动时间为t(秒).
秒时,动点P从点A出发以相同的速度沿AO向终点O运动.当其中一点到达终点时,另一点也停止运动.设点P的运动时间为t(秒).
(1)OP =____________, OQ =____________;(用含t的代数式表示)
(2)当![]() 时,将△OPQ沿PQ翻折,点O恰好落在CB边上的点D处.
时,将△OPQ沿PQ翻折,点O恰好落在CB边上的点D处.
①求点D的坐标;
②如果直线y = kx + b与直线AD平行,那么当直线y = kx + b与四边形PABD有交点时,求b 的取值范围.
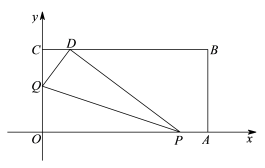
参考答案
一、选择题(每小题3分,共30分)
1、D
2、D
3、B
4、D
5、C
6、C
7、C
8、D
9、C
10、D
二、填空题(本大题共有6小题,每小题3分,共18分)
11、2.5
12、3
13、![]()
14、8 .
15、![]()
16、![]()
三、解下列各题(本大题共8小题,共72分)
17、(1)560千米;100;![]() ;(2)乙出发0.5小时或3.5小时后两车相距330千米.
;(2)乙出发0.5小时或3.5小时后两车相距330千米.
18、(1)![]() ;(2)
;(2)![]() .
.
19、(1)y=200x+74000(10≤x≤30)
(2)有三种分配方案,
方案一:派往A地区的甲型联合收割机2台,乙型联合收割机28台,其余的全派往B地区;
方案二:派往A地区的甲型联合收割机1台,乙型联合收割机29台,其余的全派往B地区;
方案三:派往A地区的甲型联合收割机0台,乙型联合收割机30台,其余的全派往B地区;
(3)派往A地区30台乙型联合收割机,20台甲型联合收割机全部派往B地区,使该公司50台收割机每天获得租金最高.
20、(1)甲、乙两工程队每天能完成绿化面积分别为![]() 和
和![]() ;(2)
;(2)![]() ;(3)甲工程队施工15天,乙工程队施工10天,则施工总费用最低,最低费用为11.5万.
;(3)甲工程队施工15天,乙工程队施工10天,则施工总费用最低,最低费用为11.5万.
21、方法见解析.
22、参见解析.
23、 (1)y=140x+1;(2)三种方案,见解析;(3)选择A50台、B50台的进货方案,经销商可获利最大,最大利润是13000元.
24、(1)6-t; t+![]() (2)①D(1,3) ②3≤b≤
(2)①D(1,3) ②3≤b≤![]()
2023-2024学年辽宁省沈阳市第一六六中学数学九上期末检测试题含答案: 这是一份2023-2024学年辽宁省沈阳市第一六六中学数学九上期末检测试题含答案,共8页。试卷主要包含了答题时请按要求用笔,下图中几何体的左视图是,如图等内容,欢迎下载使用。
2023-2024学年辽宁省沈阳市第一六六中学数学八年级第一学期期末达标检测试题含答案: 这是一份2023-2024学年辽宁省沈阳市第一六六中学数学八年级第一学期期末达标检测试题含答案,共6页。
2022-2023学年辽宁省沈阳市一三四中学数学七下期末经典试题含答案: 这是一份2022-2023学年辽宁省沈阳市一三四中学数学七下期末经典试题含答案,共7页。试卷主要包含了已知,使有意义的取值范围是,过原点和点的直线的解析式为等内容,欢迎下载使用。













