


2022-2023学年辽宁省大连市新民间联盟七下数学期末达标检测试题含答案
展开这是一份2022-2023学年辽宁省大连市新民间联盟七下数学期末达标检测试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁等内容,欢迎下载使用。
2022-2023学年辽宁省大连市新民间联盟七下数学期末达标检测试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
考生请注意:
1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。
2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。
3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.如图,一次函数![]() 的图象交
的图象交![]() 轴于点
轴于点![]() ,则不等式
,则不等式![]() 的解集为( )
的解集为( )
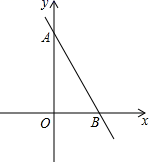
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.已知一元二次方程x2-2x-1=0的两根分别为x1,x2,则![]() 的值为( )
的值为( )
A.2 B.-1
C.-![]() D.-2
D.-2
3.下列函数中是一次函数的是![]()
![]()
A.![]() B.
B.![]()
C.![]() D.
D.![]()
4.利用反证法证明命题“在![]() 中,若
中,若![]() ,则
,则![]() ”时,应假设
”时,应假设![]()
![]()
A.若![]() ,则
,则![]() B.若
B.若![]() ,则
,则![]()
C.若![]() ,则
,则![]() D.若
D.若![]() ,则
,则![]()
5.下列函数中,对于任意实数x1,x2,当x1>x2时,满足y1<y2的是( )
A.y=﹣3x+2 B.y=2x+1 C.y=5x D.y=![]()
6.已知函数y1=![]() 和y2=ax+5的图象相交于A(1,n),B(n,1)两点.当y1>y2时,x的取值范围是( )
和y2=ax+5的图象相交于A(1,n),B(n,1)两点.当y1>y2时,x的取值范围是( )
A.x≠1 B.0<x<1 C.1<x<4 D.0<x<1或x>4
7. “龟兔首次赛跑”之后,输了比赛的兔子总结惨痛教训后.决定和乌龟再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(![]() 表示乌龟从起点出发所行的时间,
表示乌龟从起点出发所行的时间,![]() 表示乌龟所行的路程,
表示乌龟所行的路程,![]() 表示兔子所行的路程.下列说法中:①“龟兔再次赛跑”的路程为1000米;②兔子和乌龟同时从起点出发;③乌龟在途中休息了10分钟;④兔子在途中750米处上了乌龟.正确的有:( )
表示兔子所行的路程.下列说法中:①“龟兔再次赛跑”的路程为1000米;②兔子和乌龟同时从起点出发;③乌龟在途中休息了10分钟;④兔子在途中750米处上了乌龟.正确的有:( )
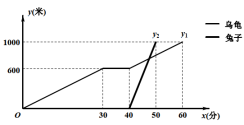
A.1个 B.2个 C.3个 D.4个
8.小苏和小林在如图①所示的跑道上进行![]() 米折返跑.在整个过程中,跑步者距起跑线的距离
米折返跑.在整个过程中,跑步者距起跑线的距离![]() (单位:
(单位:![]() )与跑步时间
)与跑步时间![]() (单位:
(单位:![]() )的对应关系如图②所示.下列叙述正确的是( ).
)的对应关系如图②所示.下列叙述正确的是( ).
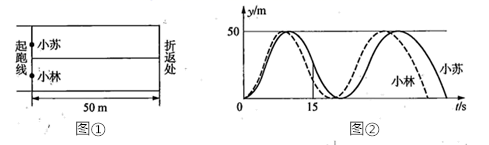
A.两人从起跑线同时出发,同时到达终点
B.小苏跑全程的平均速度大于小林跑全程的平均速度
C.小苏前![]() 跑过的路程大于小林前
跑过的路程大于小林前![]() 跑过的路程
跑过的路程
D.小林在跑最后![]() 的过程中,与小苏相遇2次
的过程中,与小苏相遇2次
9.我校是教育部的全国青少年校园足球“满天星”训练基地,旨在“踢出快乐,拼出精彩”,如图,校园足球图片正中的黑色正五边形的内角和是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.若关于![]() 的一元二次方程
的一元二次方程![]() 通过配方法可以化成
通过配方法可以化成![]() 的形式,则
的形式,则![]() 的值不可能是
的值不可能是![]()
![]()
A.3 B.6 C.9 D.10
11.如图,若要用“![]() ”证明
”证明![]() ,则还需补充的条件是( )
,则还需补充的条件是( )
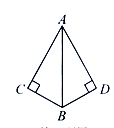
A.![]() B.
B.![]() 或
或![]()
C.![]() 且
且![]() D.
D.![]()
12.下图是北京世界园艺博览会园内部分场馆的分布示意图,在图中,分别以正东、正北方向为![]() 轴、
轴、![]() 轴的正方向建立平向直角坐标系,如果表示演艺中心的点的坐标为
轴的正方向建立平向直角坐标系,如果表示演艺中心的点的坐标为![]() ,表示水宁阁的点的坐标为
,表示水宁阁的点的坐标为![]() ,那么下列各场馆的坐标表示正确的是( )
,那么下列各场馆的坐标表示正确的是( )
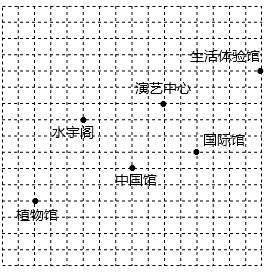
A.中国馆的坐标为![]()
B.国际馆的坐标为![]()
C.生活体验馆的坐标为![]()
D.植物馆的坐标为![]()
二、填空题(每题4分,满分20分,将答案填在答题纸上)
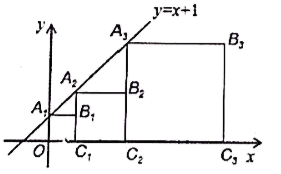
13.正方形![]() ,
,![]() ,
,![]() ,...按如图的方式放置,点
,...按如图的方式放置,点![]() ,
,![]() ,
,![]() ...和点
...和点![]() ,
,![]() ,
,![]() ...分别在直线
...分别在直线![]() 和
和![]() 轴上,则点
轴上,则点![]() 的坐标为_______.
的坐标为_______.
14.已知正多边形的一个外角等于40°,那么这个正多边形的边数为__________.
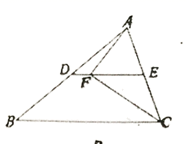
15.如图,![]() 为
为![]() 的中位线,点
的中位线,点![]() 在
在![]() 上,且
上,且![]() 为直角,若
为直角,若![]() ,
,![]() ,则
,则![]() 的长为__________
的长为__________![]() .
.
16.对于代数式m,n,定义运算“※”:m※n=![]() (mn≠0),例如:4※2=
(mn≠0),例如:4※2=![]() .若(x﹣1)※(x+2)=
.若(x﹣1)※(x+2)=![]() ,则2A﹣B=_____.
,则2A﹣B=_____.
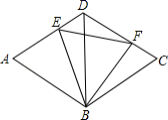
17.如图,菱形![]() 的边长为2,点
的边长为2,点![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 上的两个动点,且满足
上的两个动点,且满足![]() ,设
,设![]() 的面积为
的面积为![]() ,则
,则![]() 的取值范围是__.
的取值范围是__.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18.(5分)某学校要从甲乙两名射击运动员中挑选一人参加全市比赛,在选拔赛中,每人进行了5次射击,甲的成绩(环)为:9.7,10,9.6,9.8,9.9;乙的成绩的平均数为9.8,方差为0.032;
(1)甲的射击成绩的平均数和方差分别是多少?
(2)据估计,如果成绩的平均数达到9.8环就可能夺得金牌,为了夺得金牌,应选谁参加比赛?
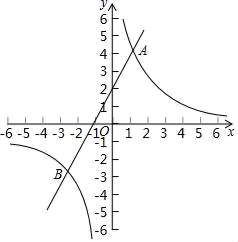
19.(5分)如图直线y=2x+m与y=![]() (n≠0)交于A,B两点,且点A的坐标为(1,4).
(n≠0)交于A,B两点,且点A的坐标为(1,4).
(1)求此直线和双曲线的表达式;
(2)过x轴上一点M作平行于y轴的直线1,分别与直线y=2x+m和双曲线y=![]() (n≠0)交于点P,Q,如果PQ=2QM,求点M的坐标.
(n≠0)交于点P,Q,如果PQ=2QM,求点M的坐标.
20.(8分)已知矩形![]() ,
,![]() 为
为![]() 边上一点,
边上一点,![]() ,点
,点![]() 从
从![]() 点出发,以每秒
点出发,以每秒![]() 个单位的速度沿着
个单位的速度沿着![]() 边向终点
边向终点![]() 运动,连接
运动,连接![]() ,设点
,设点![]() 运动的时间为
运动的时间为![]() 秒,则当
秒,则当![]() 的值为__________时,
的值为__________时,![]() 是以
是以![]() 为腰的等腰三角形.
为腰的等腰三角形.
21.(10分)计算
(1)(![]() )-(
)-(![]() )
)
(2)(2![]() +3)(2
+3)(2![]() -3)
-3)
22.(10分)为保护环境,我市公交公司计划购买A型和B型两种环保节能公交车共10辆.若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元.
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在某线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客总和不少于680万人次,则该公司有哪几种购车方案?
(3)在(2)的条件下,哪种购车方案总费用最少?最少总费用是多少万元?
23.(12分)百货商店销售某种冰箱,每台进价2500元.市场调研表明:当销售价为2900元时,平均每天能售出8台;每台售价每降低10元时,平均每天能多售出1台.(销售利润=销售价-进价)
(1)如果设每台冰箱降价x元,那么每台冰箱的销售利润为______元,平均每天可销售冰箱______台;(用含x的代数式表示)
(2)商店想要使这种冰箱的销售利润平均每天达到5600元,且尽可能地清空冰箱库存,每台冰箱的定价应为多少元?
参考答案
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、C
2、D
3、D
4、C
5、A
6、D
7、C
8、D
9、C
10、D
11、B
12、A
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13、![]()
14、1
15、1
16、-1
17、![]() .
.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18、(1)9.8,0.02;(2)应选甲参加比赛.
19、 (1)直线的解析式为y=2x+2,反比例函数的解析式为y=![]() ;(2)M(﹣3,0)或(2,0).
;(2)M(﹣3,0)或(2,0).
20、![]() 或
或![]()
21、 (1) ![]() ;(2)-1.
;(2)-1.
22、(1)购买A型公交车每辆需100万元,购买B型公交车每辆需15![]() 0万元.
0万元.
(2)三种方案:①购买A型公交车6辆,则B型公交车4辆;②购买A型公交车7辆,则B型公交车3辆;③购买A型公交车8辆,则B型公交车2辆;
(3)购买A型公交车8辆,B型公交车2辆费用最少,最少费用为1100万元.
23、(1)![]() ,
,![]() ;(2) 应定价2700元.
;(2) 应定价2700元.
相关试卷
这是一份辽宁省大连市新民间联盟2023-2024学年数学九上期末经典试题含答案,共8页。试卷主要包含了在比例尺为1等内容,欢迎下载使用。
这是一份2023-2024学年辽宁省大连市新民间联盟八上数学期末监测试题含答案,共7页。试卷主要包含了在平面直角坐标系中,点P,如果,那么的值为等内容,欢迎下载使用。
这是一份2023-2024学年辽宁省大连市新民间联盟八上数学期末联考试题含答案,共6页。试卷主要包含了考生必须保证答题卡的整洁,下面计算正确的是,下列各式等内容,欢迎下载使用。








