


2022-2023学年肇庆市重点中学数学七年级第二学期期末监测模拟试题含答案
展开2022-2023学年肇庆市重点中学数学七年级第二学期期末监测模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.答题时请按要求用笔。
3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折暴、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.某校八年级(3)班体训队员的身高(单位:cm)如下:169,165,166,164,169,167,166,169,166,165,获得这组数据方法是( )
A.直接观察 B.查阅文献资料 C.互联网查询 D.测量
2.分式![]() 有意义的条件是( )
有意义的条件是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.下表是某校![]() 名男子足球队的年龄分布:
名男子足球队的年龄分布:
年龄(岁) |
|
|
|
|
频数 |
|
|
|
|
该校男子足球队队员的平均年龄为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.将方程x2+4x+1=0配方后,原方程变形为( )
A.(x+2)2=3 B.(x+4)2=3 C.(x+2)2=﹣3 D.(x+2)2=﹣5
5.如果一次函数y=kx+b(k、b是常数,k≠0)的图象经过第一、二、四象限,那么k、b应满足的条件是( )
A.k>0,且b>0 B.k<0,且b>0 C.k>0,且b<0 D.k<0,且b<0
6.如图,正方形ABCD的边长为4,P为正方形边上一动点,运动路线
是A→D→C→B→A,设P点经过的路程为x,以点A、P、D为顶点的三
角形的面积是y.则下列图象能大致反映y与x的函数关系的是( )
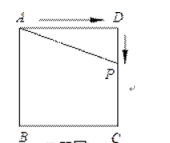
A. B.
B.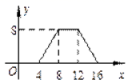 C.
C.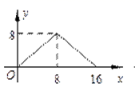 D.
D.
7.直线y=2x向下平移2个单位长度得到的直线是( )
A.y=2(x+2) B.y=2(x﹣2) C.y=2x﹣2 D.y=2x+2
8.如图,![]() 沿直线边BC所在的直线向右平移得到
沿直线边BC所在的直线向右平移得到![]() ,下列结论中不一定正确的是
,下列结论中不一定正确的是![]()
![]()

A.![]() B.
B.![]()
C.![]() D.
D.![]()
9.已知A(x1,y1),B(x2,y2)是一次函数y=(2a﹣1)x﹣3图象上的两点,当x1<x2时,有y1>y2,则a的取值范围是( )
A.a<2 B.a>![]() C.a>2 D.a<
C.a>2 D.a<![]()
10.为打击毒品犯罪,我县缉毒警察乘警车,对同时从县城乘汽车出发到A地的两名毒犯实行抓捕,警车比汽车提前15分钟到A地,A地距离县城8千米,警车的平均速度是汽车平均速度的2.5倍,若设汽车的平均速度是每小时x千米,根据题意可列方程为( )
A.![]() +15=
+15=![]() B.
B.![]() =
=![]() +15
+15
C.![]() =
=![]() D.
D.![]() =
=![]()
![]()
11.如图,直线![]() 经过点A(a,
经过点A(a,![]() )和点B(
)和点B(![]() ,0),直线
,0),直线![]() 经过点A,则当
经过点A,则当![]() 时,x的取值范围是( )
时,x的取值范围是( )

A.x>-1 B.x<-1 C.x>-2 D.x<-2
12.若样本x1+1,x2+1,…,xn+1的平均数为10,方差为2,则对于样本x1+2,x2+2,…,xn+2,下列结论正确的是( )
A.平均数为10,方差为2 B.平均数为11,方差为3
C.平均数为11,方差为2 D.平均数为12,方差为4
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13.已知实数![]() 、
、![]() 满足
满足![]() ,则
,则![]() _____.
_____.
14.已知菱形的两条对角线长为8cm和6cm,那么这个菱形的周长是______cm,面积是______cm1.
15.如图,△A1B1C1中,A1B1=4,A1C1=5,B1C1=1.点A2,B2,C2分别是边B1C1,A1C1,A1B1的中点;点A3,B3,C3分别是边B2C2,A2C2,A2B2的中点;…;以此类推,则第2019个三角形的周长是_____.

16.已知直线y=﹣![]() 与x轴、y轴分别交于点A、B,在坐标轴上找点P,使△ABP为等腰三角形,则点P的个数为_____个.
与x轴、y轴分别交于点A、B,在坐标轴上找点P,使△ABP为等腰三角形,则点P的个数为_____个.
17.分解因式:x2﹣7x=_____.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18.(5分)任丘市举办一场中学生乒乓球比赛,比赛的费用y(元)包括两部分:一部分是租用比赛场地等固定不变的费用b(元),另一部分费用与参加比赛的人数(x)人成正比.当x=20时,y=1600;当x=30时,y=1.
(1)求y与x之间的函数关系式;
(2)如果承办此次比赛的组委会共筹集;经费6350元,那么这次比赛最多可邀请多少名运动员参赛?
19.(5分)为了宣传2018年世界杯,实现“足球进校园”的目标,任城区某中学计划为学校足球队购买一批足球,已知购买2个A品牌的足球和3个B品牌的足球共需380元;购买4个A品牌的足球和2个B品牌的足球共需360元.
(1)求A,B两种品牌的足球的单价.
(2)学校准备购进这两种品牌的足球共50个,并且B品牌足球的数量不少于A品牌足球数量的4倍,请设计出最省钱的购买方案,求该方案所需费用,并说明理由.

20.(8分)计算:(1)2![]() ﹣6
﹣6![]() +3
+3![]() ;
;
(2)(![]() ﹣
﹣![]() )(
)(![]() +
+![]() )+(2
)+(2![]() ﹣3
﹣3![]() )2;
)2;
用指定方法解下列一元二次方程:
(3)x2﹣36=0(直接开平方法);
(4)x2﹣4x=2(配方法);
(5)2x2﹣5x+1=0(公式法);
(6)(x+1)2+8(x+1)+16=0(因式分解法)
21.(10分)某河道A,B两个码头之间有客轮和货轮通行![]() 一天,客轮从A码头匀速行驶到B码头,同时货轮从
一天,客轮从A码头匀速行驶到B码头,同时货轮从
B码头出发,运送一批建材匀速行驶到A码头![]() 两船距B码头的距离
两船距B码头的距离![]() 千米
千米![]() 与行驶时间
与行驶时间![]() 分
分![]() 之间的函数关系
之间的函数关系
如图所示![]() 请根据图象解决下列问题:
请根据图象解决下列问题:
![]() 分别求客轮和货轮距B码头的距离
分别求客轮和货轮距B码头的距离![]() 千米
千米![]() 、
、![]() 千米
千米![]() 与
与![]() 分
分![]() 之间的函数关系式;
之间的函数关系式;
![]() 求点M的坐标,并写出该点坐标表示的实际意义.
求点M的坐标,并写出该点坐标表示的实际意义.

22.(10分)问题背景:如图1:在四边形ABCD中,AB=AD,∠BAD=120∘ ,∠B=∠ADC=90°.E、F分别是 BC,CD 上的点.且∠EAF=60° . 探究图中线段BE,EF,FD 之间的数量关系. 小王同学探究此问题的方法是,延长 FD 到点 G,使 DG=BE,连结 AG,先证明△ABE≌△ADG, 再证明△AEF≌△AGF,可得出结论,他的结论应是_________;
探索延伸:如图2,若四边形ABCD中,AB=AD,∠B+∠D=180° .E,F 分别是 BC,CD 上的点,且∠EAF=![]() ∠BAD,上述结论是否仍然成立,并说明理由;
∠BAD,上述结论是否仍然成立,并说明理由;
实际应用:如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东 70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以55 海里/小时的速度前进,舰艇乙沿北偏东 50°的方向以 75 海里/小时的速度前进2小时后, 指挥中心观测到甲、乙两舰艇分别到达 E,F 处,且两舰艇之间的夹角为70° ,试求此时两舰 艇之间的距离.

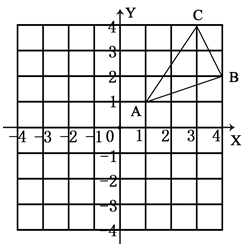
23.(12分)如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1) 请画出△ABC向左平移5个单位长度后得到的△A![]() B
B![]() C
C![]() ;
;
(2) 请画出△ABC关于原点对称的△A![]() B
B![]() C
C![]() ;
;
(3) 在![]() 轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.
轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.
参考答案
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、D
2、B
3、C
4、A
5、B
6、B
7、C
8、C
9、D
10、D
11、A
12、C
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13、3
14、10,14
15、![]()
16、1
17、x(x﹣7)
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18、 (1) 函数的解析式是:y=40x+800;(2) 这次比赛最多可邀请138名运动员.
19、(1)A品牌的足球的单价为40元,B品牌的足球的单价为100元(2)当a=10,即购买A品牌足球10个,B品牌足球40个,总费用最少,最少费用为4400元
20、(1)14![]() ;(2)31﹣12
;(2)31﹣12![]() ;(3)x1=﹣6,x2=6;(4)x1=2﹣
;(3)x1=﹣6,x2=6;(4)x1=2﹣![]() ,x2=2+
,x2=2+![]() ;(1)x1=
;(1)x1=![]() ,x2=
,x2=![]() ;(6)x1=x2=﹣1.
;(6)x1=x2=﹣1.
21、 (1)![]() ,
,![]() ;(2) 两船同时出发经24分钟相遇,此时距B码头8千米.
;(2) 两船同时出发经24分钟相遇,此时距B码头8千米.
22、问题背景:EF=BE+DF,理由见解析;探索延伸:结论仍然成立,理由见解析;实际应用:210海里.
23、(1)图形见解析;
(2)图形见解析;
(3)图形见解析,点P的坐标为:(2,0)
2022-2023学年贺州市重点中学数学七年级第二学期期末学业质量监测模拟试题含答案: 这是一份2022-2023学年贺州市重点中学数学七年级第二学期期末学业质量监测模拟试题含答案,共7页。试卷主要包含了考生要认真填写考场号和座位序号,一次函数,当时,x的取值范围是,下列命题的逆命题正确的是,下列方程中有一根为3的是等内容,欢迎下载使用。
2022-2023学年廊坊市重点中学数学七年级第二学期期末监测模拟试题含答案: 这是一份2022-2023学年廊坊市重点中学数学七年级第二学期期末监测模拟试题含答案,共8页。试卷主要包含了下列说法正确的是,下列各组数中,不是勾股数的是等内容,欢迎下载使用。
2022-2023学年山南市重点中学数学七年级第二学期期末监测试题含答案: 这是一份2022-2023学年山南市重点中学数学七年级第二学期期末监测试题含答案,共7页。试卷主要包含了若分式有意义,则的取值范围为,下列说法等内容,欢迎下载使用。












