2022-2023学年福建省惠安科山中学数学七下期末调研试题含答案

2022-2023学年福建省惠安科山中学数学七下期末调研试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项：

1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。回答非选择题时，将答案写在答题卡上，写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交回。

一、选择题(每小题3分,共30分)

1．无理数2﹣3在（　　）

A．2和3之间 B．3和4之间 C．4和5之间 D．5和6之间

2．在式子，，，，，中，分式的个数有（    ）

A．2 B．3 C．4 D．5

3．如图，在一个高为6米，长为10米的楼梯表面铺地毯，则地毯长度至少是（    ）

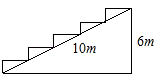
A．6米 B．10米 C．14米 D．16米

4．下列计算错误的是（　　）

A． =2 B．=3 C．÷=3 D．=1﹣=

5．把多项式ax3﹣2ax2+ax分解因式，结果正确的是（　　）

A．ax（x2﹣2x） B．ax2（x﹣2）

C．ax（x+1）（x﹣1） D．ax（x﹣1）2

6．菱形ABCD的对角线AC＝6cm，BD＝4cm，以AC为边作正方形ACEF，则BF长为(　　)

A．4cm B．5cm C．5cm或8cm D．5cm或cm

7．若以二元一次方程x+2y﹣b=0的解为坐标的点（x，y）都在直线y=﹣x+b﹣l上，则常数b=（　　）

A． B．2 C．﹣1 D．1

8．菱形的两条对角线长为6 cm 和8 cm，那么这个菱形的周长为

A．40 cm B．20 cm C．10 cm D．5 cm

9．如图，在△ABC中,BC=5，AC=8,AB的垂直平分线交AB于点D,交AC于点E,则△BCE的周长等于（    ）

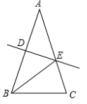
A．18 B．15 C．13 D．12

10．不等式 的正整数解的个数是（  ）

A．7个 B．6个 C．4个 D．0个

二、填空题(本大题共有6小题，每小题3分，共18分)

11．已知一个直角三角形斜边上的中线长为6 cm，那么这个直角三角形的斜边长为______cm.

12．若二次根式在实数范围内有意义，则x的取值范围是_____．

13． “今有井径五尺，不知其深，立五尺木于井上，从木末望水岸，入径四寸，问井深几何？”这是我国古代数学《九章算术》中的“井深几何”问题，它的题意可以由图获得，则井深为_____尺．

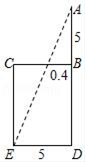
14．已知一次函数y=bx+5和y=﹣x+a的图象交于点P（1，2），直接写出方程的解_____．

15．对于实数x，我们[x]表示不大于x的最大整数，例如[1.2]＝1，[3]＝3，[﹣2.5]＝﹣3，若[]＝5，则x的取值范围是______．

16．将直线向上平移个单位后，可得到直线_______.

三、解下列各题(本大题共8小题，共72分)

17．（8分）如图：是某出租车单程收费y(元)与行驶路程x(千米)之间的函数关系图象,根据图象回答下列问题：

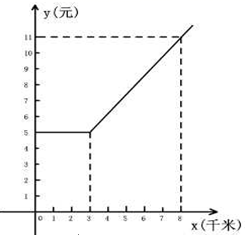
（1）当行使8千米时,收费应为       元；

（2）从图象上你能获得哪些信息?(请写出2条)

①                   ________

②____________________________

（3）求出收费y(元)与行使x(千米)(x≥3)之间的函数关系式.

18．（8分）如图所示，直线y＝－x＋8与x轴、y轴分别相交于点A，B，设M是OB上一点，若将△ABM沿AM折叠，使点B恰好落在x轴上的点B′处．

求：(1)点B′的坐标；

(2)直线AM所对应的函数表达式．

19．（8分）阅读材料，回答问题：

材料：将一个多项式分组后，可提公因式或运用公式继续分解的方法是因式分解中的分组分解法，一般的分组分解法有四种形式，即“”分法、“”分法、“”分法及“”分法等．

如“”分法：

请你仿照以上方法，探索并解决下列问题：

分解因式：（1）；

（2）．

20．（8分）某市为鼓励市民节约用水，自来水公司按分段收费标准收费，如图反映的是每月水费（元）与用水量（吨）之间的函数关系.

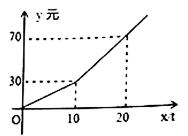
（1）当用水量超过10吨时，求关于的函数解析式（不必写自变量取值范围）；

（2）按上述分段收费标准小聪家三、四月份分别交水费38元和27元，问四月份比三月份节约用水多少吨？

21．（8分）如图,BD是△ABC的角平分线,点E,F分别在BC、AB上,且DE∥AB,EF∥AC．

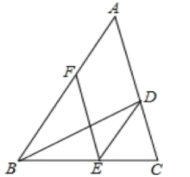
(1)求证：BE=AF；

(2)若∠ABC=60°，BD=6，求四边形ADEF的面积。

22．（10分）已知：如图，，，求的面积．

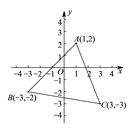
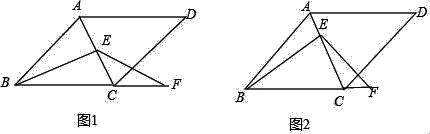
23．（10分）在菱形ABCD中，∠ABC=60°，E是对角线AC上任意一点，F是线段BC延长线上一点，且CF=AE，连接BE、EF．

（1）如图1，当E是线段AC的中点时，求证：BE=EF．

（2）如图2，当点E不是线段AC的中点，其它条件不变时，请你判断（1）中的结论是否成立？若成立，请证明；若不成立，说明理由．

24．（12分）计算：（1）

（2）（﹣1）2﹣（﹣）（+）

参考答案

一、选择题(每小题3分,共30分)

1、B

2、B

3、C

4、D

5、D

6、D

7、B

8、B

9、C

10、B

二、填空题(本大题共有6小题，每小题3分，共18分)

11、1

12、x＞2019

13、57.5

14、．

15、46≤x<1

16、

三、解下列各题(本大题共8小题，共72分)

17、（1）11；（2）如：出租车起步价（3千米内）为5元；超出3千米，每千米加收1.2元等；（3）.

18、（1）点B′的坐标为(－4，0)；（2）直线AM的函数表达式为y＝－x＋3.

19、（1）；（2）

20、（1）；（2）四月份比三月份节约用水3吨.

21、（1）详见解析；（2）

22、14

23、 (1)详见解析；（2）结论成立，理由详见解析.

24、（1）；（2）