【同步练习】高中数学人教A版(2019)必修第二册--6.4.2向量在物理中的应用举例 课时作业（含解析）

6．4.1　平面几何中的向量方法6．4.2　向量在物理中的应用举例

必备知识基础练　

1．人骑自行车的速度是v1，风速为v2，则逆风行驶的速度为(　　)

A．v1－v2    B．v1＋v2C．|v1|－|v2|    D．||

2．一物体在力F的作用下，由点A(10，5)移动到点B(4，2)，已知F＝(3，－5)，则F对该物体所做的功为(　　)

A．6    B．－6

C．3    D．－3

3．设O为△ABC的重心，M为△ABC所在平面内任意一点，则＋＋＝(　　)

A．0    B．C．2    D．3

4．在△ABC中，若·＋2＝0，则△ABC的形状是(　　)

A．∠C为钝角的三角形

B．∠B为直角的直角三角形

C.锐角三角形

D．∠A为直角的直角三角形

5．P是△ABC所在平面内一点，若＝3＋，则S△ABP∶S△ABC＝(　　)

A．1∶4    B．1∶3

C．2∶3    D．2∶1

6．(多选)在水流速度为10 km/h的自西向东的河中，如果要使船以10 km/h的速度与河的南岸垂直到达北岸，则船出发时行驶速度的大小与方向为(　　)

A．北偏西30°    B．北偏西60°

C．20 km/h    D．30 km/h

7．在直角梯形ABCD中，AB⊥AD，AB＝2，DC＝1，AB∥DC，则当AC⊥BC时，AD＝________．

8．在四边形ABCD中，＝(3，－1)，＝(2，m)，⊥，则该四边形的面积是________．

关键能力综合练　

1．已知在四边形ABCD中，＝－a－2b，＝4a＋b，＝5a＋3b，则四边形ABCD的形状是(　　)

A．矩形    B．梯形

C．平行四边形    D．以上都不对

2．在△ABC中，设2－2＝2·，那么动点M的轨迹必通过△ABC的(　　)

A．垂心    B．内心

C．外心    D．重心

3．在△ABC中，若·＝·，则△ABC的形状为(　　)

A．等边三角形    B．等腰三角形

C．直角三角形    D．等腰直角三角形

4．已知△ABC是边长为2的等边三角形，P为平面ABC内一点，则·(＋)的最小值是(　　)

A．－2　　　B．－    C．－　　　D．－1

5．(多选)已知△ABC的重心为O，边AB，BC，CA的中点分别为D，E，F，则(　　)

A．＋＝2

B．＋＝

C．若·(－)＝0，则OA⊥BC

D．若△ABC为正三角形，则·＋·＋·＝0

6．(多选)一物体受到3个力的作用，其中重力G的大小为4 N，水平拉力F1的大小为3 N，另一力F2未知，则(　　)

A．当该物体处于平衡状态时，|F2|＝5 N

B．当F2与F1方向相反，且|F2|＝5 N时，物体所受合力大小为0

C．当物体所受合力为F1时，|F2|＝4 N

D．当|F2|＝2 N时，3 N≤|F1＋F2＋G|≤7 N

7．已知O是△ABC内一点，且满足(＋)·＝(＋)·＝0，若AC＝，则·＝________．

8．点P是边长为2的正三角形ABC的三条边上任意一点，则|＋＋|的最小值为________．

9．已知四边形ABCD的四个顶点分别为A(1，0)，B(7，3)，C(4，4)，D(2，3).

(1)求向量与夹角的余弦值；

(2)证明：四边形ABCD是等腰梯形．

10.

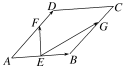
如图，在平行四边形ABCD中，点E是AB的中点，F，G是AD，BC的三等分点(AF＝AD，BG＝BC).设＝a，＝b.

(1)用a，b表示，；

(2)如果|a|＝|b|，用向量的方法证明：EF⊥EG.

核心素养升级练　

1．在平面上有△ABC及内一点O满足关系式：S△OBC·＋S△OAC·＋S△OAB·＝0即称为经典的“奔驰定理”，若△ABC的三边为a，b，c，现有a·＋b·＋c·＝0，则O为△ABC的(　　)

A．外心　　B．内心　　C．重心　　D．垂心

2．已知在平面内，向量|a|＝|b|＝2，〈a，b〉＝120°，〈a－c，b－c〉＝60°，则|c|的最大值为______，|c|的最小值为________．

3.

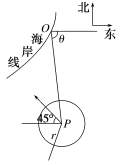
在某海滨城市O附近海面有一台风，据监测，当前台风中心位于城市O(如图所示)的东偏南θ(cos θ＝，θ∈(0°，90°))方向300 km的海面P处，并以20 km/h的速度向西偏北45°方向移动．台风侵袭的范围为圆形区域，当前半径为60 km，并以10 km/h的速度不断增大．问几小时后该城市开始受到台风的侵袭？注：cos (θ－45°)＝.

6．4.1　平面几何中的向量方法

6．4.2　向量在物理中的应用举例

必备知识基础练

1．答案：A

解析：由向量的加法法则可得逆风行驶的速度为v1－v2.注意速度是有方向和大小的，是一个向量．故选A.

2．答案：D

解析：∵A(10，5)，B(4，2)∴＝(－6，－3)，又∵F＝(3，－5)，∴F·＝－6×3＋(－3)×(－5)＝－3.故选D.

3．答案：D

解析：由题意得：在△ABC中，＋＋＝0，＋＋＝＋＋＋＋＋＝3.故选D.

4．答案：D

解析：在△ABC中，·＋2＝·(＋)＝·＝0，∴⊥，∴∠A＝，则△ABC为直角三角形，故选D.

5．答案：A

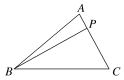
解析：由题设，3＝＋＝，故C，P，A共线且CP＝3PA，如图所示，所以S△ABP∶S△ABC＝1∶4.故选A.

6．答案：AC

解析：

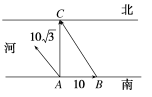
如图所示，设||＝10，||＝10，所以||＝＝20，

而tan ∠CBA＝，所以∠CBA＝60°，即船出发时行驶速度的大小为20 km/h，方向为北偏西30°.故选AC.

7．答案：1

解析：

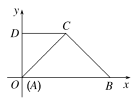
建立如图的平面直角坐标系，则A(0，0)，B(2，0).设AD＝a，则C(1，a)，＝(1，a)，＝(－1，a).因为AC⊥BC，所以⊥.所以·＝－1＋a2＝0，所以a＝1(负值舍去).

8．答案：10

解析：因为＝(3，－1)，＝(2，m)，⊥，所以·＝3×2＋(－1)m＝0，即m＝6，所以四边形的面积为＝＝10.

关键能力综合练

1．答案：B

解析：

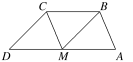
＝－a－2b，＝4a＋b，＝5a＋3b，则－＝＋＝5a＋3b＝.设＋＝，故BCDM，ABCM为平行四边形，故ABCD为梯形．故选B.

2．答案：C

解析：

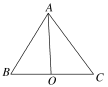
设BC的中点是O，2－2＝(＋)·(－)＝2·＝2·，即(－)·＝·＝0，所以⊥，所以动点M在线段BC的中垂线上，故动点M的轨迹必通过△ABC的外心，故选C.

3．答案：B

解析：

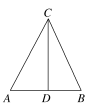
取AB中点D，连接CD，则＋＝2，因为·＝·，所以·－·＝0，所以·＋·＝·(＋)＝2·＝0，所以⊥，即AB⊥DC，所以△ABC的是等腰三角形．故选B.

4．答案：B

解析：

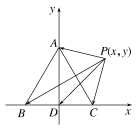
建立如图所示的坐标系，以BC的中点为坐标原点，则A(0，)，B(－1，0)，C(1，0)，设P(x，y)，则＝(－x，－y)，＝(－1－x，－y)，＝(1－x，－y)，则·(＋)＝2x2－2y＋2y2＝2[x2＋(y－)2－]，∴当x＝0，y＝时，取得最小值2×＝－，故选B.

5．答案：ABC

解析：对于A，因为D为△OAB中AB的中点，所以＋＝2，故A正确；对于B，因为O为△ABC的重心，D，E，F分别为边AB，BC，CA的中点，所以＋＋＝(＋)＋(＋)＋(＋)＝＋＋＝2＋＝0，所以＋＝，故B正确；对于C，因为·(－)＝·＝0，所以OA⊥BC，所以C正确；对于D，因为△ABC为正三角形，所以·＝||2cos 120°＝－|OA|2，所以·＋·＋·＝－||2，所以D不正确．故选ABC.

6．答案：ACD

解析：A选项：由题知，F2的大小等于重力G与水平拉力F1的合力大小，由图知|F2|＝5 N，故A正确；

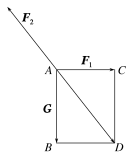
B选项：如图，物体所受合力大小应等于向量与F2的和向量的大小，显然B错误；

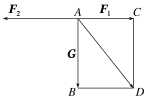
C选项；当物体所受合力为F1时，说明G与F2的合力为0，所以|F2|＝4 N，C正确；

D选项：由上知，重力G与水平拉力F1的合力为，||＝5 N，易知当F2与同向时合力最大，最大值为7 N，反向时合力最小，最小值为3 N，即3 N≤|F1＋F2＋G|≤7 N，故D正确．故选ACD.

7．答案：－1

解析：由题意得(＋)·(－)＝(＋)·(－)＝0，则||＝||＝||，O是△ABC的外心，故·＝－2＝－1.

8．答案：

解析：

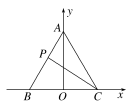
不妨假设P在AB上且A(0，)，B(－1，0)，C(1，0)，如图所示，所以，P在y＝(x＋1)上且－1≤x≤0，设P(x，(x＋1))，

则＝(－x，－x)，

＝(－1－x，－(x＋1))，＝(1－x，－(x＋1))，所以＋＋＝(－3x，－3x－2)，故|＋＋|＝ ＝ ，

当x＝－时，|＋＋|的最小值为.

9．解析：(1)因为＝(7，3)－(1，0)＝(6，3)，＝(4，4)－(1，0)＝(3，4)，

所以cos 〈，〉＝＝＝.

(2)证明：因为＝(4，4)－(2，3)＝(2，1)，所以＝3，即AB∥CD，

而＝(4，4)－(7，3)＝(－3，1)，＝(2，3)－(1，0)＝(1，3)，故不存在λ∈R使＝λ，即BC，AD不平行，

又||＝，||＝，故||＝||，

综上，四边形ABCD是等腰梯形．

10．解析：(1)因为点E是AB的中点，所以＝＝＝a.

因为AF＝AD，BG＝BC，所以＝＝＝b.

所以＝－＝b－a，＝＋＝a＋b.

(2)证明：由(1)可得：＝b－a，＝a＋b.

因为|a|＝|b|，

所以·＝(b－a)·(b＋a)＝|b|2－|a|2＝|b|2－(|b|)2＝0，

所以EF⊥EG.

核心素养升级练

1．答案：B

解析：记点O到AB、BC、CA的距离分别为h1，h2，h3，S△OBC＝a·h2，S△OAC＝b·h3，S△OAB＝c·h1，因为S△OBC·＋S△OAC·＋S△OAB·＝0，则a·h2·＋b·h3·＋c·h1·＝0，即a·h2·＋b·h3·＋c·h1·＝0，又因为a·＋b·＋c·＝0，所以h1＝h2＝h3，所以点P是△ABC的内心．故选B.

2．答案：4　2

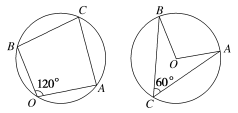
解析：设＝a，＝b，＝c，所以＝a－c，＝b－c，∠AOB＝120°，∠ACB＝60°.即∠ACB＋∠AOB＝180°.根据圆的性质，可能出现如下两种圆的图形，当A，O，B，C四点共圆时，此时OA＝OB＝2，AB＝2，2R＝＝4，OC＝|c|∈(OA，2R]＝(2，4]，当A，B，C三点在以O为圆心半径为2的圆上时，OC＝|c|＝2.综上，OC＝|c|∈[2，4]，即最大值为4，最小值为2.

3．解析：设t h后，台风中心移动到Q处，此时城市开始受到台风的侵袭，

∠OPQ＝θ－45°.

∵＝＋，

∴2＝(＋)2＝2＋2＋2·.

∴2＝2＋2－2||||cos (θ－45°)＝3002＋(20t)2－2×300×20t×＝100(4t2－96t＋900).

依题意得2≤(60＋10t)2，解得12≤t≤24.

从而12 h后该城市开始受到台风的侵袭．