


2022-2023学年福建省仙游第一中学数学七年级第二学期期末学业水平测试试题含答案
展开2022-2023学年福建省仙游第一中学数学七年级第二学期期末学业水平测试试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题(每小题3分,共30分)
1.下列一元二次方程中,有两个不相等实数根的是()
A.![]() B.
B.![]()
C.![]() D.
D.![]()
2.如图,直角梯形 ABCD 中,AD∥BC,AB⊥BC,AD=3,BC=1.将腰 CD 以 D 为旋转中心逆时针旋转 90°至 DE,连结 AE,则△ADE 的面积是( )
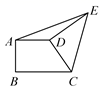
A.![]() B.2 C.
B.2 C.![]() D.不能确定
D.不能确定
3.如图所示,已知四边形ABCD是平行四边形,下列结论中,不一定正确的是( )
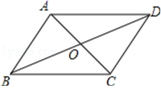
A.△AOB的面积等于△AOD的面积 B.当AC⊥BD时,它是菱形
C.当OA=OB时,它是矩形 D.△AOB的周长等于△AOD的周长
4.下列说法错误的是( )
A.一组对边平行且相等的四边形是平行四边形 B.四条边都相等的四边形是菱形
C.对角线互相垂直的平行四边形是正方形 D.四个角都相等的四边形是矩形
5.甲、乙、丙、丁四人进行射击测试,每人射击10次,四人的平均成绩均是9.4环,方差分别是0.43,1.13,0.90,1.68,则在本次射击测试中,成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁
6.已知多边形的内角和等于外角和,这个多边形的边数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.在平面直角坐标系中,一矩形上各点的纵坐标不变,横坐标变为原来的![]() ,则该矩形发生的变化为( )
,则该矩形发生的变化为( )
A.向左平移了![]() 个单位长度 B.向下平移了
个单位长度 B.向下平移了![]() 个单位长度
个单位长度
C.横向压缩为原来的一半 D.纵向压缩为原来的一半
8.下列各式中属于最简二次根式的是( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.关于![]() 的一元二次方程
的一元二次方程![]() 有两个不相等的实数根,则
有两个不相等的实数根,则![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() 且
且![]() D.
D.![]() 且
且![]()
10.下列运算错误的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
二、填空题(本大题共有6小题,每小题3分,共18分)
11.如图,点A在反比例函数![]() 的图像上,AB⊥x轴,垂足为B,且
的图像上,AB⊥x轴,垂足为B,且![]() ,则
,则![]() _____ .
_____ .

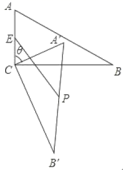
12.如图,在![]() 中,
中,![]() ,将
,将![]() 绕顶点
绕顶点![]() 顺时针旋转,旋转角为
顺时针旋转,旋转角为![]() ,得到
,得到![]() .设
.设![]() 中点为
中点为![]() ,
,![]() 中点为
中点为![]() ,
,![]() ,连接
,连接![]() ,当
,当![]() ____________
____________![]() 时,
时,![]() 长度最大,最大值为____________.
长度最大,最大值为____________.
13.化简;![]() ÷(
÷(![]() ﹣1)=______.
﹣1)=______.
14.在设计人体雕像时,使雕像的上部(腰以上)与下部(腰以下)的高度比,等于下部与全部(全身)的高度比,可以增加视觉美感.按此比例,如果雕像的高度为 1m,那么它的下部应设计的高度为_____.
15.将直线y=﹣4x+3向下平移4个单位,得到的直线解析式是_____.
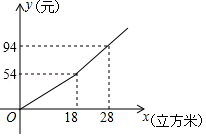
16.某市规定了每月用水不超过l8立方米和超过18立方米两种不同的收费标准,该市用户每月应交水费y(元)是用水x(立方米)的函数,其图象如图所示.已知小丽家3月份交了水费102元,则小丽家这个月用水量为_____立方米.
三、解下列各题(本大题共8小题,共72分)
17.(8分)青岛市某大酒店豪华间实行淡季、旺季两种价格标准,旺季每间价格比淡季上涨![]() .下表是去年该酒店豪华间某两天的相关记录:
.下表是去年该酒店豪华间某两天的相关记录:
| 淡季 | 旺季 |
未入住房间数 | 10 | 0 |
日总收入(元) | 24000 | 40000 |
酒店豪华间有多少间?旺季每间价格为多少元?
18.(8分)在学校组织的“学习强国”知识竞赛中,每班参加比赛的人数相同,成绩分为![]() ,
,![]() ,
,![]() ,
,![]() 四个等级其中相应等级的得分依次记为
四个等级其中相应等级的得分依次记为![]() 分,
分,![]() 分,
分,![]() 分和
分和![]() 分.年级组长张老师将
分.年级组长张老师将![]() 班和
班和![]() 班的成绩进行整理并绘制成如下的统计图:
班的成绩进行整理并绘制成如下的统计图:
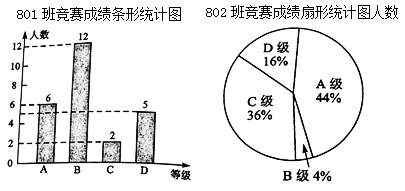
(1)在本次竞赛中,![]() 班
班![]() 级的人数有多少。
级的人数有多少。
(2)请你将下面的表格补充完整:
成绩 班级 | 平均数(分) | 中位数 (分) | 众数 (分) | B级及以上人数 |
|
|
|
|
|
|
|
|
|
|
(3)结合以上统计量,请你从不同角度对这次竞赛成绩的结果进行分析(写出两条)
19.(8分)下面是小东设计的“作矩形”的尺规作图过程,已知:![]()
求作:矩形![]()
作法:如图,
①作线段![]() 的垂直平分线角交
的垂直平分线角交![]() 于点
于点![]() ;
;
②连接![]() 并延长,在延长线上截取
并延长,在延长线上截取![]()
③连接![]()
所以四边形![]() 即为所求作的矩形
即为所求作的矩形
根据小东设计的尺规作图过程
(1)使用直尺和圆规,补全图形:(保留作图痕迹)
(2)完成下边的证明:
证明:![]() ,
,![]() ,
,
![]() 四边形是平行四边形( )(填推理的依据)
四边形是平行四边形( )(填推理的依据)
![]()
![]() 四边形
四边形![]() 是矩形( )(填推理的依据)
是矩形( )(填推理的依据)
20.(8分)四边形ABCD是正方形,AC与BD,相交于点O,点E、F是直线AD上两动点,且AE=DF,CF所在直线与对角线BD所在直线交于点G,连接AG,直线AG交BE于点H.
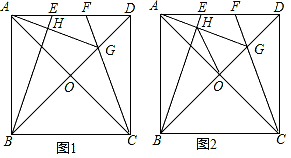
(1)如图1,当点E、F在线段AD上时,求证:∠DAG=∠DCG;
(2)如图1,猜想AG与BE的位置关系,并加以证明;
(3)如图2,在(2)条件下,连接HO,试说明HO平分∠BHG.
21.(8分)先化简,再求值:![]() ,其中
,其中![]() 是
是![]() 中的一个正整数解.
中的一个正整数解.
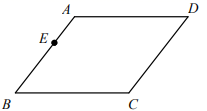
22.(10分)如图,平行四边形ABCD中,点E为AB边上一点,请你用无刻度的直尺,在CD边上画出点 F,使四边形AECF为平行四边形,并说明理由.
23.(10分)我市某林场计划购买甲、乙两种树苗共800株,甲种树苗每株24元,乙种树苗每株30元.相关资料表明:甲、乙两种树苗的成活率分别为85%、90%.
(1)若购买这两种树苗共用去21000元,则甲、乙两种树苗各购买多少株?
(2)若要使这批树苗的总成活率不低于88%,则甲种树苗至多购买多少株?
(3)在(2)的条件下,应如何选购树苗,使购买树苗的费用最低?并求出最低费用.
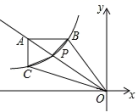
24.(12分)如图,已知点A的坐标为(a,4)(其中a<-3),射线OA与反比例函数![]() 的图象
的图象![]() 交于点P,点B,C分别在函数
交于点P,点B,C分别在函数![]() 的图象上,且AB∥x轴,AC∥y轴,连结BO,CO,BP,CP.
的图象上,且AB∥x轴,AC∥y轴,连结BO,CO,BP,CP.
(1)当a=-6,求线段AC的长;
(2)当AB=BO时,求点A的坐标;
(3)求证:![]() .
.
参考答案
一、选择题(每小题3分,共30分)
1、B
2、A
3、D
4、C
5、A
6、B
7、C
8、B
9、D
10、A
二、填空题(本大题共有6小题,每小题3分,共18分)
11、1
12、![]() 3
3
13、-![]()
14、![]()
15、y=﹣4x﹣1
16、1
三、解下列各题(本大题共8小题,共72分)
17、该酒店豪华间有50间,旺季每间价格为800元.
18、(1)9人;(2)见解析;(3)略.
19、(1)见解析;(2)OC,对角线互相平分的四边形是平行四边形;一角为直角的平行四边形是矩形.
20、(1)证明见解析(2)AG⊥BE(3)证明见解析
21、化简为![]() ,当x=3时,此时的值为-10.
,当x=3时,此时的值为-10.
22、见详解.
23、(1)购买甲种树苗500株,乙种树苗300株(2)320株(3)当选购甲种树苗320株,乙种树苗480株时,总费用最低,为22080元
24、(1)![]() ;(2)
;(2)![]() ;(3)见解析
;(3)见解析








