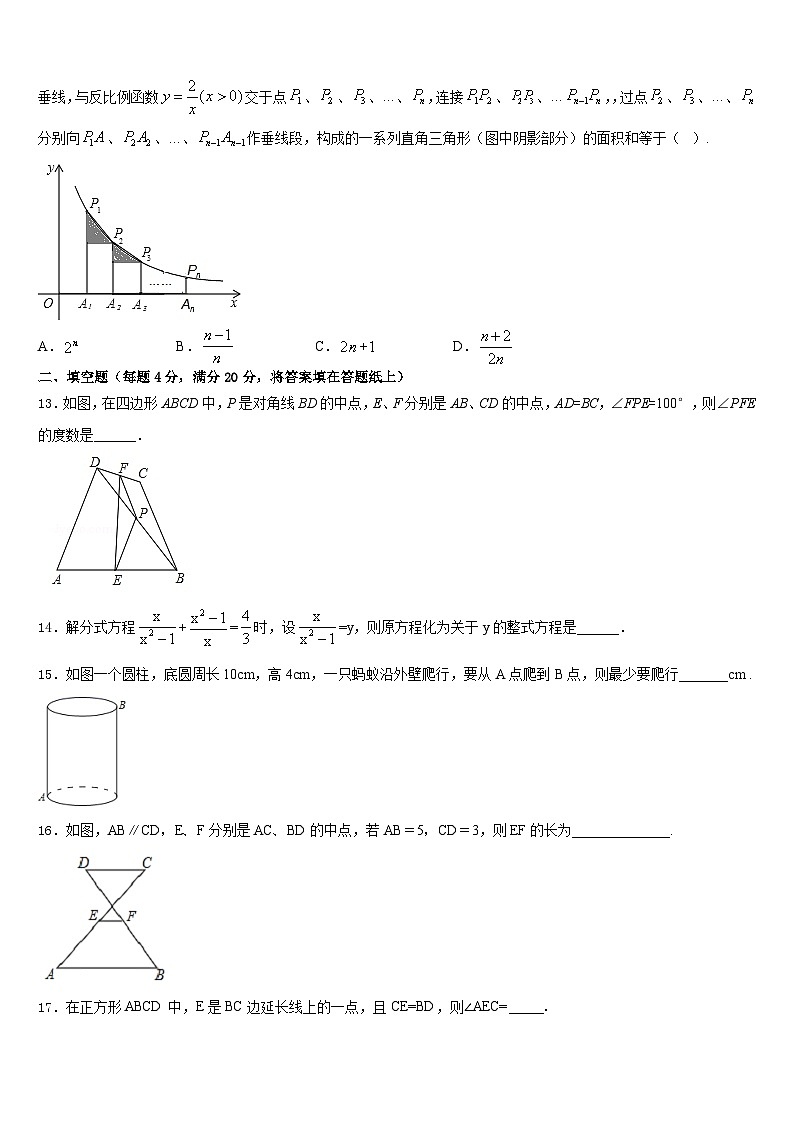
2022-2023学年浙江省杭州市拱墅区数学七年级第二学期期末学业水平测试模拟试题含答案

2022-2023学年浙江省杭州市拱墅区数学七年级第二学期期末学业水平测试模拟试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项:

1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内。

2．答题时请按要求用笔。

3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效。

4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。

5．保持卡面清洁，不要折暴、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1．下列各式：（1﹣x），，，，其中分式共有（　　）

A．1个 B．2个 C．3个 D．4个

2．如图所示，已知四边形ABCD是平行四边形，下列结论中，不一定正确的是（　　）

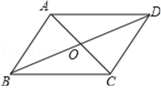
A．△AOB的面积等于△AOD的面积 B．当AC⊥BD时，它是菱形

C．当OA=OB时，它是矩形 D．△AOB的周长等于△AOD的周长

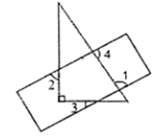
3．一直尺与一个锐角为角的三角板如图摆放，若，则的度数为（  ）

A． B． C． D．

4．如果一个多边形的每一个外角都是60°，则这个多边形的边数是（ ）

A．3 B．4 C．5 D．6

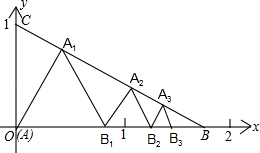
5．如图所示，已知：点A（0，0），B（，0），C（0，1）．在△ABC内依次作等边三角形，使一边在x轴上，另一个顶点在BC边上，作出的等边三角形分别是第1个△AA1B1，第2个△B1A2B2，第3个△B2A3B3，…，则第n个等边三角形的边长等于（　　）

A． B． C． D．

6．已知正比例函数y＝（m﹣1）x的图象上两点A（x1，y1），B（x2，y2），当x1＜x2时，有y1＞y2，那么m的取值范围是（　　）

A．m＜1 B．m＞1 C．m＜2 D．m＞0

7．已知点(-2，y1)，(-1，y2)，(4，y3)在函数y=的图象上，则(   )

A．y2<y1<y3 B．y1<y2<y3 C．y3<y1<y2 D．y3<y2<y1

8．下列各式中，从左到右的变形是因式分解的是（　　）

A．2a2﹣2a+1=2a（a﹣1）+1 B．（x+y）（x﹣y）=x2﹣y2

C．x2﹣6x+5=（x﹣5）（x﹣1） D．x2+y2=（x﹣y）2+2x

9．下列各组条件中，不能判定四边形是平行四边形的是（    ）

A．， B．，

C．， D．，

10．若，则代数式的值是（　　　　）

A．9 B．7 C． D．1

11．如图，△ABC中，∠A=30°，∠ACB=90°，BC=2，D是AB上的动点，将线段CD绕点C逆时针旋转90°，得到线段CE，连接BE，则BE的最小值是（       ）

A．-1 B． C． D．2

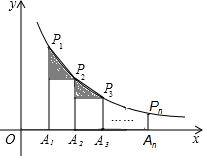
12．如图，在轴正半轴上依次截取，过点、、、……分别作轴的垂线，与反比例函数交于点、、、…、，连接、、…，，过点、、…、分别向、、…、作垂线段，构成的一系列直角三角形（图中阴影部分）的面积和等于（  ）.

A． B． C． D．

二、填空题（每题4分，满分20分，将答案填在答题纸上）

13．如图，在四边形ABCD中，P是对角线BD的中点，E、F分别是AB、CD的中点，AD=BC，∠FPE=100°，则∠PFE的度数是______．

14．解分式方程+=时，设=y，则原方程化为关于y的整式方程是______．

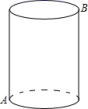
15．如图一个圆柱，底圆周长10cm，高4cm，一只蚂蚁沿外壁爬行，要从A点爬到B点，则最少要爬行_______cm .

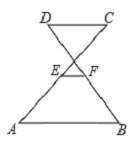
16．如图，AB∥CD，E、F分别是AC、BD的中点，若AB＝5，CD＝3，则EF的长为______________.

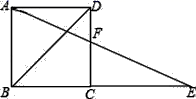
17．在正方形ABCD中，E是BC边延长线上的一点，且CE=BD，则∠AEC=_____．

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18．（5分）先化简，再求值:  ，其中x=

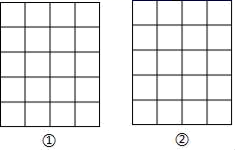
19．（5分）如图，正方形网格中，每个小正方形的边长均为1，每个小正方形的顶点叫格点，以格点为顶点按下列要求画图：

（1）在图①中画一条线段AB，使AB＝ ；

（2）在图②中画一个以格点为顶点，面积为2的正方形ABCD．

20．（8分）如图，已知E，F分别是▱ABCD的边BC、AD上的点，且BE=DF

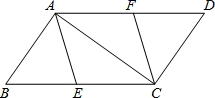
求证：四边形AECF是平行四边形．

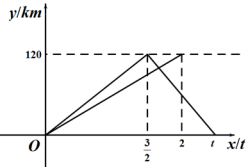
21．（10分）一辆轿车从甲地驶往乙地，到达乙地后立即返回甲地，速度是原来的1.5倍，往返共用t小时.一辆货车同时从甲地驶往乙地，到达乙地后停止.两车同时出发，匀速行驶，设轿车行驶的时间为x（h），两车离开甲地的距离为y（km），两车行驶过程中y与x之间的函数图象如图所示.

（1）轿车从乙地返回甲地的速度为        km/t，t=        h ；

（2）求轿车从乙地返回甲地时y与x之间的函数关系式；

（3）当轿车从甲地返回乙地的途中与货车相遇时，求相遇处到甲地的距离.

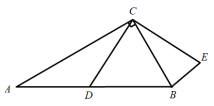
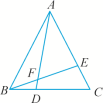
22．（10分）如图，△ABC是等边三角形，点D，E分别在BC，AC上，且BD=CE，AD与BE相交于点F.

（1）试说明△ABD≌△BCE；

（2）△AEF与△BEA相似吗？请说明理由；

（3）BD2=AD·DF吗？请说明理由．

23．（12分）解不等式组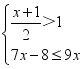，并在数轴上把解集表示出来．

参考答案

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1、A

2、D

3、C

4、D

5、A

6、A

7、A

8、C

9、B

10、D

11、A

12、B

二、填空题（每题4分，满分20分，将答案填在答题纸上）

13、40°。

14、y2-y+1=1

15、

16、1

17、22.5°

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18、，

19、（1）详见解析；（2）详见解析．

20、证明见解析．

21、 (1) 120； ;(2) y=-120x+300; (3) 100km.

22、 (1)见解析；(2)见解析；(3)见解析；

23、x＞1