


黑龙江省大庆市三站中学2022-2023学年七年级数学第二学期期末学业水平测试试题含答案
展开黑龙江省大庆市三站中学2022-2023学年七年级数学第二学期期末学业水平测试试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
考生请注意:
1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。
2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。
3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。
一、选择题(每小题3分,共30分)
1.如图,在平面直角坐标系中,点![]() 是直线
是直线![]() 上一点,过
上一点,过![]() 作
作![]() 轴,交直线
轴,交直线![]() 于点
于点![]() ,过
,过![]() 作
作![]() 轴,交直线
轴,交直线![]() 于点
于点![]() ,过
,过![]() 作
作![]() 轴交直线
轴交直线![]() 于点
于点![]()
![]() ,依次作下去,若点
,依次作下去,若点![]() 的纵坐标是1,则
的纵坐标是1,则![]() 的纵坐标是( ).
的纵坐标是( ).
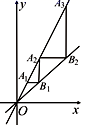
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.如图,正方形ABCD的边长为1,点E,F分别是对角线AC上的两点,EG⊥AB.EI⊥AD,FH⊥AB,FJ⊥AD,垂足分别为G,I,H,J.则图中阴影部分的面积等于 ( )
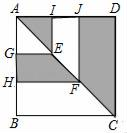
A.1 B.![]() C.
C.![]() D.
D.![]()
3.如图,函数 y1=﹣2x 与 y2=ax+3 的图象相交于点 A(m,2),则关于 x 的不等式﹣2x>ax+3 的解集是( )
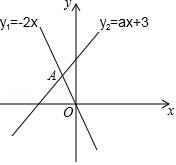
A.x>2 B.x<2 C.x>﹣1 D.x<﹣1
4.如图,四边形ABCD中,AB=CD,对角线AC,BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连接AF,CE,若DE=BF,则下列结论:①CF=AE;②OE=OF;③四边形ABCD是平行四边形;④图中共有四对全等三角形.其中正确结论的个数是
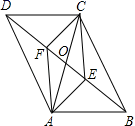
A.4 B.3 C.2 D.1
5.如图,在平面直角坐标系xOy中,点P(1,0).点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(﹣1,1),第3次向上跳动1个单位至点P3,第4次向右跳动3个单位至点P4,第5次又向上跳动1个单位至点P5,第6次向左跳动4个单位至点P6,….照此规律,点P第100次跳动至点P100的坐标是( )
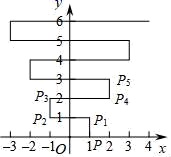
A.(﹣26,50) B.(﹣25,50)
C.(26,50) D.(25,50)
6.如图,![]() 两地被池塘隔开,小明先在直线
两地被池塘隔开,小明先在直线![]() 外选一点
外选一点![]() ,然后测量出
,然后测量出![]() ,
,![]() 的中点
的中点![]() ,并测出
,并测出![]() 的长为
的长为![]() .由此,他可以知道
.由此,他可以知道![]() 、
、![]() 间的距离为( )
间的距离为( )
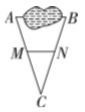
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.如图,平行四边形ABCD的对角线AC、BD相交于点O,已知AD=5,BD=8,AC=6,则△OBC的面积为( )
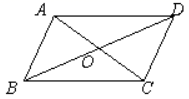
A.5 B.6 C.8 D.12
8.如图,四边形ABCD中,对角线相交于点O,E、F、G、H分别是AD、BD、BC、AC的中点,要使四边形EFGH是矩形,则四边形ABCD需要满足的条件是![]()
![]()
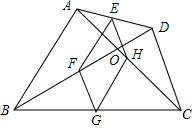
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.如图,菱形![]() 的对角线
的对角线![]() 、
、![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,则
,则![]() 的长为( )
的长为( )
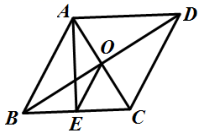
A.![]() B.2 C.3 D.6
B.2 C.3 D.6
10.二次根式![]() 中x的取值范围是( )
中x的取值范围是( )
A.x≥5 B.x≤5 C.x≥﹣5 D.x<5
二、填空题(本大题共有6小题,每小题3分,共18分)
11.已知![]() 是方程
是方程![]() 的一个根,
的一个根,![]() _________________.
_________________.
12.在平面直角坐标系中,点(﹣7,m+1)在第三象限,则m的取值范围是_____.
13.已知![]() 、
、![]() 、
、![]() 是反比例函数
是反比例函数![]() 的图象上的三点,且
的图象上的三点,且![]() ,则
,则![]() 、
、![]() 、
、![]() 的大小关系是________________.
的大小关系是________________.
14.点A(-1,y1),B(2,y2)均在直线y=-2x+b的图象上,则y1___________y2(选填“>”<”=”)
15.如图,![]() 的对角线
的对角线![]() ,
,![]() 相交于点
相交于点![]() ,且
,且![]() ,
,![]() ,
,![]() ,则
,则![]() 的面积为______.
的面积为______.
16.已知实数![]() 满足
满足![]() ,则以
,则以![]() 的值为两边长的等腰三角形的周长是_________________.
的值为两边长的等腰三角形的周长是_________________.
三、解下列各题(本大题共8小题,共72分)
17.(8分)列方程解应用题:从甲地到乙地有两条公路,一辆私家车在高速公路上的平均速度比在普通公路上的平均速度高![]() ,行驶
,行驶![]() 千米的高速公路比行驶同等长度的普通公路节约
千米的高速公路比行驶同等长度的普通公路节约![]() 分钟,求该汽车在高速公路上的平均速度.
分钟,求该汽车在高速公路上的平均速度.
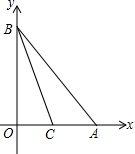
18.(8分)如图,点A和点B分别在x轴和y轴上,且OA=OB=4,直线BC交x轴于点C,S△BOC=S△ABC.
(1)求直线BC的解析式;
(2)在直线BC上求作一点P,使四边形OBAP为平行四边形(尺规作图,保留痕迹,不写作法).
19.(8分)如图,过点A的一次函数的图象与正比例函数y=2x的图象相交于点B.
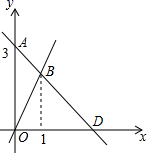
(1)求该一次函数的解析式;
(2)若该一次函数的图象与x轴交于点D,求△BOD的面积.
20.(8分)如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.
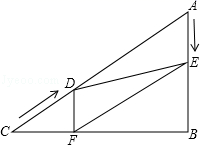
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
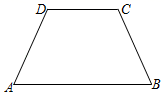
21.(8分)如图,在四边形ABCD中,AB∥DC,边AD与BC不平行
(1)若∠A=∠B,求证:AD=BC.
(2)已知AD=BC,∠A=70°,求∠B的度数.
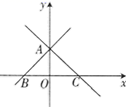
22.(10分)因为一次函数![]() 与
与![]() 的图象关于
的图象关于![]() 轴对称,所以我们定义:函数
轴对称,所以我们定义:函数![]() 与互为
与互为![]() “镜子”函数.
“镜子”函数.
(1)请直接写出函数![]() 的“镜子”函数:________.
的“镜子”函数:________.
(2)如图,一对“镜子”函数![]() 与
与![]() 的图象交于点
的图象交于点![]() ,分别与
,分别与![]() 轴交于
轴交于![]() 两点,且AO=BO,△ABC的面积为
两点,且AO=BO,△ABC的面积为![]() ,求这对“镜子”函数的解析式.
,求这对“镜子”函数的解析式.
23.(10分)如图,将一矩形纸片OABC放在平面直角坐标系中,![]() ,
,![]() ,
,![]() .动点Q从点O出发以每秒1个单位长的速度沿OC向终点C运动,运动
.动点Q从点O出发以每秒1个单位长的速度沿OC向终点C运动,运动![]() 秒时,动点P从点A出发以相同的速度沿AO向终点O运动.当其中一点到达终点时,另一点也停止运动.设点P的运动时间为t(秒).
秒时,动点P从点A出发以相同的速度沿AO向终点O运动.当其中一点到达终点时,另一点也停止运动.设点P的运动时间为t(秒).
(1)OP =____________, OQ =____________;(用含t的代数式表示)
(2)当![]() 时,将△OPQ沿PQ翻折,点O恰好落在CB边上的点D处.
时,将△OPQ沿PQ翻折,点O恰好落在CB边上的点D处.
①求点D的坐标;
②如果直线y = kx + b与直线AD平行,那么当直线y = kx + b与四边形PABD有交点时,求b 的取值范围.
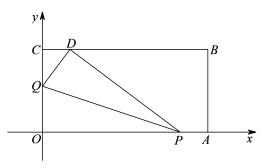
24.(12分)已知y与x+3成正比例,且当x=1时,y=8
(1)求y与x之间的函数关系式;
(2)若点(a,6)在这个函数的图象上,求a的值.
参考答案
一、选择题(每小题3分,共30分)
1、B
2、B
3、D
4、B
5、C
6、D
7、B
8、B
9、C
10、B
二、填空题(本大题共有6小题,每小题3分,共18分)
11、15
12、m<-1
13、y2<y1<y3
14、>.
15、1
16、19
三、解下列各题(本大题共8小题,共72分)
17、![]() .
.
18、(1)![]() ;(2)见解析.
;(2)见解析.
19、(1)y=﹣x+1;(2)△BOD的面积=1.
20、(1)见解析;(2)能,t=10;(3)t=![]() 或12.
或12.
21、 (1)证明见解析;(2)∠B=70°.
22、 (1)y=-3x-2;(2)![]() ;
;![]() .
.
23、(1)6-t; t+![]() (2)①D(1,3) ②3≤b≤
(2)①D(1,3) ②3≤b≤![]()
24、(1)y=1x+6;(1)2.
2023-2024学年黑龙江省大庆市三站中学数学九上期末综合测试模拟试题含答案: 这是一份2023-2024学年黑龙江省大庆市三站中学数学九上期末综合测试模拟试题含答案,共7页。
2023-2024学年黑龙江大庆市三站中学八上数学期末统考试题含答案: 这是一份2023-2024学年黑龙江大庆市三站中学八上数学期末统考试题含答案,共8页。试卷主要包含了考生必须保证答题卡的整洁等内容,欢迎下载使用。
黑龙江省大庆市肇源县三站中学2022-2023学年七年级下学期期末数学试题: 这是一份黑龙江省大庆市肇源县三站中学2022-2023学年七年级下学期期末数学试题,共20页。












