2022-2023学年湖北省省直辖县数学七下期末预测试题含答案

2022-2023学年湖北省省直辖县数学七下期末预测试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项：

1． 答题前，考生先将自己的姓名、准考证号填写清楚，将条形码准确粘贴在考生信息条形码粘贴区。

2．选择题必须使用2B铅笔填涂；非选择题必须使用0．5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚。

3．请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效。

4．保持卡面清洁，不要折叠，不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、选择题(每小题3分,共30分)

1．学校为创建“书香校园”购买了一批图书．已知购买科普类图书花费10000元，购买文学类图书花费9000元，其中科普类图书平均每本的价格比文学类图书平均每本的价格贵5元，且购买科普书的数量比购买文学书的数量少100本．求科普类图书平均每本的价格是多少元？若设科普类图书平均每本的价格是x元，则可列方程为（　　）

A．﹣=100 B．﹣=100

C．﹣=100 D．﹣=100

2．下列各式从左到右是分解因式的是(   )

A．a(x+y)＝ax+ay

B．10x2﹣5x＝5x(2x﹣1)

C．8m3n＝2m3•4n

D．t2﹣16+3t＝(t+4)(t﹣4)+3t

3．如图，在四边形ABCD中，∠A=90°，AB=3，，点M、N分别为线段BC、AB上的动点，点E、F分别为DM、MN的中点，则EF长度的最大值为（　　）

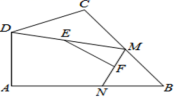
A．2 B．3 C．4 D．

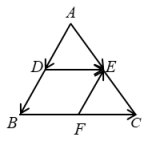
4．如图，已知，点D、E、F分别是、、的中点，下列表示不正确的是（）

A． B． C． D．

5．已知三角形的三边为2、3、4，该三角形的面积为(    )

A． B． C． D．

6．如图，一个四边形花坛ABCD，被两条线段MN, EF分成四个部分，分别种上红、黄、紫、白四种花卉，种植面积依次是S1、S2、S3、S4，若MN∥AB∥DC，EF∥DA∥CB，则有（  ）

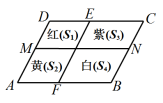
A．S1= S4 B．S1 + S4 = S2 + S3 C．S1 + S3 = S2 + S4 D．S1·S4 = S2·S3

7．某校准备从甲、乙、丙、丁四个科技小组中选出一组，参加区中小学科技创新竞赛，表格记录了各组平时成绩的平均数（单位：分）及方差（单位：分2）：

若要选出一个成绩好且状态稳定的组去参赛，那么应选的组是（    ）

A．甲 B．乙 C．丙 D．丁

8．如果p(2，m)，A（1，1）,B（4，0）三点在同一条直线，那么m的值为（  ）

A．2 B．- C． D．1

9．为了解某市参加中考的25000名学生的身高情况，抽查了其中1200名学生的身高进行统计分析．下列叙述正确的是(　　)

A．25000名学生是总体

B．1200名学生的身高是总体的一个样本

C．每名学生是总体的一个个体

D．以上调查是全面调查

10．计算（    ）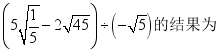

A．7 B．-5 C．5 D．-7

二、填空题(本大题共有6小题，每小题3分，共18分)

11．如图，矩形ABCD的对角线AC与BD交于点0，过点O作BD的垂线分别交AD、BC于E.F两点，若AC =2，∠DAO =300，则FB的长度为________ ．

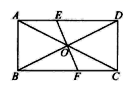
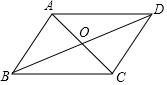
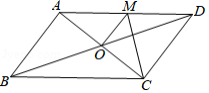
12．如图，在平行四边形ABCD中，AC与BD相交于点O，∠AOB=60°，BD=4，将△ABC沿直线AC翻折后，点B落在点E处，那么S△AED=______

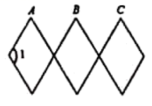
13．如图，是根据四边形的不稳定性制作的边长均为的可活动菱形衣架，若墙上钉子间的距离，则=______度．

14．已知一组数据1,2,0,-1,x,1的平均数是1,则这组数据的极差为____.

15．如图，ABCD的对角线相交于点O，且ADCD，过点O作OMAC，交AD于点M．如果CDM的周长为8，那么ABCD的周长是__．

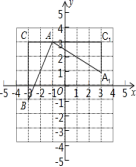
16．如图，在坐标系中，有，且A（﹣1，3），B（﹣3，﹣1），C（﹣3，3），已知是由旋转得到的．请写出旋转中心的坐标是____，旋转角是____度．

三、解下列各题(本大题共8小题，共72分)

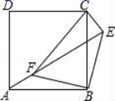
17．（8分）如图，点E是正方形ABCD外一点，点F是线段AE上一点，△EBF是等腰直角三角形，其中∠EBF=90°，连接CE、CF．

（1）求证：△ABF≌△CBE；

（2）判断△CEF的形状，并说明理由．

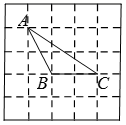
18．（8分）如图，在5×5的网格中，每个格点小正方形的边长为1，△ABC的三个顶点A、B、C都在网格格点的位置上．

（1）请直接写出AB、BC、AC的长度；

（2）求△ABC的面积；

（3）求边AB上的高．

19．（8分）我们给出如下定义：把对角线互相垂直的四边形叫做“正交四边形”.

如图1，在四边形中，，四边形就是“正交四边形”.

（1）下列四边形，一定是“正交四边形”的是______.

①平行四边形②矩形③菱形④正方形

（2）如图2，在“正交四边形”中，点分别是边的中点，求证：四边形是矩形.

（3）小明说：“计算‘正交四边形’的面积可以仿照菱形的方法，面积是对角线之积的一半.”小明的说法正确吗？如果正确，请给出证明；如果错误，请给出反例.

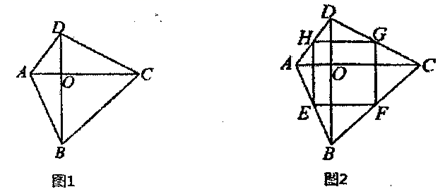
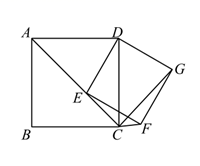
20．（8分）如图，已知四边形ABCD为正方形，点E为线段AC上一点，连接DE，过点E作EF⊥DE，交射线BC于点F，以DE、EF为邻边作矩形DEFG，连接CG．

(1)求证：矩形DEFG是正方形．

(2)当点E从A点运动到C点时；

①求证：∠DCG的大小始终不变；

②若正方形ABCD的边长为2，则点G运动的路径长为         ．

21．（8分）为贯彻党的“绿水青山就是金山银山”的理念，我市计划购买甲、乙两种树苗共7000株用于城市绿化，甲种树苗每株24元，一种树苗每株30元相关资料表明：甲、乙两种树苗的成活率分别为、．

若购买这两种树苗共用去180000元，则甲、乙两种树苗各购买多少株？

若要使这批树苗的总成活率不低于，则甲种树苗至多购买多少株？

在的条件下，应如何选购树苗，使购买树苗的费用最低？并求出最低费用．

22．（10分）新定义：[a，b，c]为二次函数y=ax2+bx+e（a≠0，a，b，c为实数）的“图象数”，如：y=-x2+2x+3的“图象数”为[-1，2，3]

（1）二次函数y=x2-x-1的“图象数”为      ．

（2）若图象数”是[m，m+1，m+1]的二次函数的图象与x轴只有一个交点，求m的值．

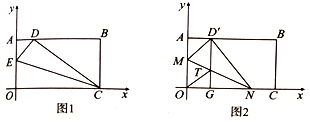
23．（10分）将一矩形纸片放在直角坐标系中，为原点，点在轴上，点在轴上，.

（1）如图1，在上取一点，将沿折叠，使点落在边上的点处，求直线的解析式；

（2）如图2，在边上选取适当的点，将沿折叠，使点落在边上的点处，过作于点，交于点，连接，判断四边形的形状，并说明理由；

（3）、在（2）的条件下，若点坐标，点在直线上，问坐标轴上是否存在点，使以为顶点的四边形是平行四边形，若存在，请直接写出点坐标；若不存在，请说明理由.

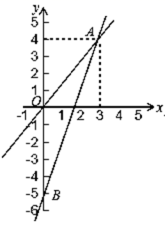
24．（12分）如图，一个正比例函数与一个一次函数的图象交于点A（3，4），其中一次函数与y轴交于B点，且OA＝OB．

（1）求这两个函数的表达式；

（2）求△AOB的面积S．

参考答案

一、选择题(每小题3分,共30分)

1、B

2、B

3、A

4、A

5、D

6、D

7、C

8、C

9、B

10、C

二、填空题(本大题共有6小题，每小题3分，共18分)

11、2

12、

13、1

14、4

15、16

16、    1   

三、解下列各题(本大题共8小题，共72分)

17、（1）证明见解析（2）△CEF是直角三角形

18、（1），，；（2）2；（3）

19、（1）③④ ；（2）详见解析；（3）小明的说法正确.

20、 (1)详见解析;（2）①详见解析;②

21、甲、乙两种树苗各购买5000、2000株；甲种树苗至多购买2800株；最少费用为 元.

22、（1）[，−1，−1]；（2）m1＝−1，m2＝.

23、（1）；（2）四边形为菱形，理由详见解析；（3）以为顶点的四边形是平行四边形时，点坐标或或

24、（1）OA：，AB：；（2）