

2022-2023学年江苏省苏州市园区第十中学数学七年级第二学期期末联考模拟试题含答案
展开2022-2023学年江苏省苏州市园区第十中学数学七年级第二学期期末联考模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项
1.考试结束后,请将本试卷和答题卡一并交回.
2.答题前,请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置.
3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符.
4.作答选择题,必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选涂其他答案.作答非选择题,必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效.
5.如需作图,须用2B铅笔绘、写清楚,线条、符号等须加黑、加粗.
一、选择题(每小题3分,共30分)
1.如图,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为 ( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.正比例函数![]() 的图像上的点到两坐标轴的距离相等,则
的图像上的点到两坐标轴的距离相等,则![]() ( ).
( ).
A.1 B.-1 C.±1 D.±2
3.若代数式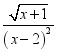 有意义,则实数x的取值范围是( )
有意义,则实数x的取值范围是( )
A.x>1 B.x≠2 C.x≥1且x≠2 D.x≥﹣1且x≠2
4.若不等式组![]() ,只有三个正整数解,则a的取值范围为( )
,只有三个正整数解,则a的取值范围为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.下表记录了甲、乙、丙、丁四名射击运动员最近几次选拔赛成绩的平均数和方差:
| 甲 | 乙 | 丙 | 丁 |
平均数(环) | 9.14 | 9.15 | 9.14 | 9.15 |
方差 | 6.6 | 6.8 | 6.7 | 6.6 |
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应选择( )
A.甲 B.乙 C.丙 D.丁
6.已知一次函数![]() 的图象如图所示,当
的图象如图所示,当![]() 时,
时,![]() 的取值范围是( )
的取值范围是( )
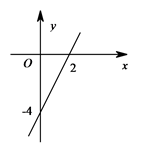
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.如图,阴影部分为一个正方形,此正方形的面积是( )\
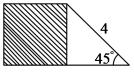
A.2 B.4 C.6 D.8
8.如图,在▱ABCD中,∠BAD=120°,连接BD,作AE∥BD交CD延长线于点E,过点E作EF⊥BC交BC的延长线于点F,且CF=1,则AB的长是( )
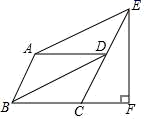
A.2 B.1 C.![]() D.
D.![]()
9.下列四组线段中,不能组成直角三角形的是( )
A.![]() ,
,![]() ,
,![]() B.
B.![]() ,
,![]() ,
,![]()
C.![]() ,
,![]() ,
,![]() D.
D.![]() ,
,![]() ,
,![]()
10.一天李师傅骑车上班途中因车发生故除,修车耽误了一段时间后继续骑行,按时赶到了单位,如图描述了他上班途中的情景,下列说法中错误的是( )
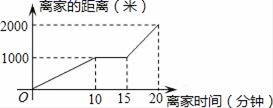
A.李师傅上班处距他家200米
B.李师傅路上耗时20分钟
C.修车后李师傅骑车速度是修车前的2倍
D.李师傅修车用了5分钟
二、填空题(本大题共有6小题,每小题3分,共18分)
11.点A(-1,y1),B(3,y2)是直线y=-4x+3图象上的两点,则y1______y2(填“>”或“<”).
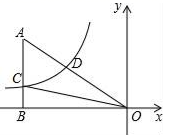
12.已知双曲线![]() 经过Rt△OAB斜边OA的中点D,与直角边AB相交于点C,若S△OAC=3,则k=______.
经过Rt△OAB斜边OA的中点D,与直角边AB相交于点C,若S△OAC=3,则k=______.
13.下表记录了某校4名同学游泳选拨赛成绩的平均数与方差:
| 队员1 | 队员2 | 队员3 | 队员4 |
平均数 | 51 | 50 | 51 | 50 |
方差 | 3.5 | 3.5 | 14.5 | 15.5 |
根据表中数据要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择__________.
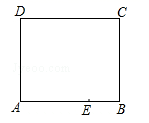
14.如图是一张长方形纸片ABCD,已知AB=8,AD=7,E为AB上一点,AE=5,现要剪下一张等腰三角形纸片(△AEP),使点P落在长方形ABCD的某一条边上,则等腰三角形AEP的底边长是_____________.
15.某一时刻,身高1.6m的小明在阳光下的影长是0.4m,同一时刻同一地点测得旗杆的影长是5m,则该旗杆的高度是_________m.
16. “五一”期间,小红到某景区登山游玩,小红上山时间x(分钟)与走过的路程y(米)之间的函数关系如图所示,在小红出发的同时另一名游客小卉正在距离山底60米处沿相同线路上山,若小红上山过程中与小卉恰好有两次相遇,则小卉上山平均速度v(米/分钟)的取值范围是_____.

三、解下列各题(本大题共8小题,共72分)
17.(8分)如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣1,1),B(﹣3,1),C(﹣1,4).
(1)画出△ABC关于y轴对称的△A1B1C1;
(1)将△ABC绕着点B顺时针旋转90°后得到△A1BC1,请在图中画出△A1BC1.

18.(8分)如图,在△ABC 中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F
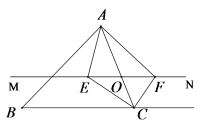
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
19.(8分)某商场计划购进甲、乙两种商品共![]() 件,这两种商品的进价、售价如表所示:
件,这两种商品的进价、售价如表所示:
| 进价(元/件) | 售价(元/件) |
甲种商品 |
|
|
乙种商品 |
|
|
设购进甲种商品![]() (
(![]() ,且
,且![]() 为整数)件,售完此两种商品总利润为
为整数)件,售完此两种商品总利润为![]() 元.
元.
(1)该商场计划最多投入![]() 元用于购进这两种商品共
元用于购进这两种商品共![]() 件,求至少购进甲种商品多少件?
件,求至少购进甲种商品多少件?
(2)求![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)若售完这些商品,商场可获得的最大利润是__________元.
20.(8分)如图,在平面直角坐标系![]() 中,位于第二象限的点
中,位于第二象限的点![]() 在反比例函数
在反比例函数![]() 的图像上,点
的图像上,点![]() 与点
与点![]() 关于原点
关于原点![]() 对称,直线
对称,直线![]() 经过点
经过点![]() ,且与反比例函数
,且与反比例函数![]() 的图像交于点
的图像交于点![]() .
.
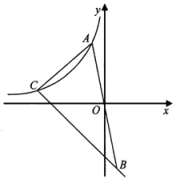
(1)当点![]() 的横坐标是-2,点
的横坐标是-2,点![]() 坐标是
坐标是![]() 时,分别求出
时,分别求出![]() 的函数表达式;
的函数表达式;
(2)若点![]() 的横坐标是点
的横坐标是点![]() 的横坐标的4倍,且
的横坐标的4倍,且![]() 的面积是16,求
的面积是16,求![]() 的值.
的值.
21.(8分)如图,在平面直角坐标系中,矩形OABC的顶点A在y轴的正半轴上,点C在x轴的正半轴上,线段OA,OC的长分别是m,n且满足(m-6)2+![]() =0,点D是线段OC上一点,将△AOD沿直线AD翻折,点O落在矩形对角线AC上的点E处
=0,点D是线段OC上一点,将△AOD沿直线AD翻折,点O落在矩形对角线AC上的点E处
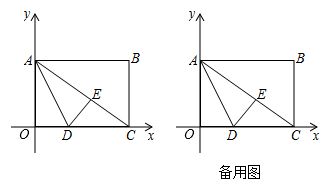
(1)求线段OD的长
(2)求点E的坐标
(3)DE所在直线与AB相交于点M,点N在x轴的正半轴上,以M、A、N、C为顶点的四边形是平行四边形时,求N点坐
22.(10分)一只口袋中放着若干只红球和白球,这两种球除了颜色以外没有任何其他区别,袋中的球已经搅匀,蒙上眼睛从口袋中取出一只球,取出红球的概率是![]() .
.
(1)取出白球的概率是多少?
(2)如果袋中的白球有18只,那么袋中的红球有多少只?
23.(10分)某超市销售一种水果,迸价为每箱40元,规定售价不低于进价.现在的售价为每箱72元,每月可销售60箱.经市场调查发现:若这种牛奶的售价每降低2元,则每月的销量将增加10箱,设每箱水果降价x元(x为偶数),每月的销量为y箱.
(1)写出y与x之间的函数关系式和自变量x的取值范围.
(2)若该超市在销售过程中每月需支出其他费用500元,则如何定价才能使每月销售水果的利润最大?最大利润是多少元?
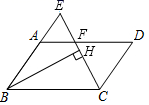
24.(12分)在▱ABCD中,![]() 的平分线与BA的延长线交于点E,CE交AD于F
的平分线与BA的延长线交于点E,CE交AD于F
![]() 求证:
求证:![]() ;
;
![]() 若
若![]() 于点H,
于点H,![]() ,求
,求![]() 的度数.
的度数.
参考答案
一、选择题(每小题3分,共30分)
1、A
2、C
3、D
4、A
5、D
6、C
7、D
8、B
9、A
10、A
二、填空题(本大题共有6小题,每小题3分,共18分)
11、y1>y2
12、﹣1.
13、队员1
14、![]() 或
或![]() 或1
或1
15、20
16、6<v<2或v=4.2
三、解下列各题(本大题共8小题,共72分)
17、 (1)见解析.(1)见解析.
18、 (1)见解析;(2) 当O运动到OA=OC处,四边形AECF是矩形.理由见解析.
19、(1)50件;(2)![]() ;(3)795
;(3)795
20、(1)![]() ,
,![]() ;(2)
;(2)![]() .
.
21、(1)OD=3;(2)E点(![]() ,
,![]() )(3)点N为(
)(3)点N为(![]() ,0)或(
,0)或(![]() ,0)
,0)
22、 (1)![]() (2)袋中的红球有6只.
(2)袋中的红球有6只.
23、(1)y=60+5x,(0≤x≤32,且x为偶数);(2)售价为62元时,每月销售水果的利润最大,最大利润是1920元.
24、![]() 证明见解析
证明见解析![]() 25°
25°
2023-2024学年江苏省苏州市园区第十中学数学九上期末质量检测模拟试题含答案: 这是一份2023-2024学年江苏省苏州市园区第十中学数学九上期末质量检测模拟试题含答案,共9页。试卷主要包含了考生要认真填写考场号和座位序号,一人乘雪橇沿如图所示的斜坡,有一组数据等内容,欢迎下载使用。
江苏省苏州市苏州工业园区2022-2023学年七年级数学第二学期期末监测模拟试题含答案: 这是一份江苏省苏州市苏州工业园区2022-2023学年七年级数学第二学期期末监测模拟试题含答案,共6页。试卷主要包含了答题时请按要求用笔, “已知,函数y=中自变量x的取值范围是等内容,欢迎下载使用。
江苏省苏州市工业园区2022-2023学年数学七年级第二学期期末质量检测模拟试题含答案: 这是一份江苏省苏州市工业园区2022-2023学年数学七年级第二学期期末质量检测模拟试题含答案,共6页。试卷主要包含了答题时请按要求用笔,在平行四边形ABCD中,,,下列图形中,是中心对称图形的是等内容,欢迎下载使用。












