江苏省苏州市苏州工业园区2022-2023学年七年级数学第二学期期末监测模拟试题含答案

江苏省苏州市苏州工业园区2022-2023学年七年级数学第二学期期末监测模拟试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项:

1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内。

2．答题时请按要求用笔。

3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效。

4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。

5．保持卡面清洁，不要折暴、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1． “绿水青山就是金山银山”．某工程队承接了60万平方米的荒山绿化任务，为了迎接雨季的到来，实际工作时每天的工作效率比原计划提高了25%，结果提前30天完成了这一任务．设实际工作时每天绿化的面积为x万平方米，则下面所列方程中正确的是（　　）

A． B．

C． D．

2．若a＞b，则下列式子正确的是（）

A．a﹣4＞b﹣3 B．a＜b C．3+2a＞3+2b D．﹣3a＞﹣3b

3．如图，矩形ABCD中，点E在边AB上，将矩形ABCD沿直线DE折叠，点A恰好落在BC边上的F处，若CD=6，BF=2，则AD的长是（    ）

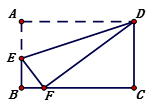
A．7 B．8 C．9 D．10

4．八边形的内角和、外角和共多少度（    ）

A． B． C． D．

5．如果，那么（      ）

A． B． C． D．x为一切实数

6．如图，在四边形中，，分别是的中点，则四边形一定是（    ）

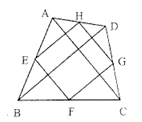
A．平行四边形 B．矩形 C．菱形 D．正方形

7． “已知：正比例函数 与反比例函数 图象相交于 两点， 其横坐标分别是 1 和﹣1，求不等式 的解集．”对于这道题，某同学是这样解答的：“由图象可知：当或 时，，所以不等式的解集是或”．他这种解决问题的思路体现的数学思想方法是(     )

A．数形结合 B．转化 C．类比 D．分类讨论

8．如图，在▱ABCD中，已知AD=12cm，AB=8cm，AE平分∠BAD交BC边于点E，则CE的长等于（ ）

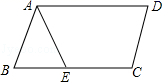
A．8cm B．6cm C．4cm D．2cm

9．函数y=中自变量x的取值范围是（　　）

A．x＞3 B．x＜3 C．x≤3 D．x≥﹣3

10．四边形是平行四边形，下列结论中正确的是（  ）

A．当时，它是菱形 B．当时，它是矩形

C．当时，它是正方形 D．当时，它是正方形

11．矩形、菱形、正方形都具有的性质是（　　）

A．对角线互相垂直

B．对角线互相平分

C．对角线相等

D．每一条对角线平分一组对角

12．某商品的进价为每件40元．当售价为每件60元时，每星期可卖出300件，现需降价处理，为抢占市场份额，且经市场调查：每降价1元，每星期可多卖出20件．现在要使利润为6120元，每件商品应降价（　　）元．

A．3    B．5    C．2    D．2.5

二、填空题（每题4分，满分20分，将答案填在答题纸上）

13．因式分解：          ．

14．一个多边形的内角和是 1440°，则这个多边形是__________边形．

15．如图，正方形ABCD和正方形CEFG中，点D在CG上，BC=1，CE=3，H是AF的中点，那么CH的长是______．

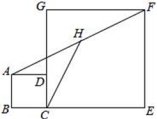
16．已知有两点、都在一次函数的图象上，则的大小关系是______（用“<”连接）

17．一元二次方程的根是_____________

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18．（5分）某超市预测某饮料有发展前途，用1600元购进一批饮料，面市后果然供不应求，又用6000元购进这批饮料，第二批饮料的数量是第一批的3倍，但单价比第一批贵2元.

(1)第一批饮料进货单价多少元？

(2)若二次购进饮料按同一价格销售，两批全部售完后，获利不少于1200元，那么销售单价至少为多少元？

19．（5分）某汽车租凭公司要购买轿车和面包车共辆，其中轿车最少要购买辆，轿车每辆万元，购头面包车每辆万元，公司可投入的购车资金不超过万元．

（1）符合公司要求的购买方案有几种？请说明理由；

（2）如果每辆轿车日租金为元，每辆面包车日租金为元，假设新购买的这辆汽车每日都可以全部租出，公司希望辆汽车的日租金最高，那么应该选择以上的哪种购买方案？且日租金最高为多少元？

20．（8分）某商店的一种服装，每件成本为50元．经市场调研，售价为60元时，可销售800件；售价每提高5元，销售量将减少100件．求每件商品售价是多少元时，商店销售这批服装获利能达到12000元？

21．（10分）阅读材料：解分式不等式＜1

解：根据实数的除法法则：同号两数相除得正数，异号两数相除得负数，因此，原不等式可转化为：

①或②

解①得：无解，解②得：﹣2＜x＜1

所以原不等式的解集是﹣2＜x＜1

请仿照上述方法解下列分式不等式：（1）＞1；（2）＜1．

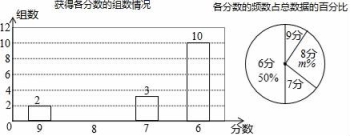
22．（10分）目前由重庆市教育委员会，渝北区人们政府主办的“阳光下成长”重庆市第八届中小学生艺术展演活动落下帷幕，重庆一中学生舞蹈团、管乐团、民乐团、声乐团、话剧团等五大艺术团均荣获艺术表演类节目一等奖，重庆一中获优秀组织奖，重庆一中老师李珊获先进个人奖，其中重庆一中舞蹈团将代表重庆市参加明年的全国集中展演比赛，若以下两个统计图统计了舞蹈组各代表队的得分情况：

（1）m＝　   　，在扇形统计图中分数为7的圆心角度数为　   　度．

（2）补全条形统计图，各组得分的中位数是　   　分，众数是　   　分．

（3）若舞蹈组获得一等奖的队伍有2组，已知主办方各组的奖项个数是按相同比例设置的，若参加该展演活动的总队伍数共有120组，那么该展演活动共产生了多少个一等奖？

23．（12分）二次根式计算：

（1）；

（2）；

（3）（）÷；

（4）．

参考答案

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1、C

2、C

3、D

4、B

5、B

6、B

7、A

8、C

9、B

10、B

11、B

12、A

二、填空题（每题4分，满分20分，将答案填在答题纸上）

13、

14、十

15、

16、

17、，

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18、（1）第一批饮料进货单价为8元.(2) 销售单价至少为11元.

19、（1）三种，理由见解析；（2）购买5辆轿车，5辆面包车时，日租金最高为1550元．

20、70或80

21、 (1) ； (2) 

22、（1）25，54；（2）如图所示见解析；6.5，6；（3）该展演活动共产生了12个一等奖．

23、（1）8；（2）；（3）；（4）1．