2022-2023学年江苏省扬州市枣林湾学校数学七年级第二学期期末监测模拟试题含答案

2022-2023学年江苏省扬州市枣林湾学校数学七年级第二学期期末监测模拟试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

请考生注意：

1．请用2B铅笔将选择题答案涂填在答题纸相应位置上，请用0．5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。

2．答题前，认真阅读答题纸上的《注意事项》，按规定答题。

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1．甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数与方差s2如下表所示：

根据表中数据，要从中选择一名成绩好又发挥稳定的运动员参加比赛，应该选择（　　）

A．甲 B．乙 C．丙 D．丁

2．与是同类二次根式的是（　　）

A． B． C． D．

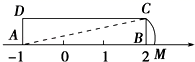
3．点A（m﹣1，n+1）在平面直角坐标系中的位置如图所示，则坐标为（m+1，n﹣1）的点是（　　）

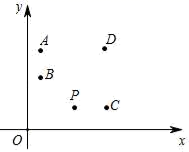
A．P点 B．B点 C．C点 D．D点

4．在同一条道路上，甲车从A地到B地，乙车从B地到A地，乙先出发，图中的折线段表示甲、乙两车之间的距离y（千米）与行驶时间x（小时）的函数关系的图象，下列说法错误的是（　　）

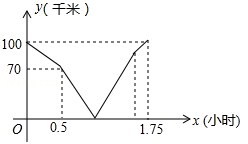
A．乙先出发的时间为0.5小时 B．甲的速度是80千米/小时

C．甲出发0.5小时后两车相遇 D．甲到B地比乙到A地早小时

5．在联欢会上，有A、B、C三名选手站在一个三角形的三个顶点位置上，他们在玩“抢凳子”游戏，要求在他们中间放一个木凳，谁先抢到凳子谁获胜，为使游戏公平，则凳子应放的最适当的位置是在的（    ）

A．三边中垂线的交点 B．三边中线的交点

C．三条角平分线的交点 D．三边上高的交点

6．如图，在梯形ABCD中，AB∥CD，中位线EF与对角线AC、BD交于M、N两点，若EF=18cm，MN=8cm，则AB的长等于（　　）cm

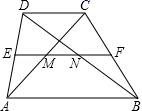
A．10 B．13 C．20 D．26

7．如图，点是正方形的边上一点，把绕点顺时针旋转到的位置．若四边形AECF的面积为20，DE=2，则AE的长为（   ）

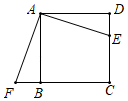
A．4 B． C．6 D．

8．下列二次根式中，属于最简二次根式的是（    ）

A． B．  C． D．

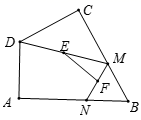
9．如图，在四边形中，，点分别为线段上的动点(含端点，但点不与点重合)，点分别为的中点，则长度的最大值为(  )

A． B． C． D．

10．下列各组数中,以它们为边长的线段不能构成直角三角形的是( )

A．1，，2 B．1，2，

C．5，12，13 D．1，，

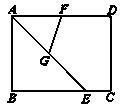
11．已知矩形ABCD如图，AB＝3，BC＝4，AE平分∠BAD交BC于点E，点F、G分别为AD、AE的中点，则FG＝（    ）

A． B． C．2 D．

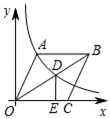
12．如图，在平面直角坐标系中，菱形ABCO的顶点O为坐标原点，边CO在x轴正半轴上，∠AOC＝60°，反比例函数y＝(x＞0)的图象经过点A，交菱形对角线BO于点D，DE⊥x轴于点E，则CE长为(   )

A．1 B． C．2﹣ D．﹣1

二、填空题（每题4分，满分20分，将答案填在答题纸上）

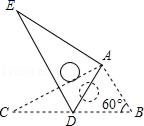
13．如图，将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE，点B的对应点D恰好落在BC边上，若AC＝，∠B＝60°，则CD的长为_____．

14．小王参加某企业招聘测试，笔试、面试、技能操作得分分别为分、分、分，按笔试占、面试占、技能操作占计算成绩，则小王的成绩是__________．

15．在某校“我的中国梦”演讲比赛中，有9名学生参加决赛他们决赛的最终成绩各不相同．其中的一名学生想要知道自己能否进入前5名，不仅要了解自己的成绩，还要了解这9名学生成绩的_____（从“众数、方差、平均数、中位数”中填答案）

16．已知：，则______.

17．如图，矩形中，，，在数轴上，若以点为圆心，对角线的长为半径作弧交数轴的正半轴于，则点的表示的数为_____．

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18．（5分）物美商场于今年年初以每件25元的进价购进一批商品．当商品售价为40元时，一月份销售256件．二、三月该商品十分畅销．销售量持续走高．在售价不变的基础上，三月底的销售量达到400件．设二、三这两个月月平均增长率不变．

（1）求二、三这两个月的月平均增长率；

（2）从四月份起，商场决定采用降价促销的方式回馈顾客，经调查发现，该商品每降价1元，销售量增加5件，当商品降价多少元时，商场获利4250元？

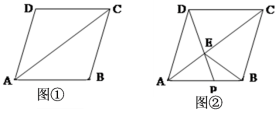
19．（5分）在菱形ABCD中，AC是对角线.

(1)如图①,若AB=6,则菱形ABCD的周长为______；若∠DAB=70º，则∠D的度数是_____；∠DCA的度数是____；

(2)如图②,P是AB上一点,连接DP交对角线AC于点E,连接EB,求证: ∠APD=∠EBC．

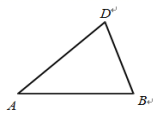
20．（8分）在等腰三角形ABD 中， ABAD．

(I)试利用无刻度的直尺和圆规作图，求作：点C ，使得四边形 ABCD 是菱形.(保留作图痕迹，不写作法和证明)；

(II)在菱形 ABCD 中，连结 AC 交 BD 于点O，若 AC8，BD6，求AB边上的高h的长.

21．（10分）解答题．

某校学生积极为地震灾区捐款奉献爱心．小颖随机抽查其中30名学生的捐款情况如下：（单位：元）2、5、35、8、5、10、15、20、15、5、45、10、2、8、20、30、40、10、15、15、30、15、8、25、25、30、15、8、10、1．

（1）这30名学生捐款的最大值、最小值、极差、平均数各是多少？

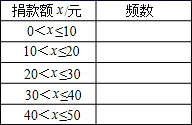
（2）将30名学生捐款额分成下面5组，请你完成频数统计表：

（3）根据上表，作出频数分布直方图．

22．（10分）某校在一次广播操比赛中，初二 （1）班、初二（2）班、初二（3）班的各项得分如下：

（1）填空：根据表中提供的信息，在服装统一方面，三个班得分的平均数是________；在动作整齐方面三个班得分的众数是________；在动作准确方面最有优势的是________班．

（2）如果服装统一、动作整齐、动作准确三个方面的重要性之比为，那么这三个班的排名顺序怎样？为什么？

（3）在（2）的条件下，你对三个班级中排名最靠后的班级有何建议？

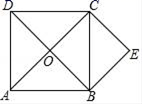
23．（12分）如图，正方形ABCD的对角线AC、BD相交于点O，BE∥AC，CE∥DB．

求证：四边形OBEC是正方形．

参考答案

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1、A

2、B

3、C

4、D

5、A

6、D

7、D

8、C

9、B

10、D

11、D

12、C

二、填空题（每题4分，满分20分，将答案填在答题纸上）

13、1

14、

15、中位数

16、

17、

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18、（1）二、三这两个月的月平均增长率为25%； （2）当商品降价5元时，商品获利4250元．

19、（1）24；110°；35°；（2）见解析.

20、 (I)见解析；(II)

21、 (1) 最大值为1，最小值为2，极差为48，平均数为17.7元．(2)填表见解析；（3）补图见解析.

22、 (1)89分，78分，初二（1）；(2) 排名最好的是初二一班，最差的是初二（2）班，理由见解析；(3)见解析

23、证明见解析