2022-2023学年江苏省扬州市广陵区数学七下期末教学质量检测试题含答案

2022-2023学年江苏省扬州市广陵区数学七下期末教学质量检测试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项：

1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。回答非选择题时，将答案写在答题卡上，写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交回。

一、选择题(每小题3分,共30分)

1．我们八年级下册的数学课本厚度约为0.0085米，用科学记数法表示为（　　）

A．8.5×10﹣4米 B．0.85×10﹣3米 C．8.5×10﹣3米 D．8.5×103米

2．下列各式错误的是（　　）

A． B． C． D．

3．在下列图案中，既是轴对称图形又是中心对称图形的是（  ）

A． B． C． D．

4．如图，在平行四边形中，分别以、为边向外作等边、，延长交于点，点在点、之间，连接，，，则以下四个结论一定正确的是（    ）

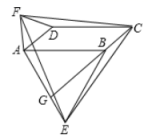
①；②；③④是等边三角形．

A．只有①② B．只有①④ C．只有①②③ D．①②③④

5．如图，ABC中，∠ACB=90°，∠ABC=22.5°，将ABC 绕着点C顺时针旋转，使得点A的对应点D落在边BC上，点B的对应点是点E，连接BE.下列说法中，正确的有（　　）

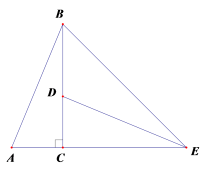
①DE⊥AB     ②∠BCE是旋转角      ③∠BED=30°   ④BDE与CDE面积之比是:1

A．1个 B．2个 C．3个 D．4个

6．在△ABC中，∠C＝90°，AB＝c，∠A＝30°，则AC＝（　　）

A．c B．c C．2c D．c

7．已知点，点都在直线上，则，的大小关系是（     ）

A． B． C． D．无法确定

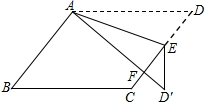
8．如图，在中，为边上一点，将沿折叠至处，与交于点，若，，则的大小为（    ）

A． B． C． D．

9．如果点E、F、G、H分别是四边形ABCD四条边的中点，若EFGH为菱形，则四边形应具备的下列条件中，不正确的个数是（　　）

①一组对边平行而另一组对边不平行； ②对角线互相平分；③对角线互相垂直；④对角线相等

A．1个 B．2个 C．3个 D．4个

10．如图，在△ABC中，AB＝AC，点D在AC上，且BD＝BC＝AD，则∠DBC的度数是（　　　　）

A．36° B．45° C．54° D．72°

二、填空题(本大题共有6小题，每小题3分，共18分)

11．一组数据2，x，4，6，7，已知这组数据的众数是6，那么这组数据的方差是________．

12．甲，乙，丙三位同学近次快速阅读模拟比赛成绩平均分均为分，且甲，乙，丙的方差是，则发挥最稳定的同学是__________．

13．若的整数部分为，小数部分为，则的值是___.

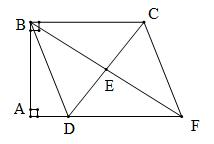
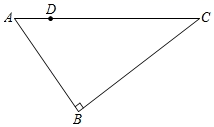
14．如图，四边形ABCD中，,E是边CD的中点，连接BE并延长与AD的延长线相较于点F.若△BCD是等腰三角形，则四边形BDFC的面积为_______________。 

15．与最简二次根式5是同类二次根式，则a=_____．

16．某校女子排球队的15名队员中有4个人是13岁，7个人是14岁，4个人是15岁，则该校女好排球队队员的平均年龄是____岁.

三、解下列各题(本大题共8小题，共72分)

17．（8分）如图，在中，，，，点为边上的一个动点，点从点出发，沿边向运动，当运动到点时停止，设点运动的时间为秒，点运动的速度为每秒1个单位长度．

（1）当时，求的长；

（2）求当为何值时，线段最短？

18．（8分）如图，在正方形ABCD中，AB=3，点E，F分别在CD，AD上，CE=DF，BE，CF相交于点G.

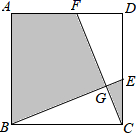
（1）求BGC的度数；

（2）若CE=1，H为BF的中点时，求HG的长度；

（3）若图中阴影部分的面积与正方形ABCD的面积之比为2：3，求△BCG的周长.

19．（8分）如图，中，、两点在对角线上，且.

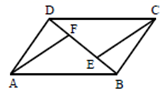
求证：.

20．（8分）某工厂制作甲、乙两种窗户边框，已知同样用12米材料制成甲种边框的个数比制成乙种边框的个数少1个，且制成一个甲种边框比制成一个乙种边框需要多用的材料.

（1）求制作每个甲种边框、乙种边框各用多少米材料？

（2）如果制作甲、乙两种边框的材料共640米，要求制作乙种边框的数量不少于甲种边框数量的2倍，求应最多安排制作甲种边框多少个（不计材料损耗）？

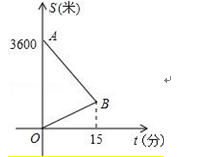
21．（8分）小东到学校参加毕业晚会演出，到学校时发现演出道具还放在家中，此时距毕业晚会开始还有25分钟，于是立即步行回家．同时，他父亲从家里出发骑自行车以他3倍的速度给他送道具，两人在途中相遇，相遇后，小东父亲立即骑自行车以原来的速度载小东返回学校．图中线段AB、OB表示相遇前（含相遇）父亲送道具、小东取道具过程中，各自离学校的路程S（米）与所用时间t分）之间的函数关系，结合图象解答下列问题．

（1）求点B坐标；

（2）求AB直线的解析式；

（3）小东能否在毕业晚会开始前到达学校？

22．（10分）水果批发市场有一种高档水果，如果每千克盈利（毛利润）10元，每天可售出500千克，经市场调查发现，在进货价不变的情况下，若每千克涨价1元，日销量将减少20千克.

（1）若以每千克能盈利18元的单价出售，问每天的总毛利润为多少元？

（2）现市场要保证每天总毛利润6000元，同时又要使顾客得到实惠，则每千克应涨价多少元？

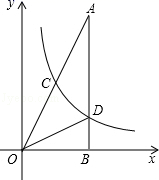
23．（10分）如图，在△AOB中，∠ABO=90°，OB=1，AB=8，反比例函数y=在第一象限内的图象分别交OA，AB于点C和点D，且△BOD的面积S△BOD=1．

（1）求反比例函数解析式；

（2）求点C的坐标．

24．（12分）计算：（1）                  （2）

参考答案

一、选择题(每小题3分,共30分)

1、C

2、A

3、C

4、B

5、C

6、B

7、A

8、B

9、C

10、A

二、填空题(本大题共有6小题，每小题3分，共18分)

11、3.1

12、丙

13、3

14、5或1．

15、1

16、14

三、解下列各题(本大题共8小题，共72分)

17、（1）8；（2）t=．

18、（1）90°；（2）；（3）△BGC的周长为

19、见解析

20、（1）甲框每个2.4米，乙框每个2米；（2）最多可购买甲种边框100个.

21、（1）点B的坐标为（15，900）；（2）s=﹣180t+310；（3）小东能在毕业晚会开始前到达学校．

22、（1）6120元  （2）答应涨价为5元.

23、（1）反比例函数解析式为y=；（2）C点坐标为（2，1）

24、（1）；（2）.