2022-2023学年广西南宁市第四十九中学七年级数学第二学期期末达标检测模拟试题含答案

2022-2023学年广西南宁市第四十九中学七年级数学第二学期期末达标检测模拟试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项：

1． 答题前，考生先将自己的姓名、准考证号填写清楚，将条形码准确粘贴在考生信息条形码粘贴区。

2．选择题必须使用2B铅笔填涂；非选择题必须使用0．5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚。

3．请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效。

4．保持卡面清洁，不要折叠，不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、选择题(每小题3分,共30分)

1．点到轴的距离为（    ）

A．3 B．4 C．5 D．

2．下列分解因式正确的是（　　）

A．x2﹣4＝（x﹣4）（x+4） B．2x3﹣2xy2＝2x（x+y）（x﹣y）

C．x2+y2＝（x+y）2 D．x2﹣2x+1＝x（x﹣2）+1

3．下列图形都是由几个黑色和白色的正方形按一定规律组成，图①中有1个白色正方形，图②中有4个白色正方形，图③中有7个白色正方形，图④中有10个白色正方形，，依次规律，图⑩中白色正方形的个数是(      )

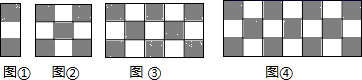
A．27 B．28 C．29 D．30

4．分式 可变形为（   ）

A．       B．  C．             D．

5．一元二次方程x2﹣2x=0的两根分别为x1和x2，则x1x2为（　　）

A．﹣2 B．1 C．2 D．0

6．若反比例函数的图象经过点（﹣1，2），则它的解析式是（　　）

A． B． C． D．

7．如图，在矩形ABCD中，对角线AC，BD交于点O，已知∠AOD＝120°，AB＝2，则矩形的面积为（　　）

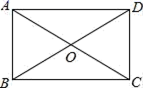
A．2 B．4 C． D．3

8．下列计算过程中，结果是2的是　　

A． B． C． D．

9．如图，直线y=kx+b过A(-1,2),B(-2,0)两点,则0≤kx+b≤-2x的解集为(     )

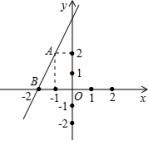
A．x≤-2或x≥-1 B．0≤y≤2 C．-2≤x≤0 D．-2≤x≤-1

10．计算的结果是

A．﹣3 B．3 C．﹣9 D．9

二、填空题(本大题共有6小题，每小题3分，共18分)

11．如图，在一次测绘活动中，某同学站在点A处观测停放于B、C两处的小船，测得船B在点A北偏东75°方向160米处，船C在点A南偏东15°方向120米处，则船B与船C之间的距离为________米．

12．如图，菱形ABCD的对角线相交于点O，AC＝2，BD＝2，将菱形按如图方式折叠，使点B与点O重合，折痕为EF，则五边形AEFCD的周长为_____________

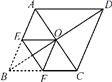
13．如图，函数y＝3x和y＝kx+6的图象相交于点A(a，3)，则不等式3x≤kx+6的解集为_____．

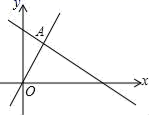
14．如图，直线y＝﹣x+4分别与x轴，y轴相交于点A，B，点C在直线AB上，D是坐标平面内一点，若以点O，A，C，D为顶点的四边形是菱形，则点D的坐标是_____．

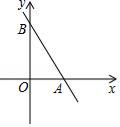
15．如图，正方形ODBC中，OC=1，OA=OB，则数轴上点A表示的数是　　　　．

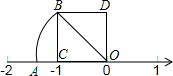
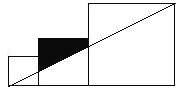
16．将边长分别为2、3、5的三个正方形按图所示的方式排列，则图中阴影部分的面积为　　．

三、解下列各题(本大题共8小题，共72分)

17．（8分）在某校组织的初中数学应用能力竞赛中，每班参加比赛的人数相同，成绩分为A、B、C、D四个等级，其中相应等级的得分依次记为100分、90分、80分、70分，学校将八年级的一班和二班的成绩整理并绘制成如下的统计图，二班D级共有4人．

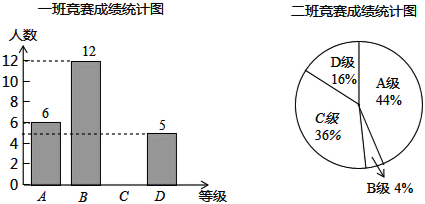
请你根据以上提供的信息解答下列问题：

（1）求此竞赛中一班共有多少人参加比赛，并补全条形统计图．

（2）扇形统计图中A级对应的圆心角度数是　   　．

（3）此次竞赛中二班在C级以上（包括C级）的人数为　   　．

（4）请你将表格补充完成：

18．（8分）如图，矩形的两条边、分别在轴和轴上，已知点 坐标为(4，–3).把矩形沿直线折叠，使点落在点处，直线与、、的交点分别为、、.

(1)线段       ；

(2)求点坐标及折痕的长;

(3)若点在轴上，在平面内是否存在点，使以、、、为顶点的四边形是菱形?若存在，则请求出点的坐标;若不存在，请说明理由;

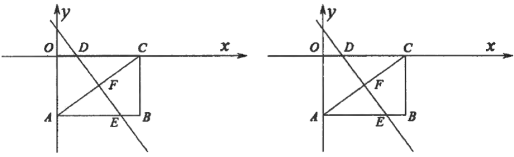
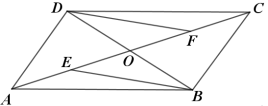
19．（8分）如图，平行四边形ABCD的对角线AC，BD相交于点O，E、F分别是OA、OC的中点．

求证：BE＝DF   

20．（8分）我们把对角线互相垂直的四边形叫做垂美四边形.

(1)（概念理解）在平行四边形、矩形、菱形、正方形中，一定是垂美四边形的是___________.

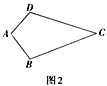
(2)（性质探究）如图2，试探索垂美四边形ABCD的两组对边AB,CD与BC ，AD之间的数量关系，写出证明过程。

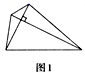
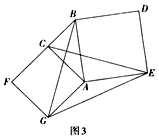
(3)（问题解决）如图3，分别以Rt△ACB的直角边AC和斜边AB为边向外做正方形ACFG和正方形ABDE，连接CE,BG,GE,  已知AC=,BC=1 求GE的长.

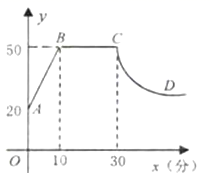
21．（8分）心理学研究发现，一般情况下，在一节45分钟的课中，学生的注意力随学习时间的变化而变化.开始学习时，学生的注意力逐步增强，中间有一段时间学生的注意力保持较为理想的稳定状态，随后学生的注意力开始分散.经过实验分析可知，学生的注意力指标数y随时间x(分钟）的变化规律如下图所示（其中、分别为线段，为双曲线的一部分）。

(1)开始学习后第5分钟时与第35分钟时相比较，何时学生的注意力更集中？

(2)某些数学内容的课堂学习大致可分为三个环节：即“教师引导，回顾旧知——自主探索，合作交流——总结归纳，巩固提高”.其中重点环节“自主探索，合作交流”这一过程一般需要30分钟才能完成，为了确保效果，要求学习时的注意力指标数不低于40，请问这样的课堂学习安排是否合理？并说明理由.

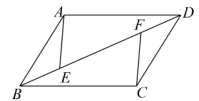
22．（10分）如图，中，，两点在对角线上，．

（1）求证：；

（2）当四边形为矩形时，连结、、，求的值．

23．（10分）甲、乙两家旅行社为了吸引更多的顾客，分别推出赴某地旅游的团体（多于4人）优惠办法．甲旅行社的优惠办法是：买4张全票，其余人按半价优惠；乙旅行社的优惠办法是：所有人都打七五折优惠．已知这两家旅行社的原价均为每人1000元，那么随着团体人数的变化，哪家旅行社的收费更优惠．

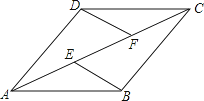
24．（12分）已知：如图，在四边形ABCD中，AB∥CD，E，F为对角线AC上两点，且AE=CF，DF∥BE．

求证：四边形ABCD为平行四边形．

参考答案

一、选择题(每小题3分,共30分)

1、A

2、B

3、B

4、D

5、D

6、B

7、B

8、C

9、D

10、B

二、填空题(本大题共有6小题，每小题3分，共18分)

11、1

12、2

13、x≤1

14、（2，﹣2）或（6，2）

15、

16、

三、解下列各题(本大题共8小题，共72分)

17、（1）25人，见解析；（2）158.4°；（3）21人；（4）见解析.

18、（1）；（2）；拆痕DE的长为； （3）点Q坐标为

19、详见解析

20、菱形、正方形

21、（1）第35分钟时比开始学习后第5分钟学生的注意力更集中；（2）这样的课堂学习安排合理得.

22、（1）证明见解析；（1）1．

23、当团体人数超过8人时，选甲旅行社收费更优惠；当团体人数为8人时，两家旅行社收费相同；当团体人数少于8人时，选乙旅行社收费更优惠．

24、证明见解析.