


2022-2023学年山西省太原五十三中学数学七下期末综合测试试题含答案
展开
这是一份2022-2023学年山西省太原五十三中学数学七下期末综合测试试题含答案,共8页。试卷主要包含了下列各式,关于一次函数,下列结论正确的是,一元二次方程的一次项系数为等内容,欢迎下载使用。
2022-2023学年山西省太原五十三中学数学七下期末综合测试试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 考生须知:1.全卷分选择题和非选择题两部分,全部在答题纸上作答。选择题必须用2B铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。 一、选择题(每小题3分,共30分)1.从﹣3、﹣2、﹣1、1、2、3这六个数中,随机抽取一个数记作a,使关于x的分式方程![]() 有整数解,且使直线y=3x+8a﹣17不经过第二象限,则符合条件的所有a的和是( )A.﹣4 B.﹣1 C.0 D.12.如图,已知直线a∥b∥c,直线m交直线a,b,c于点A,B,C,直线n交直线a,b,c于点D,E,F,若
有整数解,且使直线y=3x+8a﹣17不经过第二象限,则符合条件的所有a的和是( )A.﹣4 B.﹣1 C.0 D.12.如图,已知直线a∥b∥c,直线m交直线a,b,c于点A,B,C,直线n交直线a,b,c于点D,E,F,若![]() ,则
,则![]() 的值为( )
的值为( )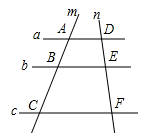 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 3.如果一个正多边形内角和等于1080°,那么这个正多边形的每一个外角等于( )A.
3.如果一个正多边形内角和等于1080°,那么这个正多边形的每一个外角等于( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 4.下列各式:
4.下列各式:![]() 中,是分式的有( )A.1个 B.2个 C.3个 D.4个5.如图,在
中,是分式的有( )A.1个 B.2个 C.3个 D.4个5.如图,在![]() 轴正半轴上依次截取
轴正半轴上依次截取![]() ,过点
,过点![]() 、
、![]() 、
、![]() 、……
、……![]() 分别作
分别作![]() 轴的垂线,与反比例函数
轴的垂线,与反比例函数![]() 交于点
交于点![]() 、
、![]() 、
、![]() 、…、
、…、![]() ,连接
,连接![]() 、
、![]() 、…
、…![]() ,,过点
,,过点![]() 、
、![]() 、…、
、…、![]() 分别向
分别向![]() 、
、![]() 、…、
、…、![]() 作垂线段,构成的一系列直角三角形(图中阴影部分)的面积和等于( ).
作垂线段,构成的一系列直角三角形(图中阴影部分)的面积和等于( ).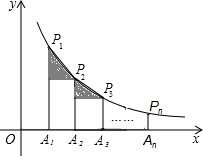 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 6.关于一次函数
6.关于一次函数![]() ,下列结论正确的是
,下列结论正确的是![]()
![]() A.图象经过
A.图象经过![]() B.图象经过第一、二、三象限C.y随x的增大而增大 D.图象与y轴交于点
B.图象经过第一、二、三象限C.y随x的增大而增大 D.图象与y轴交于点![]() 7.一元二次方程
7.一元二次方程![]() 的一次项系数为( )A.1 B.
的一次项系数为( )A.1 B.![]() C.2 D.-28.甲、乙、丙三位选手各10次射击成绩的平均数和方差统计如表:选手甲乙丙平均数9.39.39.3方差0.026a0.032已知乙是成绩最稳定的选手,且乙的10次射击成绩不都一样,则a的值可能是( )A.0 B.0.020 C.0.030 D.0.0359.如图,
C.2 D.-28.甲、乙、丙三位选手各10次射击成绩的平均数和方差统计如表:选手甲乙丙平均数9.39.39.3方差0.026a0.032已知乙是成绩最稳定的选手,且乙的10次射击成绩不都一样,则a的值可能是( )A.0 B.0.020 C.0.030 D.0.0359.如图,![]() ,矩形
,矩形![]() 在
在![]() 的内部,顶点
的内部,顶点![]() ,
,![]() 分别在射线
分别在射线![]() ,
,![]() 上,
上,![]() ,
,![]() ,则点
,则点![]() 到点
到点![]() 的最大距离是( )
的最大距离是( ) 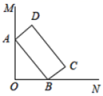 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 10.如图,已知点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是( )
10.如图,已知点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是( )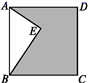 A.48 B.60C.76 D.80二、填空题(本大题共有6小题,每小题3分,共18分)11.一运动员推铅球,铅球经过的路线为如图所示的抛物线,则铅球所经过的路线的函数表达式为________
A.48 B.60C.76 D.80二、填空题(本大题共有6小题,每小题3分,共18分)11.一运动员推铅球,铅球经过的路线为如图所示的抛物线,则铅球所经过的路线的函数表达式为________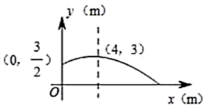 12.若
12.若![]() 是一个完全平方式,则
是一个完全平方式,则![]() ______.13.若将点A(1,3)向左平移2个单位,再向下平移4个单位得到点B, 则点B的坐标为_______.14.如图,已知∠EAD=30°,△ADE绕点A旋转50°后能与△ABC重合,则∠BAE=_________°.
______.13.若将点A(1,3)向左平移2个单位,再向下平移4个单位得到点B, 则点B的坐标为_______.14.如图,已知∠EAD=30°,△ADE绕点A旋转50°后能与△ABC重合,则∠BAE=_________°. 15.若函数y=(m+1)x+(m2-1) (m为常数)是正比例函数,则m的值是____________。16.计算
15.若函数y=(m+1)x+(m2-1) (m为常数)是正比例函数,则m的值是____________。16.计算![]() 的结果等于______________.三、解下列各题(本大题共8小题,共72分)17.(8分)某校为了解八年级男生立定跳远测试情况,随机抽取了部分八年级男生的测试成绩进行统计,根据评分标准,将他们的成绩分为优秀、良好、及格、不及格四个等级,以下是根据调查结果绘制的统计图表的一部分.
的结果等于______________.三、解下列各题(本大题共8小题,共72分)17.(8分)某校为了解八年级男生立定跳远测试情况,随机抽取了部分八年级男生的测试成绩进行统计,根据评分标准,将他们的成绩分为优秀、良好、及格、不及格四个等级,以下是根据调查结果绘制的统计图表的一部分.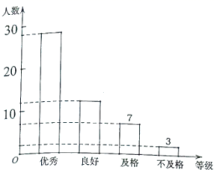
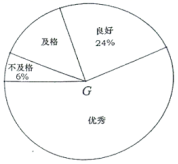 根据以上信息,解答下列问题:(1)被调查的男生中,成绩等级为不及格的男生人数有__________人,成绩等级为良好的男生人数占被调查男生人数的百分比为__________%;(2)被调查男生的总数为__________人,条形统计图中优秀的男生人数为__________人;(3)若该校八年级共有300名男生,根据调查结果,估计该校八年级男生立定跳远测试成绩为良好和优秀的男生人数. 18.(8分)如图,在
根据以上信息,解答下列问题:(1)被调查的男生中,成绩等级为不及格的男生人数有__________人,成绩等级为良好的男生人数占被调查男生人数的百分比为__________%;(2)被调查男生的总数为__________人,条形统计图中优秀的男生人数为__________人;(3)若该校八年级共有300名男生,根据调查结果,估计该校八年级男生立定跳远测试成绩为良好和优秀的男生人数. 18.(8分)如图,在![]() 中,
中,![]() ,
,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,延长
的中点,延长![]() 到
到![]() ,使得
,使得![]() ,连接
,连接![]() 、
、![]() .
.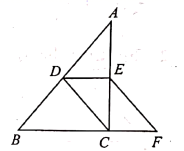 (1)求证:四边形
(1)求证:四边形![]() 为平行四边形;(2)若四边形
为平行四边形;(2)若四边形![]() 的周长是32,
的周长是32,![]() ,求
,求![]() 的面积;(3)在(2)的条件下,求点
的面积;(3)在(2)的条件下,求点![]() 到直线
到直线![]() 的距离. 19.(8分)在四个互不相等的正整数中,最大的数是8,中位数是4,求这四个数(按从小到大的顺序排列) 20.(8分)如图,点C为AD的中点,过点C的线段BE⊥AD,且AB=DE.求证:AB∥ED.
的距离. 19.(8分)在四个互不相等的正整数中,最大的数是8,中位数是4,求这四个数(按从小到大的顺序排列) 20.(8分)如图,点C为AD的中点,过点C的线段BE⊥AD,且AB=DE.求证:AB∥ED.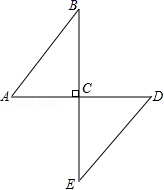 21.(8分)在平面直角坐标系xOy中,对于与坐标轴不平行的直线l和点P,给出如下定义:过点P作x轴,y轴的垂线,分别交直线l于点M,N,若PM+PN≤4,则称P为直线l的近距点,特别地,直线上l所有的点都是直线l的近距点.已知点A(-
21.(8分)在平面直角坐标系xOy中,对于与坐标轴不平行的直线l和点P,给出如下定义:过点P作x轴,y轴的垂线,分别交直线l于点M,N,若PM+PN≤4,则称P为直线l的近距点,特别地,直线上l所有的点都是直线l的近距点.已知点A(-![]() ,0),B(0,2),C(-2,2).(1)当直线l的表达式为y=x时,①在点A,B,C中,直线l的近距点是 ;②若以OA为边的矩形OAEF上所有的点都是直线l的近距点,求点E的纵坐标n的取值范围;(2)当直线l的表达式为y=kx时,若点C是直线l的近距点,直接写出k的取值范围.
,0),B(0,2),C(-2,2).(1)当直线l的表达式为y=x时,①在点A,B,C中,直线l的近距点是 ;②若以OA为边的矩形OAEF上所有的点都是直线l的近距点,求点E的纵坐标n的取值范围;(2)当直线l的表达式为y=kx时,若点C是直线l的近距点,直接写出k的取值范围. 22.(10分)一个有进水管与出水管的容器,从某时刻开始的3分内只进水不出水,在随后的9分内既进水又出水,每分的进水量和出水量都是常数.容器内的水量y(单位:升)与时间x(单位:分)之间的关系如图所示.①当0≤x≤3时,求y与x之间的函数关系.②3<x≤12时,求y与x之间的函数关系.③当容器内的水量大于5升时,求时间x的取值范围.
22.(10分)一个有进水管与出水管的容器,从某时刻开始的3分内只进水不出水,在随后的9分内既进水又出水,每分的进水量和出水量都是常数.容器内的水量y(单位:升)与时间x(单位:分)之间的关系如图所示.①当0≤x≤3时,求y与x之间的函数关系.②3<x≤12时,求y与x之间的函数关系.③当容器内的水量大于5升时,求时间x的取值范围.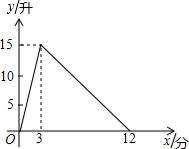 23.(10分)图(a)、图(b)、图(c)是三张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1.请在图(a)、图(b)、图(c)中,分别画出符合要求(1),(2),(3)的图形,所画图形各顶点必须与方格纸中的小正方形顶点重合.
23.(10分)图(a)、图(b)、图(c)是三张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1.请在图(a)、图(b)、图(c)中,分别画出符合要求(1),(2),(3)的图形,所画图形各顶点必须与方格纸中的小正方形顶点重合.

 (1)画一个底边为4,面积为8的等腰三角形;(2)画一个面积为10的等腰直角三角形;(3)画一个面积为12的平行四边形。 24.(12分)在初中阶段的函数学习中,我们经历了“确定函数的表达式——利用函数图象研究其性质一一运用函数解决问题”的学习过程.在画函数图象时,我们通过描点或平移的方法画出了所学的函数图象.同时,我们也学习了绝对值的意义
(1)画一个底边为4,面积为8的等腰三角形;(2)画一个面积为10的等腰直角三角形;(3)画一个面积为12的平行四边形。 24.(12分)在初中阶段的函数学习中,我们经历了“确定函数的表达式——利用函数图象研究其性质一一运用函数解决问题”的学习过程.在画函数图象时,我们通过描点或平移的方法画出了所学的函数图象.同时,我们也学习了绝对值的意义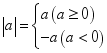 .结合上面经历的学习过程,现在来解决下面的问题:在函数
.结合上面经历的学习过程,现在来解决下面的问题:在函数![]() 中,当
中,当![]() 时,
时,![]() 当
当![]() 时,
时,![]() .
.![]() 求这个函数的表达式;
求这个函数的表达式;![]() 在给出的平面直角坐标系中,请用你喜欢的方法画出这个函数的图象;
在给出的平面直角坐标系中,请用你喜欢的方法画出这个函数的图象;![]() 已知函数
已知函数![]() 的图象如图所示,结合你所画的函数图象,直接写出不等式
的图象如图所示,结合你所画的函数图象,直接写出不等式![]() 的解集.
的解集.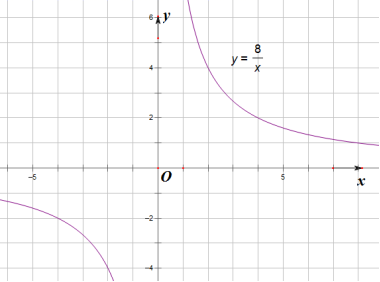 参考答案 一、选择题(每小题3分,共30分)1、B2、A3、A4、D5、B6、D7、D8、B9、B10、C 二、填空题(本大题共有6小题,每小题3分,共18分)11、
参考答案 一、选择题(每小题3分,共30分)1、B2、A3、A4、D5、B6、D7、D8、B9、B10、C 二、填空题(本大题共有6小题,每小题3分,共18分)11、![]() 12、
12、![]() 13、(﹣1,﹣1)14、2015、216、
13、(﹣1,﹣1)14、2015、216、![]() 三、解下列各题(本大题共8小题,共72分)17、(1)3,24;(2)50,28;(3)估计该校八年级男生立定跳远测试成绩在良好以上的男生人数为240人.18、(1)见解析;(2)96;(3)4.819、这四个数为
三、解下列各题(本大题共8小题,共72分)17、(1)3,24;(2)50,28;(3)估计该校八年级男生立定跳远测试成绩在良好以上的男生人数为240人.18、(1)见解析;(2)96;(3)4.819、这四个数为![]() 或
或![]() 或
或![]() .20、详见解析21、(1)①A,B;②n的取值范围是
.20、详见解析21、(1)①A,B;②n的取值范围是![]() ,且
,且![]() ;(2)
;(2) ![]() .22、①当0≤x≤3时,y与x之间的函数关系式为y=5x;②
.22、①当0≤x≤3时,y与x之间的函数关系式为y=5x;②![]() ;③1<x<1.23、如图所示:
;③1<x<1.23、如图所示: 24、
24、![]()
![]() ;
; ![]() 详见解析;
详见解析;![]()
![]() 或
或![]()
相关试卷
这是一份山西省太原市第五十三中学2023-2024学年九年级数学第一学期期末综合测试模拟试题含答案,共7页。试卷主要包含了考生要认真填写考场号和座位序号,如图,是的直径,是弦,点是劣弧,抛物线的对称轴是等内容,欢迎下载使用。
这是一份2023-2024学年山西省太原市育英中学数学八上期末经典试题含答案,共7页。
这是一份2023-2024学年山西省太原志达中学数学八上期末达标测试试题含答案,共8页。试卷主要包含了下列命题中,是假命题的是等内容,欢迎下载使用。








