2022-2023学年山东省青州市七年级数学第二学期期末统考模拟试题含答案

2022-2023学年山东省青州市七年级数学第二学期期末统考模拟试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项：

1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。回答非选择题时，将答案写在答题卡上，写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交回。

一、选择题(每小题3分,共30分)

1．若点P(1－m，-3)在第三象限，则m的取值范围是(    )

A．m<1 B．m<0 C．m>0 D．m>1

2．如图，在平面直角坐标系中有两点A（5，0），B（0，4），则它们之间的距离为（　　）

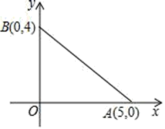
A． B． C． D．

3．如图，点A坐标为（3，0），B是y轴正半轴上一点，AB=5，则点B的坐标为（　　）

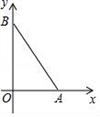
A．（4，0） B．（0，4） C．（0，5） D．（0，）

4．如果ab＞0，a＋b＜0，那么下面各式：①  ；  ②＝1；③＝－b．其中正确的是(   )

A．①② B．①③ C．①②③ D．②③

5．下列事件：①上海明天是晴天，②铅球浮在水面上，③平面中，多边形的外角和都等于360度，属于确定事件的个数有（　　）

A．0个 B．1个 C．2个 D．3个

6．中国传统扇文化有着深厚的底蕴，下列扇面图形是中心对称图形的是(    )

A． B． C． D．

7．如图，将矩形ABCD绕点A旋转至矩形AB′C′D′位置，此时AC的中点恰好与D点重合，AB′交CD于点E,若AB=3，则△AEC的面积为（  ）

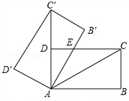
A．3 B．1.5 C．2 D．

8．如图，在菱形ABCD中，∠A＝110°，E，F分别是边AB和BC的中点，EP⊥CD于点P，则∠FPC＝（　　）

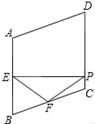
A．35° B．45° C．50° D．55°

9．下列计算正确的是（　　）

A．×=4 B．+= C．÷=2 D．=﹣15

10． “已知：正比例函数 与反比例函数 图象相交于 两点， 其横坐标分别是 1 和﹣1，求不等式 的解集．”对于这道题，某同学是这样解答的：“由图象可知：当或 时，，所以不等式的解集是或”．他这种解决问题的思路体现的数学思想方法是(     )

A．数形结合 B．转化 C．类比 D．分类讨论

二、填空题(本大题共有6小题，每小题3分，共18分)

11．如图，在中，，D是AB的中点，若，则的度数为________。

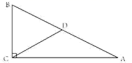
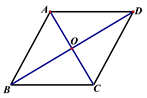
12．如图，在ABCD中，对角线AC，BD相交于点O，若再增加一个条件，就可得出ABCD是菱形，则你添加的条件是___________．

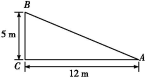
13．如图，一根旗杆在离地面5 m处断裂，旗杆顶部落在离旗杆底部12 m处，旗杆断裂之前的高为____. 

14．若整数m满足，且，则m的值为___________.

15．点A（a,b）是一次函数y=x+2与反比例函数的图像的交点，则__________。

16．如图，在矩形ABCD中，AB＝5，AD＝9，点P为AD边上点，沿BP折叠△ABP，点A的对应点为E，若点E到矩形两条较长边的距离之比为1：4，则AP的长为_____．

三、解下列各题(本大题共8小题，共72分)

17．（8分）在学习了正方形后，数学小组的同学对正方形进行了探究，发现：

（1）如图1，在正方形ABCD中，点E为BC边上任意一点（点E不与B、C重合），点F在线段AE上，过点F的直线MN⊥AE，分别交AB、CD于点M、N . 此时，有结论AE=MN，请进行证明；

（2）如图2：当点F为AE中点时，其他条件不变，连接正方形的对角线BD， MN 与BD交于点G，连接BF，此时有结论：BF= FG，请利用图2做出证明.

（3）如图3：当点E为直线BC上的动点时，如果（2）中的其他条件不变，直线MN分别交直线AB、CD于点M、N，请你直接写出线段AE与MN之间的数量关系、线段BF与FG之间的数量关系.

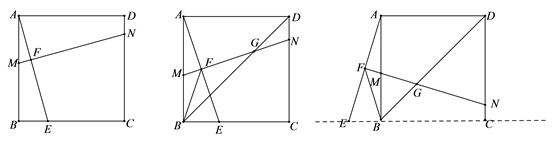
       图1                      图2                        图3

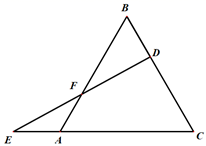
18．（8分）如图，点在等边三角形的边，延长至，使，连接交于.

求证：.

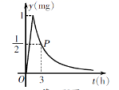
19．（8分）为了预防流感，某学校在休息日用药熏消毒法对教室进行消毒. 已知药物释放过程中，室内每立方米空气中的含药量y（mg）与时间t（h）成正比；药物释放完毕后，y与t之间的函数解析式为y=（a为常数），如图所示. 根据图中提供的信息，解答下列问题：

（1）写出从释放药物开始，y与t之间的两个函数解析式及相应的自变量取值范围；

（2）据测定，当空气中每立方米的含药量降低到0.25mg以下时，学生方可进入教室，那么药物释放开始，至少需要经过多少小时，学生才能进入教室？

20．（8分）在平面直角坐标系xOy 中，直线与x轴交于点A，与过点B（0，2）且平行于x轴的直线l交于点C，点A关于直线l的对称点为点D．

（1）求点C、D的坐标；

（2）将直线在直线l上方的部分和线段CD记为一个新的图象G．若直线与图象G有两个公共点，结合函数图象，求b的取值范围．

21．（8分）某村为绿化村道，计划在村道两旁种植 A、B 两种树木，需要购买这两种树苗 800 棵，A、B 两种树苗的相关信息如表：

设购买 A 种树苗 x 棵，绿化村道的总费用为 y 元，解答下列问题：

（1）求出 y 与 x 之间的函数关系式．

（2）若这批树苗种植后成活了 670 棵，则绿化村道的总费用需要多少元？

（3）若绿化村道的总费用不超过 120000 元，则最多可购买 B 种树苗多少棵？

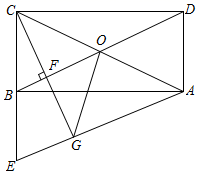
22．（10分）如图，在矩形ABCD中，AC、BD相交于点O，过点A作BD的平行线AE交CB的延长线于点E．

（1）求证：BE＝BC；

（2）过点C作CF⊥BD于点F，并延长CF交AE于点G，连接OG．若BF＝3，CF＝6，求四边形BOGE的周长．

23．（10分）探索发现：，，，根据你发现的规律，回答下列问题：

（1）       ，        ；

（2）利用你发现的规律计算：；

（3）灵活利用规律解方程：.

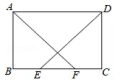
24．（12分）（1）计算：

（2）如图，E、F是矩形ABCD边BC上的两点，且AF=DE．求证：BE=CF．

参考答案

一、选择题(每小题3分,共30分)

1、D

2、A

3、B

4、D

5、C

6、C

7、D

8、D

9、C

10、A

二、填空题(本大题共有6小题，每小题3分，共18分)

11、52

12、AB=BC或BC=CD或CD=AD或AD=AB或AC⊥BD或AB=BC=CD=DA

13、18m

14、，，．

15、-8

16、

三、解下列各题(本大题共8小题，共72分)

17、（1）证明见解析；

（2）证明见解析；

（3）AE与 MN的数量关系是：AE= MN ，BF与FG的数量关系是： BF= FG

18、证明见解析.

19、 (1)y＝t（0≤t≤） (2)6小时

20、（1）D；（2）

21、（1）y＝—50x＋136000；（2）111000 元.（3）若绿化村道的总费用不超过 120000 元，则最多可购买 B 种树苗 1 棵.

22、（1）详见解析；（2）3+1．

23、（1） ，；（2）；（3）.

24、（1）1；（2）见解析