


2022-2023学年山东蒙阴县数学七下期末质量检测模拟试题含答案
展开这是一份2022-2023学年山东蒙阴县数学七下期末质量检测模拟试题含答案,共7页。试卷主要包含了考生要认真填写考场号和座位序号,如果,那么,一元二次方程x2-9=0的解为,下列说法正确的是等内容,欢迎下载使用。
2022-2023学年山东蒙阴县数学七下期末质量检测模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项
1.考生要认真填写考场号和座位序号。
2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。
3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.若![]() ,则
,则![]() ( )
( )
A.7 B.-7 C.5 D.-5
2.下列函数中为正比例函数的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.已知四边形ABCD中,AB∥CD,对角线AC与BD交于点O,下列条件中不能用作判定该四边形是平行四边形条件的是( )
A.AB=CD B.AC=BD C.AD∥BC D.OA=OC
4.(2011•潼南县)目前,全球淡水资源日益减少,提倡全社会节约用水.据测试:拧不紧的水龙头每分钟滴出100滴水,每滴水约0.05毫升.小康同学洗手后,没有把水龙头拧紧,水龙头以测试的速度滴水,当小康离开x分钟后,水龙头滴出y毫升的水,请写出y与x之间的函数关系式是( )
A、y=0.05x B、y=5x
C、y=100x D、y=0.05x+100
5.如果![]() ,那么( )
,那么( )
A.a≥﹣2 B.﹣2≤a≤3
C.a≥3 D.a为一切实数
6.如图,已知△ ABC中,AB=AC,∠ BAC=90°,直角∠ EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,给出以下四个结论:①AE=CF;②△ EPF是等腰直角三角形; ③2S四边形AEPF=S△ ABC; ④BE+CF=EF.当∠ EPF在△ ABC内绕顶点P旋转时(点E与A、B重合).上述结论中始终正确的有( )
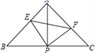
A.1个 B.2个 C.3个 D.4个
7.如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )
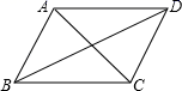
A.当AB=BC时,四边形ABCD是菱形
B.当AC⊥BD时,四边形ABCD是菱形
C.当∠ABC=90°时,四边形ABCD是矩形
D.当AC=BD时,四边形ABCD是正方形
8.下列调查中,适宜采用普查方式的是( )
A.调查一批新型节能灯泡的使用寿命
B.调查常熟市中小学生的课外阅读时间
C.对全市中学生观看电影《厉害了,我的国》情况的调查
D.对卫星“张衡一号”的零部件质量情况的调查
9.一元二次方程x2-9=0的解为( )
A.x1=x2=3 B.x1=x2=-3 C.x1=3,x2=-3 D.x1=![]() ,x2=-
,x2=-![]()
10.下列说法正确的是( )
A.一个游戏中奖的概率是![]() ,则做100次这样的游戏一定会中奖
,则做100次这样的游戏一定会中奖
B.为了了解全国中学生的心理健康状况,应采用普查的方式
C.一组数据0,1,2,1,1的众数和中位数都是1
D.若甲组数据的方差为![]() ,乙组数据的方差为
,乙组数据的方差为![]() ,则乙组数据比甲组数据稳定
,则乙组数据比甲组数据稳定
11.将直线![]() 沿
沿![]() 轴向下平移1个单位长度后得到的直线解析式为( )
轴向下平移1个单位长度后得到的直线解析式为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.一次函数y=kx-k(k<0)的图象大致是( )
A.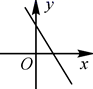 B.
B.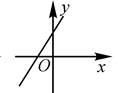 C.
C.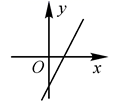 D.
D.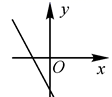
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13.将直线![]() 的图象向上平移3个单位长度,得到直线______.
的图象向上平移3个单位长度,得到直线______.
14. “两直线平行,内错角相等”的逆命题是__________.
15.在4个不透明的袋子中分别装有10个球,其中,1号袋中有10个红球,2号袋中有8个红球.2个白球,3号袋中有5个红球.5个白球,4号袋中有2个红球,8个白球.从各个袋子中任意摸出1个球,摸到白球的可能性最大的是_____(填袋子号).
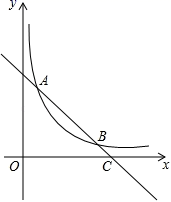
16.如图,直线AB与反比例函数![]() 的图象交于点A(u,p)和点B(v,q),与x轴交于点C,已知∠ACO=45°,若
的图象交于点A(u,p)和点B(v,q),与x轴交于点C,已知∠ACO=45°,若![]() <u<2,则v的取值范围是__________.
<u<2,则v的取值范围是__________.
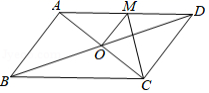
17.如图,![]() ABCD的对角线相交于点O,且AD
ABCD的对角线相交于点O,且AD![]() CD,过点O作OM
CD,过点O作OM![]() AC,交AD于点M.如果
AC,交AD于点M.如果![]() CDM的周长为8,那么
CDM的周长为8,那么![]() ABCD的周长是__.
ABCD的周长是__.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
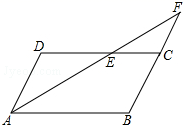
18.(5分)如图,平行四边形ABCD中,![]() ,
,![]() ,AE平分
,AE平分![]() 交BC的延长线于F点,求CF的长.
交BC的延长线于F点,求CF的长.
19.(5分)已知x=2+![]() ,求代数式
,求代数式![]() 的值.
的值.
20.(8分)平面直角坐标系xOy中,对于点M和图形W,若图形W上存在一点N(点M,N可以重合),使得点M与点N关于一条经过原点的直线l对称,则称点M与图形W是“中心轴对称”的
对于图形![]() 和图形
和图形![]() ,若图形
,若图形![]() 和图形
和图形![]() 分别存在点M和点N(点M,N可以重合),使得点M与点N关于一条经过原点的直线l对称,则称图形
分别存在点M和点N(点M,N可以重合),使得点M与点N关于一条经过原点的直线l对称,则称图形![]() 和图形
和图形![]() 是“中心轴对称”的.
是“中心轴对称”的.
特别地,对于点M和点N,若存在一条经过原点的直线l,使得点M与点N关于直线l对称,则称点M和点N是“中心轴对称”的.
(1)如图1,在正方形ABCD中,点![]() ,点
,点![]() ,
,
①下列四个点![]() ,
,![]() ,
,![]() ,
,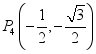 中,与点A是“中心轴对称”的是________;
中,与点A是“中心轴对称”的是________;
②点E在射线OB上,若点E与正方形ABCD是“中心轴对称”的,求点E的横坐标![]() 的取值范围;
的取值范围;
(2)四边形GHJK的四个顶点的坐标分别为![]() ,
,![]() ,
,![]() ,
,![]() ,一次函数
,一次函数![]() 图象与x轴交于点M,与y轴交于点N,若线段与四边形GHJK是“中心轴对称”的,直接写出b的取值范围.
图象与x轴交于点M,与y轴交于点N,若线段与四边形GHJK是“中心轴对称”的,直接写出b的取值范围.
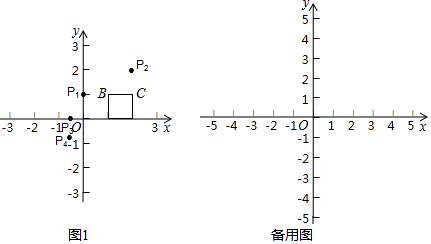
21.(10分)如图,四边形ABCD中,AC⊥BD交BD于点E,点F、M分别是AB、BC的中点,BN平分∠ABE交AM于点N,AB=AC=BD,连接MF,NF
求证:(1)BN=![]() MN;
MN;
(2)△MFN∽△BDC.
22.(10分)已知三角形纸片ABC,其中∠C=90°,AB=10,BC=6,点E,F分别是AC,AB上的点,连接EF.
(1)如图1,若将纸片ABC沿EF折叠,折叠后点A刚好落在AB边上点D处,且S△ADE=S四边形BCED,求ED的长;
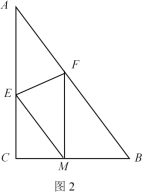
(2)如图2,若将纸片ABC沿EF折叠,折叠后点A刚好落在BC边上点M处,且EM∥AB.
①试判断四边形AEMF的形状,并说明理由;
②求折痕EF的长.

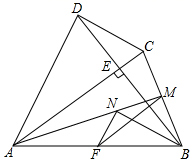
23.(12分)如图,已知点![]() ,
,![]() 分别是平行四边形
分别是平行四边形![]() 的边
的边![]() ,
,![]() 上的中点,且∠
上的中点,且∠![]() =90°.
=90°.
(1)求证:四边形![]() 是菱形;
是菱形;
(2)若![]() =4,
=4,![]() =5,求菱形
=5,求菱形![]() 的面积.
的面积.

参考答案
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、D
2、C
3、B
4、:解:y=100×0.05x,
即y=5x.
故选B.
5、C
6、C
7、D
8、D
9、C
10、C
11、A
12、A
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13、![]()
14、内错角相等,两直线平行
15、1
16、2<v<1
17、16
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18、![]() .
.
19、![]()
20、(1)①P1,P1;②![]() ≤xE≤
≤xE≤![]() ;(2)2
;(2)2![]() ≤b≤2+2
≤b≤2+2![]() 或-2-2
或-2-2![]() ≤b≤-2
≤b≤-2![]() .
.
21、(1)见解析;(2)见解析
22、(1)DE=1;(2)①四边形AEMF是菱形,证明见解析;②![]()
23、(1)见解析;(2)10.
相关试卷
这是一份山东省邹平县2022-2023学年七下数学期末质量检测模拟试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,计算的结果是,已知,下列定理中,没有逆定理的是等内容,欢迎下载使用。
这是一份山东省蒙阴县2022-2023学年七下数学期末复习检测模拟试题含答案,共7页。试卷主要包含了下列调查方法合适的是等内容,欢迎下载使用。
这是一份山东省莒县2022-2023学年七下数学期末教学质量检测模拟试题含答案,共6页。试卷主要包含了答题时请按要求用笔,平行四边形所具有的性质是等内容,欢迎下载使用。












