


2022-2023学年山东省武城县联考七年级数学第二学期期末质量检测试题含答案
展开
这是一份2022-2023学年山东省武城县联考七年级数学第二学期期末质量检测试题含答案,共7页。试卷主要包含了计算的结果是,用反证法证明等内容,欢迎下载使用。
2022-2023学年山东省武城县联考七年级数学第二学期期末质量检测试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 请考生注意:1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.如图,在平行四边形ABCD中,CE⊥AB,E为垂足.如果∠A=115°,则∠BCE=( )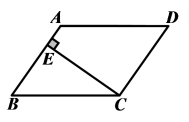 A.25° B.30° C.35° D.55°2.如图,要测量被池塘隔开的A、C两点间的距离,李师傅在AC外任选一点B,连接BA和BC,分别取BA和BC的中点E、F,量得EF两点间距离等于23米,则A、C两点间的距离为()米
A.25° B.30° C.35° D.55°2.如图,要测量被池塘隔开的A、C两点间的距离,李师傅在AC外任选一点B,连接BA和BC,分别取BA和BC的中点E、F,量得EF两点间距离等于23米,则A、C两点间的距离为()米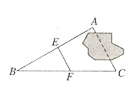 A.23 B.46 C.50 D.23.计算
A.23 B.46 C.50 D.23.计算![]() 的结果是( )A.2 B.
的结果是( )A.2 B.![]() C.
C.![]() D.-24.若平行四边形中两个内角的度数比为1:2,则其中较小的内角是( )。A.60° B.90° C.120° D.45°5.用反证法证明:“若整数系数一元二次方程ax2+bx+c=0(a≠0)有有理根,则a,b,c中至少有一个是偶数”,下列假设中正确的是( )A.假设a,b,c都是偶数
D.-24.若平行四边形中两个内角的度数比为1:2,则其中较小的内角是( )。A.60° B.90° C.120° D.45°5.用反证法证明:“若整数系数一元二次方程ax2+bx+c=0(a≠0)有有理根,则a,b,c中至少有一个是偶数”,下列假设中正确的是( )A.假设a,b,c都是偶数 ![]() B.假设a,b,c都不是偶数C.假设a,b,c至多有一个是偶数
B.假设a,b,c都不是偶数C.假设a,b,c至多有一个是偶数 ![]() D.假设a,b,c至多有两个是偶数6.如图,在菱形
D.假设a,b,c至多有两个是偶数6.如图,在菱形![]() 中,
中,![]() ,
,![]() 的垂直平分线交对角线
的垂直平分线交对角线![]() 于点
于点![]() ,
,![]() 为垂足,连结
为垂足,连结![]() ,则
,则![]() 等于( )
等于( )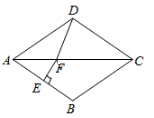 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 7.如图,
7.如图,![]() 中,
中,![]() ,
,![]() 平分
平分![]() ,点
,点![]() 为
为![]() 的中点,连接
的中点,连接![]() ,若
,若![]() 的周长为24,则
的周长为24,则![]() 的长为( )
的长为( )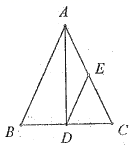 A.18 B.14 C.12 D.68.设a=
A.18 B.14 C.12 D.68.设a= ![]() ,b=
,b= ![]() ,c=
,c=![]() ,则a,b,c的大小关系是( )A.b>c>a
,则a,b,c的大小关系是( )A.b>c>a ![]() B.b>a>c
B.b>a>c ![]() C.c>a>b
C.c>a>b ![]() D.a>c>b9.在下列四组数中,不是勾股数的一组数是( )A.a=15,b=8,c=17 B.a=9,b=12,c=15 C.a=7,b=24,c=25 D.a=3,b=5,c=710.甲、乙、丙、丁四名射击选手,在相同条件下各射靶10次,他们的成绩统计如下表所示,若要从他们中挑选一位成绩最高且波动较小的选手参加射击比赛,那么一般应选( ) 甲乙丙丁平均数(环)99.599.5方差3.5445.4A.甲 B.乙 C.丙 D.丁11.在Rt△
D.a>c>b9.在下列四组数中,不是勾股数的一组数是( )A.a=15,b=8,c=17 B.a=9,b=12,c=15 C.a=7,b=24,c=25 D.a=3,b=5,c=710.甲、乙、丙、丁四名射击选手,在相同条件下各射靶10次,他们的成绩统计如下表所示,若要从他们中挑选一位成绩最高且波动较小的选手参加射击比赛,那么一般应选( ) 甲乙丙丁平均数(环)99.599.5方差3.5445.4A.甲 B.乙 C.丙 D.丁11.在Rt△![]() 中,
中,![]() ,
,![]() ,则
,则![]() ( )A.9 B.18 C.20 D.2412.用配方法解方程
( )A.9 B.18 C.20 D.2412.用配方法解方程![]() 时,配方结果正确的是( )A.
时,配方结果正确的是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 二、填空题(每题4分,满分20分,将答案填在答题纸上)13.如图所示,工人师傅做一个矩形铝合金窗框分下面三个步骤进行
二、填空题(每题4分,满分20分,将答案填在答题纸上)13.如图所示,工人师傅做一个矩形铝合金窗框分下面三个步骤进行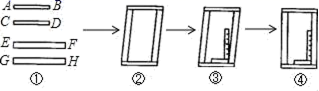 先截出两对符合规格的铝合金窗料(如图①所示),使AB=CD,EF=GH.(1)摆放成如图②的四边形,则这时窗框的形状是平行四边形,它的依据是 .(2)将直尺紧靠窗框的一个角(如图③),调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时(如图④,说明窗框合格,这时窗框是矩形,它的依据是 .14.已知点
先截出两对符合规格的铝合金窗料(如图①所示),使AB=CD,EF=GH.(1)摆放成如图②的四边形,则这时窗框的形状是平行四边形,它的依据是 .(2)将直尺紧靠窗框的一个角(如图③),调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时(如图④,说明窗框合格,这时窗框是矩形,它的依据是 .14.已知点![]() 及第二象限的动点
及第二象限的动点![]() ,且
,且![]() .设
.设![]() 的面积为
的面积为![]() ,则
,则![]() 关于
关于![]() 的函数关系式为________.15.勾股定理,是几何学中一颗光彩夺目的明珠,被称为“几何学的基石”.中国是发现和研究勾股定理最古老的国家之一.中国古代数学家称直角三角形为勾股形,较短的直角边称为勾,另一直角边称为股,斜边称为弦,所以勾股定理也称为勾股弦定理.三国时期吴国赵爽创制了“勾股圆方图”(如图)证明了勾股定理.在这幅“勾股圆方图”中,大正方形ABCD是由4个全等的直角三角形再加上中间的那个小正方形EFGH组成的.若小正方形的边长是1,每个直角三角形的短的直角边长是3,则大正方形ABCD的面积是_____.
的函数关系式为________.15.勾股定理,是几何学中一颗光彩夺目的明珠,被称为“几何学的基石”.中国是发现和研究勾股定理最古老的国家之一.中国古代数学家称直角三角形为勾股形,较短的直角边称为勾,另一直角边称为股,斜边称为弦,所以勾股定理也称为勾股弦定理.三国时期吴国赵爽创制了“勾股圆方图”(如图)证明了勾股定理.在这幅“勾股圆方图”中,大正方形ABCD是由4个全等的直角三角形再加上中间的那个小正方形EFGH组成的.若小正方形的边长是1,每个直角三角形的短的直角边长是3,则大正方形ABCD的面积是_____. 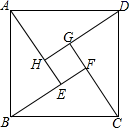 16.对于平面内任意一个凸四边形ABCD,现从以下四个关系式: ①AB=CD;②AD=BC;③AB∥CD;④∠A=∠C中任取两个作为条件,能够得出这个四边形ABCD是平行四边形的概率是_______.17.如图,把正方形AOBC 放在直角坐标系内,对角线AB、OC相交于点D.点C的坐标是(-4,4),将正方形AOBC沿x轴向右平移,当点D落在直线y=-2x+4上时,线段AD扫过的面积为_______ .
16.对于平面内任意一个凸四边形ABCD,现从以下四个关系式: ①AB=CD;②AD=BC;③AB∥CD;④∠A=∠C中任取两个作为条件,能够得出这个四边形ABCD是平行四边形的概率是_______.17.如图,把正方形AOBC 放在直角坐标系内,对角线AB、OC相交于点D.点C的坐标是(-4,4),将正方形AOBC沿x轴向右平移,当点D落在直线y=-2x+4上时,线段AD扫过的面积为_______ .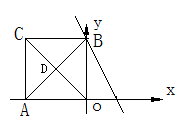 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)定义:如图(1),
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)定义:如图(1),![]() ,
,![]() ,
,![]() ,
,![]() 四点分别在四边形
四点分别在四边形![]() 的四条边上,若四边形
的四条边上,若四边形![]() 为菱形,我们称菱形
为菱形,我们称菱形![]() 为四边形
为四边形![]() 的内接菱形.动手操作:
的内接菱形.动手操作:
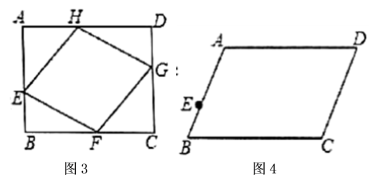 (1)如图2,网格中的每个小四边形都为正方形,每个小四边形的顶点叫做格点,由
(1)如图2,网格中的每个小四边形都为正方形,每个小四边形的顶点叫做格点,由![]() 个小正方形组成一个大正方形
个小正方形组成一个大正方形![]() ,点
,点![]() 、
、![]() 在格点上,请在图(2)中画出四边形
在格点上,请在图(2)中画出四边形![]() 的内接菱形
的内接菱形![]() ;特例探索:(2)如图3,矩形
;特例探索:(2)如图3,矩形![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上且
上且![]() ,四边形
,四边形![]() 是矩形
是矩形![]() 的内接菱形,求
的内接菱形,求![]() 的长度;拓展应用:(3)如图4,平行四边形
的长度;拓展应用:(3)如图4,平行四边形![]() ,
,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上且
上且![]() ,①请你在图4中画出平行四边形
,①请你在图4中画出平行四边形![]() 的内接菱形
的内接菱形![]() ,点
,点![]() 在边
在边![]() 上;②在①的条件下,当
上;②在①的条件下,当![]() 的长最短时,
的长最短时,![]() 的长为__________ 19.(5分)如图所示,已知直线L过点A(0,1)和B(1,0),P是x轴正半轴上的动点,OP的垂直平分线交L于点Q,交x轴于点M.(1)直接写出直线L的解析式;(2)设OP=t,△OPQ的面积为S,求S关于t的函数关系式;并求出当0<t<2时,S的最大值;(3)直线L1过点A且与x轴平行,问在L1上是否存在点C,使得△CPQ是以Q为直角顶点的等腰直角三角形?若存在,求出点C的坐标,并证明;若不存在,请说明理由.
的长为__________ 19.(5分)如图所示,已知直线L过点A(0,1)和B(1,0),P是x轴正半轴上的动点,OP的垂直平分线交L于点Q,交x轴于点M.(1)直接写出直线L的解析式;(2)设OP=t,△OPQ的面积为S,求S关于t的函数关系式;并求出当0<t<2时,S的最大值;(3)直线L1过点A且与x轴平行,问在L1上是否存在点C,使得△CPQ是以Q为直角顶点的等腰直角三角形?若存在,求出点C的坐标,并证明;若不存在,请说明理由.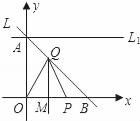 20.(8分)下岗职工王阿姨利用自己的﹣技之长开办了“爱心服装厂”,计划生产甲、乙两种型号的服装共40套投放到市场销售.已知甲型服装每套成本34元,售价39元;乙型服装每套成本42元,售价50元.服装厂预计两种服装的成本不低于1536元,不高于1552元. (1)问服装厂有哪几种生产方案? (2)按照(1)中方案生产,服装全部售出至少可获得利润多少元? (3)在(1)的条件下,服装厂又拿出6套服装捐赠给某社区低保户,其余34套全部售出,这样服装厂可获得利润27元.请直接写出服装厂这40套服装是按哪种方案生产的. 21.(10分)先化简,再求值:
20.(8分)下岗职工王阿姨利用自己的﹣技之长开办了“爱心服装厂”,计划生产甲、乙两种型号的服装共40套投放到市场销售.已知甲型服装每套成本34元,售价39元;乙型服装每套成本42元,售价50元.服装厂预计两种服装的成本不低于1536元,不高于1552元. (1)问服装厂有哪几种生产方案? (2)按照(1)中方案生产,服装全部售出至少可获得利润多少元? (3)在(1)的条件下,服装厂又拿出6套服装捐赠给某社区低保户,其余34套全部售出,这样服装厂可获得利润27元.请直接写出服装厂这40套服装是按哪种方案生产的. 21.(10分)先化简,再求值:![]() ÷(2+
÷(2+![]() ),其中x=
),其中x=![]() ﹣1. 22.(10分)如图,在四边形
﹣1. 22.(10分)如图,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 单位的速度向点
单位的速度向点![]() 运动,点
运动,点![]() 从点
从点![]() 同时出发,以每秒
同时出发,以每秒![]() 单位的速度向点
单位的速度向点![]() 运动,其中一个动点到达终点时,另一个动点也随之停止运动,设运动时间为
运动,其中一个动点到达终点时,另一个动点也随之停止运动,设运动时间为![]() 秒.
秒. (1)当
(1)当![]() 时,若以点
时,若以点![]() ,
,![]() 和点
和点![]() ,
,![]() ,
,![]() ,
,![]() 中的两个点为顶点的四边形为平行四边形,且线段
中的两个点为顶点的四边形为平行四边形,且线段![]() 为平行四边形的一边,求
为平行四边形的一边,求![]() 的值.(2)若以点
的值.(2)若以点![]() ,
,![]() 和点
和点![]() ,
,![]() ,
,![]() ,
,![]() 中的两个点为顶点的四边形为菱形,且线段
中的两个点为顶点的四边形为菱形,且线段![]() 为菱形的一条对角线,请直接写出
为菱形的一条对角线,请直接写出![]() 的值. 23.(12分)如图,已知矩形ABCD,用直尺和圆规进行如下操作:①以点A为圆心,以AD的长为半径画弧交BC于点E;②连接AE,DE;③作DF⊥AE于点F.根据操作解答下列问题:(1)线段DF与AB的数量关系是 .(2)若∠ADF=60°,求∠CDE的度数.
的值. 23.(12分)如图,已知矩形ABCD,用直尺和圆规进行如下操作:①以点A为圆心,以AD的长为半径画弧交BC于点E;②连接AE,DE;③作DF⊥AE于点F.根据操作解答下列问题:(1)线段DF与AB的数量关系是 .(2)若∠ADF=60°,求∠CDE的度数.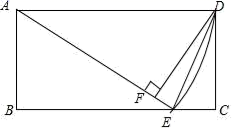 参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、A2、B3、A4、A5、B6、D7、A8、B9、D10、B11、B12、A 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、14、
参考答案 一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、A2、B3、A4、A5、B6、D7、A8、B9、D10、B11、B12、A 二、填空题(每题4分,满分20分,将答案填在答题纸上)13、14、![]()
![]() 15、2516、
15、2516、![]() 17、1 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、(1)详见解析;(2)3;(3)①详见解析;②
17、1 三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、(1)详见解析;(2)3;(3)①详见解析;②![]() 的长为
的长为![]() 19、(1)y=1﹣x;(2)
19、(1)y=1﹣x;(2)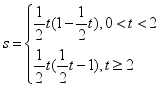 ,S有最大值
,S有最大值![]() ;(3)存在点C(1,1).20、(1)生产甲型服装16套,乙型24套或甲型服装17套,乙型23套或甲型服装1套,乙型服装22套;(2)至少可获得利润266元;(3)生产甲型服装16套,乙型服装24套21、当x=
;(3)存在点C(1,1).20、(1)生产甲型服装16套,乙型24套或甲型服装17套,乙型23套或甲型服装1套,乙型服装22套;(2)至少可获得利润266元;(3)生产甲型服装16套,乙型服装24套21、当x=![]() ﹣1时,原式=
﹣1时,原式=![]() =
=![]() .22、(1)当t=
.22、(1)当t=![]() 或4时,线段
或4时,线段![]() 为平行四边形的一边;(2)v的值是2或123、(1)DF=AB;(2)15°
为平行四边形的一边;(2)v的值是2或123、(1)DF=AB;(2)15°
相关试卷
这是一份2023-2024学年山东省德州武城县联考数学八年级第一学期期末质量检测试题含答案,共7页。试卷主要包含了答题时请按要求用笔,关于轴的对称点坐标为等内容,欢迎下载使用。
这是一份山东省聊城冠县联考2022-2023学年数学七年级第二学期期末质量检测试题含答案,共6页。试卷主要包含了下面是甲、乙两人10次射击成绩,若,则的值为,在平面直角坐标系中,点等内容,欢迎下载使用。
这是一份山东省临沂平邑县联考2022-2023学年数学七年级第二学期期末质量检测试题含答案,共7页。试卷主要包含了答题时请按要求用笔,下列变形错误的是等内容,欢迎下载使用。








