


2022-2023学年山东省泰安市名校七年级数学第二学期期末综合测试试题含答案
展开
这是一份2022-2023学年山东省泰安市名校七年级数学第二学期期末综合测试试题含答案,共7页。试卷主要包含了答题时请按要求用笔,若分式有意义,则的取值范围是,下列说法中,错误的是,式子有意义,则a的取值范围是等内容,欢迎下载使用。
2022-2023学年山东省泰安市名校七年级数学第二学期期末综合测试试题(时间:120分钟 分数:120分) 学校_______ 年级_______ 姓名_______ 注意事项:1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。2.答题时请按要求用笔。3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。5.保持卡面清洁,不要折暴、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。 一、选择题(每小题3分,共30分)1.直线![]() 与
与![]() 轴的交点坐标为( )A.
轴的交点坐标为( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 2.下列式子中,属于最简二次根式的是( )A.
2.下列式子中,属于最简二次根式的是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 3.下列各选项中因式分解正确的是( )A.
3.下列各选项中因式分解正确的是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 4.如图,在菱形ABCD中,点E,点F为对角线BD的三等分点,过点E,点F与BD垂直的直线分别交AB,BC,AD,DC于点M,N,P,Q,MF与PE交于点R,NF与EQ交于点S,已知四边形RESF的面积为5cm2,则菱形ABCD的面积是( )
4.如图,在菱形ABCD中,点E,点F为对角线BD的三等分点,过点E,点F与BD垂直的直线分别交AB,BC,AD,DC于点M,N,P,Q,MF与PE交于点R,NF与EQ交于点S,已知四边形RESF的面积为5cm2,则菱形ABCD的面积是( )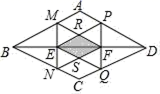 A.35cm2 B.40cm2 C.45cm2 D.50cm25.如图,
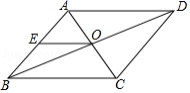
A.35cm2 B.40cm2 C.45cm2 D.50cm25.如图,![]()
![]() 的对角线AC,BD相交于点O,
的对角线AC,BD相交于点O,![]() 是AB中点,且AE+EO=4,则
是AB中点,且AE+EO=4,则![]() 的周长为
的周长为![]()
![]()
 A.20 B.16 C.12 D.86.若菱形的周长为16,高为2,则菱形两个邻角的比为( )A.6:1 B.5:1 C.4:1 D.3:17.若分式
A.20 B.16 C.12 D.86.若菱形的周长为16,高为2,则菱形两个邻角的比为( )A.6:1 B.5:1 C.4:1 D.3:17.若分式![]() 有意义,则
有意义,则![]() 的取值范围是
的取值范围是![]()
![]() A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 8.下列说法中,错误的是( )A.平行四边形的对角线互相平分B.对角线互相平分的四边形是平行四边形C.菱形的对角线互相垂直D.对角线互相垂直的四边形是菱形9.式子
8.下列说法中,错误的是( )A.平行四边形的对角线互相平分B.对角线互相平分的四边形是平行四边形C.菱形的对角线互相垂直D.对角线互相垂直的四边形是菱形9.式子![]() 有意义,则a的取值范围是( )A.
有意义,则a的取值范围是( )A.![]() 且
且![]() B.
B.![]() 或
或![]() C.
C.![]() 或
或![]() D.
D.![]() 且
且![]() 10.若关于
10.若关于![]() 的不等式组
的不等式组![]() 的整数解共5个,则
的整数解共5个,则![]() 的取值范围是( )A.
的取值范围是( )A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 二、填空题(本大题共有6小题,每小题3分,共18分)11.如图在平行四边形ABCD中,CD=2AD,BE⊥AD,点F为DC中点,连接EF、BF,下列结论:①∠ABC=2∠ABF;②EF=BF;③S四边形DEBC=2S△EFB;④∠CFE=3∠DEF,其中正确的有_____.
二、填空题(本大题共有6小题,每小题3分,共18分)11.如图在平行四边形ABCD中,CD=2AD,BE⊥AD,点F为DC中点,连接EF、BF,下列结论:①∠ABC=2∠ABF;②EF=BF;③S四边形DEBC=2S△EFB;④∠CFE=3∠DEF,其中正确的有_____.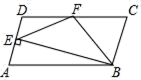 12.两个实数
12.两个实数![]() ,
,![]() ,规定
,规定![]() ,则不等式
,则不等式![]() 的解集为__________.13.如图,在矩形
的解集为__________.13.如图,在矩形![]() 中,
中,![]() ,对角线
,对角线![]() ,
,![]() 相交于点
相交于点![]() ,
,![]() 垂直平分
垂直平分![]() 于点
于点![]() ,则
,则![]() 的长为__________.
的长为__________.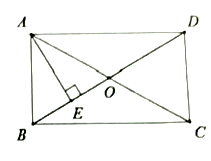 14.关于
14.关于![]() 的函数
的函数![]() (其中
(其中![]() )是一次函数,那么
)是一次函数,那么![]() =_______。15.若二次函数y=ax2+bx的图象开口向下,则a可以为_________(写出一个即可).16.已知一次函数y=kx+b的图象如图所示,则不等式kx+b≥4的解是______.
=_______。15.若二次函数y=ax2+bx的图象开口向下,则a可以为_________(写出一个即可).16.已知一次函数y=kx+b的图象如图所示,则不等式kx+b≥4的解是______.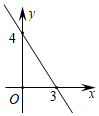 三、解下列各题(本大题共8小题,共72分)17.(8分)已知:△AOB和△COD均为等腰直角三角形,∠AOB=∠COD=90°.连接AD,BC,点H为BC中点,连接OH.
三、解下列各题(本大题共8小题,共72分)17.(8分)已知:△AOB和△COD均为等腰直角三角形,∠AOB=∠COD=90°.连接AD,BC,点H为BC中点,连接OH.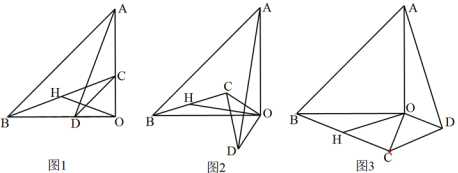 (1)如图1所示,求证:
(1)如图1所示,求证:![]() 且
且![]() (2)将△COD绕点O旋转到图2、图3所示位置时,线段OH与AD又有怎样的关系,并选择一个图形证明你的结论 18.(8分)如图,在矩形ABCD中,AE平分∠BAD,交BC于点E,过点E作EF⊥AD于点F,求证:四边形ABEF是正方形.
(2)将△COD绕点O旋转到图2、图3所示位置时,线段OH与AD又有怎样的关系,并选择一个图形证明你的结论 18.(8分)如图,在矩形ABCD中,AE平分∠BAD,交BC于点E,过点E作EF⊥AD于点F,求证:四边形ABEF是正方形.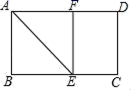 19.(8分)钓鱼岛是我国的神圣领土,中国人民维护国家领土完整的决心是坚定的,多年来,我国的海监、渔政等执法船定期开赴钓鱼岛巡视.某日,我海监船(A处)测得钓鱼岛(B处)距离为20海里,海监船继续向东航行,在C处测得钓鱼岛在北偏东45°的方向上,距离为10
19.(8分)钓鱼岛是我国的神圣领土,中国人民维护国家领土完整的决心是坚定的,多年来,我国的海监、渔政等执法船定期开赴钓鱼岛巡视.某日,我海监船(A处)测得钓鱼岛(B处)距离为20海里,海监船继续向东航行,在C处测得钓鱼岛在北偏东45°的方向上,距离为10![]() 海里,求AC的距离.(结果保留根号)
海里,求AC的距离.(结果保留根号)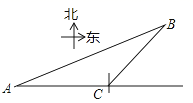 20.(8分)在一次社会调查活动中,小华收集到某“健步走运动”团队中20名成员一天行走的步数,记录如下:5640 6430 6520 6798 7325 8430 8215 7453 7446 6754 7638 6834 7326 6830 8648 8753 9450 9865 7290 7850 对这20个数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表:步数分组统计表 组别步数分组频数A5500≤x<65002B6500≤x<750010C7500≤x<8500mD8500≤x<95003E9500≤x<10500n
20.(8分)在一次社会调查活动中,小华收集到某“健步走运动”团队中20名成员一天行走的步数,记录如下:5640 6430 6520 6798 7325 8430 8215 7453 7446 6754 7638 6834 7326 6830 8648 8753 9450 9865 7290 7850 对这20个数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表:步数分组统计表 组别步数分组频数A5500≤x<65002B6500≤x<750010C7500≤x<8500mD8500≤x<95003E9500≤x<10500n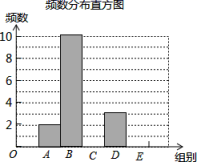 请根据以上信息解答下列问题:(1)填空:m= ______ ,n= ______ ;(2)补全频数发布直方图;(3)这20名“健步走运动”团队成员一天行走步数的中位数落在______ 组;(4)若该团队共有120人,请估计其中一天行走步数不少于7500步的人数. 21.(8分)如图,在平面直角坐标系中,四边形ABCD是矩形,AD∥x轴,A(
请根据以上信息解答下列问题:(1)填空:m= ______ ,n= ______ ;(2)补全频数发布直方图;(3)这20名“健步走运动”团队成员一天行走步数的中位数落在______ 组;(4)若该团队共有120人,请估计其中一天行走步数不少于7500步的人数. 21.(8分)如图,在平面直角坐标系中,四边形ABCD是矩形,AD∥x轴,A(![]() ,
,![]() ),AB=1,AD=1.
),AB=1,AD=1.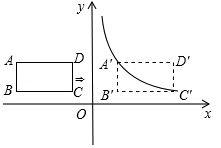 (1)直接写出B、C、D三点的坐标;(1)将矩形ABCD向右平移m个单位,使点A、C恰好同时落在反比例函数
(1)直接写出B、C、D三点的坐标;(1)将矩形ABCD向右平移m个单位,使点A、C恰好同时落在反比例函数![]() (
(![]() )的图象上,得矩形A′B′C′D′.求矩形ABCD的平移距离m和反比例函数的解析式. 22.(10分)如图,在▱ABCD中,各内角的平分线分别相交于点E,F,G,H.(1)求证:△ABG≌△CDE;(2)猜一猜:四边形EFGH是什么样的特殊四边形?证明你的猜想;(3)若AB=6,BC=4,∠DAB=60°,求四边形EFGH的面积.
)的图象上,得矩形A′B′C′D′.求矩形ABCD的平移距离m和反比例函数的解析式. 22.(10分)如图,在▱ABCD中,各内角的平分线分别相交于点E,F,G,H.(1)求证:△ABG≌△CDE;(2)猜一猜:四边形EFGH是什么样的特殊四边形?证明你的猜想;(3)若AB=6,BC=4,∠DAB=60°,求四边形EFGH的面积.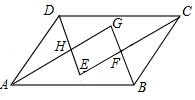 23.(10分)如图,在
23.(10分)如图,在![]() 中,点D、E分别是边BC、AC的中点,过点A作
中,点D、E分别是边BC、AC的中点,过点A作![]() 交DE的延长线于F点,连接AD、CF.
交DE的延长线于F点,连接AD、CF.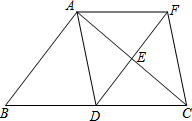 (1)求证:四边形ADCF是平行四边形;(2)当
(1)求证:四边形ADCF是平行四边形;(2)当![]() 满足什么条件时,四边形图ADCF是菱形?为什么? 24.(12分)在菱形ABCD中,AC是对角线.(1)如图①,若AB=6,则菱形ABCD的周长为______;若∠DAB=70º,则∠D的度数是_____;∠DCA的度数是____;(2)如图②,P是AB上一点,连接DP交对角线AC于点E,连接EB,求证: ∠APD=∠EBC.
满足什么条件时,四边形图ADCF是菱形?为什么? 24.(12分)在菱形ABCD中,AC是对角线.(1)如图①,若AB=6,则菱形ABCD的周长为______;若∠DAB=70º,则∠D的度数是_____;∠DCA的度数是____;(2)如图②,P是AB上一点,连接DP交对角线AC于点E,连接EB,求证: ∠APD=∠EBC.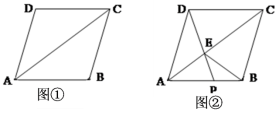 参考答案 一、选择题(每小题3分,共30分)1、B2、B3、D4、C5、B6、B7、A8、D9、A10、B 二、填空题(本大题共有6小题,每小题3分,共18分)11、①②③④12、
参考答案 一、选择题(每小题3分,共30分)1、B2、B3、D4、C5、B6、B7、A8、D9、A10、B 二、填空题(本大题共有6小题,每小题3分,共18分)11、①②③④12、![]() 13、
13、![]() 14、
14、![]() 、
、![]() 、
、![]() 15、a=−2(答案不唯一)16、x≤1 三、解下列各题(本大题共8小题,共72分)17、(1)详见解析;(2)详见解析.18、证明见解析.19、AC的距离为(10
15、a=−2(答案不唯一)16、x≤1 三、解下列各题(本大题共8小题,共72分)17、(1)详见解析;(2)详见解析.18、证明见解析.19、AC的距离为(10![]() ﹣10)海里20、(1)4;1;(2)见解析;(3)B;(4)48.21、(2)B(
﹣10)海里20、(1)4;1;(2)见解析;(3)B;(4)48.21、(2)B(![]() ,
,![]() ),C(
),C(![]() ,
,![]() ),D(
),D(![]() ,
,![]() );(2)m=4,
);(2)m=4,![]() .22、(1)证明见解析;(2)矩形;(3)
.22、(1)证明见解析;(2)矩形;(3)![]() .23、(1)见解析;(2)当△ABC是直角三角形,且∠BAC=90°时,四边形ADCF是菱形,理由见解析.24、(1)24;110°;35°;(2)见解析.
.23、(1)见解析;(2)当△ABC是直角三角形,且∠BAC=90°时,四边形ADCF是菱形,理由见解析.24、(1)24;110°;35°;(2)见解析.
相关试卷
这是一份山东省泰安市名校2023-2024学年数学八上期末调研试题含答案,共7页。试卷主要包含了已知,则,下列说法,分式的值为0,则,《九章算术》中记载,如图,图中直角三角形共有等内容,欢迎下载使用。
这是一份山东省泰安市2022-2023学年数学七年级第二学期期末经典试题含答案,共6页。试卷主要包含了7 的小数部分是等内容,欢迎下载使用。
这是一份2022-2023学年泰安市泰山区数学七年级第二学期期末综合测试试题含答案,共7页。










