


2022-2023学年山东省济南市育英中学数学七下期末质量跟踪监视模拟试题含答案
展开2022-2023学年山东省济南市育英中学数学七下期末质量跟踪监视模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
考生须知:
1.全卷分选择题和非选择题两部分,全部在答题纸上作答。选择题必须用2B铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。
2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。
3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。
一、选择题(每小题3分,共30分)
1.点P(-2,3)关于y轴的对称点的坐标是( )
A.(2,3) B.(-2,3) C.(2,-3) D.(-2,-3)
2.要使代数式![]() 有意义,实数
有意义,实数![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.若函数![]() 的图象在其象限内y的值随x值的增大而增大,则m的取值范围是( )
的图象在其象限内y的值随x值的增大而增大,则m的取值范围是( )
A.m>﹣2 B.m<﹣2
C.m>2 D.m<2
4.如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=2,BC=3,则图中阴影部分的面积为( )
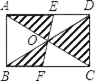
A.3 B.4 C.5 D.6
5.下列各组多项式中,没有公因式的是( )
A.ax﹣bx和by﹣ay B.3x﹣9xy和6y2﹣2y
C.x2﹣y2和x﹣y D.a+b和a2﹣2ab+b2
6.如图,已知一次函数![]() ,
,![]() 随着
随着![]() 的增大而增大,且
的增大而增大,且![]() ,则在直角坐标系中它的图象大致是( )
,则在直角坐标系中它的图象大致是( )
A.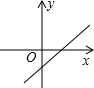 B.
B.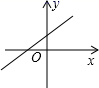 C.
C.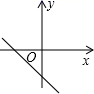 D.
D.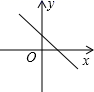
7.多项式![]() 与
与![]() 的公因式是( )
的公因式是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.甲、乙、丙、丁四人参加训练,近期的10次百米测试平均成绩都是13.2s,方差如下表:
选手 | 甲 | 乙 | 丙 | 丁 |
方差(s2) | 0.020 | 0.019 | 0.021 | 0.022 |
则这四人中发挥最稳定的是( )
A.甲 B.乙 C.丙 D.丁
9.在下列说法中:
①有一个外角是 120°的等腰三角形是等边三角形.
② 有两个外角相等的等腰三角形是等边三角形.
③ 有一边上的高也是这边上的中线的等腰三角形是等边三角形.
④ 三个外角都相等的三角形是等边三角形.
其中正确的有( )
A.1 个 B.2 个 C.3 个 D.4 个
10.下列式子属于最简二次根式的是( )
A.![]() B.
B.![]() C.
C.![]() (a>0) D.
(a>0) D.![]()
二、填空题(本大题共有6小题,每小题3分,共18分)
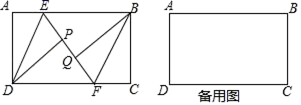
11.如图,在矩形ABCD中,AD=4,E,F分别为边AB,CD上一动点,AE=CF,分别以DE,BF为对称轴翻折△ADE,△BCF,点A,C的对称点分别为P,Q.若点P,Q,E,F恰好在同一直线上,且PQ=1,则EF的长为_____.
12.汽车行驶前油箱中有汽油52公升,已知汽车每百公里耗油8公升,油箱中的余油量Q(公升)(油箱中剩余的油量不能少于4公升)与它行驶的距离s(百公里)之间的函数关系式为_____(注明s的取值范围).
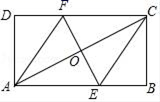
13.如图,在矩形ABCD中,对角线AC的垂直平分线分别交AB,CD于点E,F,连接AF,CE,如果∠BCE=26°,则∠CAF=_____
14.某公司招聘一名公关人员甲,对甲进行了笔试和面试,其面试和笔试的成绩分别为86分和90分,面试成绩和笔试成绩的权分别是6和4,则甲的平均成绩为__分.
15.中华文化源远流长,如图是中国古代文化符号的太极图,圆中的黑色部分和白色部分关于圆心中心对称.在圆内随机取一点,则此点取黑色部分的概率是__.

16.如果关于x的方程![]() 没有实数根,则k的取值范围为______.
没有实数根,则k的取值范围为______.
三、解下列各题(本大题共8小题,共72分)
17.(8分)在同一坐标系中,画出函数![]() 与
与![]() 的图像,观察图像写出当
的图像,观察图像写出当![]() 时,
时,![]() 的取值范围.
的取值范围.
18.(8分)(1)因式分解:2a3﹣8a2+8a;
(2)解不等式组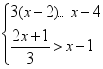 ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.
19.(8分)□ABCD中,AC=6,BD=10,动点P从B出发以每秒1个单位的速度沿射线BD匀速运动,动点Q从D出发以相同速度沿射线DB匀速运动,设运动时间为t秒.
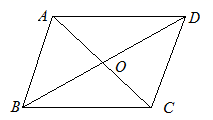
(1)当t =2时,证明以A、P、C、Q为顶点的四边形是平行四边形.
(2)当以A、P、C、Q为顶点的四边形为矩形时,直接写出t的值.
(3)设PQ=y,直接写出y与t的函数关系式.
20.(8分)(10分)已知E,F分别为正方形ABCD的边BC,CD上的点,AF,DE相交于点G,当E,F分别为边BC,CD的中点时,有:①AF=DE;②AF⊥DE成立.
试探究下列问题:
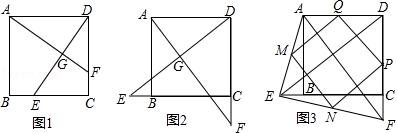
(1)如图1,若点E不是边BC的中点,F不是边CD的中点,且CE=DF,上述结论①,②是否仍然成立?(请直接回答“成立”或“不成立”),不需要证明)
(2)如图2,若点E,F分别在CB的延长线和DC的延长线上,且CE=DF,此时,上述结论①,②是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由;
(3)如图3,在(2)的基础上,连接AE和BF,若点M,N,P,Q分别为AE,EF,FD,AD的中点,请判断四边形MNPQ是“矩形、菱形、正方形”中的哪一种,并证明你的结论.
21.(8分)如图,在平面直角坐标系中,直线![]() 分别交两轴于点
分别交两轴于点![]() ,点
,点![]() 的横坐标为4,点
的横坐标为4,点![]() 在线段
在线段![]() 上,且
上,且![]() .
.
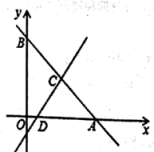
(1)求点![]() 的坐标;
的坐标;
(2)求直线![]() 的解析式;
的解析式;
(3)在平面内是否存在这样的点![]() ,使以
,使以![]() 为顶点的四边形为平行四边形?若存在,请求出点
为顶点的四边形为平行四边形?若存在,请求出点![]() 的坐标;若不存在,不必说明理由.
的坐标;若不存在,不必说明理由.
22.(10分) (1)因式分解:![]()
(2)解不等式组:![]() 并把解集在数轴上表示出来.
并把解集在数轴上表示出来.
23.(10分)已知一只纸箱中装有除颜色外完全相同的红色、黄色、蓝色乒乓球共100个.从纸箱中任意摸出一球,摸到红色球、黄色球的概率分别是0.2、0.1.
(1)试求出纸箱中蓝色球的个数;
(2)小明向纸箱中再放进红色球若干个,小丽为了估计放入的红球的个数,她将箱子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回箱子中,多次重复上述过程后,她发现摸到红球的频率在0.5附近波动,请据此估计小明放入的红球的个数.
24.(12分)计算:
(1)![]() (
(![]() ﹣
﹣![]() )+(
)+(![]() +1)1.
+1)1.
(1)(![]() ﹣
﹣![]() )÷
)÷![]()
参考答案
一、选择题(每小题3分,共30分)
1、A
2、B
3、B
4、A
5、D
6、A
7、B
8、B
9、B
10、B
二、填空题(本大题共有6小题,每小题3分,共18分)
11、2或![]()
12、Q=52﹣8s(0≤s≤6).
13、29°.
14、87.1.
15、![]()
16、![]()
三、解下列各题(本大题共8小题,共72分)
17、画图见解析,当![]() 时,
时,![]() 的取值范围为
的取值范围为![]() .
.
18、(1)![]() ;(2)1≤x<4,见解析
;(2)1≤x<4,见解析
19、 (1)见解析;(2) t =2或t =8;(3) y=-2t+10(0≤t≤5时),y=2y-10(t>5时).
20、(1)成立;(2)成立,理由见试题解析;(3)正方形,证明见试题解析.
21、(1)点![]() ;(2)
;(2)![]() ;(3)点
;(3)点![]() 的坐标是
的坐标是![]() ,
,![]() ,
,![]() .
.
22、 (1)![]() ;(2)
;(2)![]() .
.
23、(1)50;(2)2
24、(1)![]() ;(1)2.
;(1)2.
2023-2024学年山东省济南市实验中学数学八上期末质量跟踪监视试题含答案: 这是一份2023-2024学年山东省济南市实验中学数学八上期末质量跟踪监视试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,已知,如图反映的过程是等内容,欢迎下载使用。
2023-2024学年山东省济南市中学数学八上期末质量跟踪监视试题含答案: 这是一份2023-2024学年山东省济南市中学数学八上期末质量跟踪监视试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,在中,无理数的个数是,当时,代数式的值为,下列计算,正确的是,下列说法正确的是等内容,欢迎下载使用。
2022-2023学年黄冈中学数学七下期末质量跟踪监视模拟试题含答案: 这是一份2022-2023学年黄冈中学数学七下期末质量跟踪监视模拟试题含答案,共8页。试卷主要包含了答题时请按要求用笔,下列各式中,最简二次根式为等内容,欢迎下载使用。












