2022-2023学年山东省临沂莒南县联考七下数学期末达标检测试题含答案

2022-2023学年山东省临沂莒南县联考七下数学期末达标检测试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项:

1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内。

2．答题时请按要求用笔。

3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效。

4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。

5．保持卡面清洁，不要折暴、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、选择题(每小题3分,共30分)

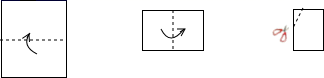
1．如图，把一个长方形的纸片对折两次，然后剪下一个角，为了得到一个钝角为的菱形，剪口与折痕所成的角的度数为（）

A． B．

C． D．

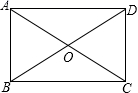
2．如图，在矩形ABCD中，对角线AC，BD相交于点O，若OA=2，则BD的长为(     )

A．4 B．3 C．2 D．1

3．某班主任老师为了对学生乱花钱的现象进行教育指导，对班里每位同学一周内大约花钱数额进行了统计，如下表：

根据这个统计表可知，该班学生一周花钱数额的众数、平均数是（  ）

A．15，14 B．18，14 C．25，12 D．15，12

4．下列各式属于最简二次根式的有（    ）

A． B． C． D．

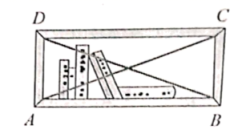
5．如图，用一根绳子检查一个书架的侧边是否和上、下底都垂直，只需要用绳子分别测量比较书架的两条对角线就可以判断，其数学依据是（   ）

A．三个角都是直角的四边形是矩形

B．对角线互相平分的四边形是平行四边形

C．对角线相等的平行四边形是矩形

D．对角线互相垂直平分的四边形是菱形

6．若x1、x2是x2+x﹣1＝0方程的两个不相等的实数根，则x1+x2﹣x1x2的值为（　　）

A．+1 B．﹣2 C．﹣2 D．0

7．如图，在△ABC中，点D、E分别是AB、AC的中点，下列结论不正确的是（　　）

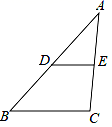
A．DE∥BC B．BC=2DE C．DE=2BC D．∠ADE=∠B

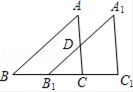
8．如图，△A1B1C1是由△ABC沿BC方向平移了BC长度的一半得到的，若△ABC的面积为20cm2，则四边形A1DCC1的面积为（　　）

A．10 cm2 B．12 cm2 C．15 cm2 D．17 cm2

9．点P（2，﹣3）关于y轴的对称点的坐标是（ ）

A．（2，3） B．（﹣2，﹣3） C．（﹣2，3） D．（﹣3，2）

10．小明在学习了正方形之后，给同桌小文出了道题，从下列四个条件：①AB=BC，②∠ABC=90°，③AC=BD，④AC⊥BD中选两个作为补充条件，使▱ABCD为正方形（如图），现有下列四种选法，你认为其中错误的是（ ）

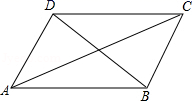
A．①② B．②③ C．①③ D．②④

二、填空题(本大题共有6小题，每小题3分，共18分)

11．因式分解：____________．

12．《九章算术》是中国传统数学最重要的著作，奠定了中国传统数学的基本框架，书中的算法体系至今仍在推动着计算机的发展和应用.《九章算术》中记载：今有户不知高、广，竿不知长、短.横之不出四尺，从之不出二尺，邪之适出.问户高、广、邪各几何?译文是：今有门不知其高、宽，有竿，不知其长、短，横放，竿比门宽长出尺；竖放，竿比门高长出尺；斜放，竿与门对角线恰好相等.问门高、宽、对角线长分别是多少?若设门对角线长为尺，则可列方程为__________．

13．如图是一个棱长为6的正方体盒子，一只蚂蚁从棱上的中点出发，沿盒的表面爬到棱上后，接着又沿盒子的表面爬到盒底的处．那么，整个爬行中，蚂蚁爬行的最短路程为__________．

14．a与5的和的3倍用代数式表示是________.

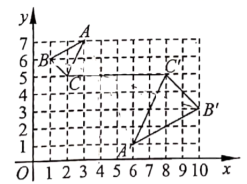
15．如图，在平面直角坐标系中，与关于点位似，且顶点都在格点上，则位似中心的坐标是__________．

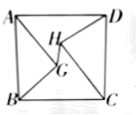
16．如图,正方形的边长为5，，连结，则线段的长为________．

三、解下列各题(本大题共8小题，共72分)

17．（8分）某城镇在对一项工程招标时，接到甲、乙两个工程队的投标书，每施工一天，需付甲队工程款2万元，付乙队工程款1.5万元.现有三种施工方案：（）由甲队单独完成这项工程，恰好如期完工；（）由乙队单独完成这项工程，比规定工期多6天；（）由甲乙两队后，剩下的由乙队单独做，也正好能如期完工.小聪同学设规定工期为天，依题意列出方程：.

（1）请将（）中被墨水污染的部分补充出来：________；

（2）你认为三种施工方案中，哪种方案既能如期完工，又节省工程款？说明你的理由.

18．（8分）已知：如图，AB是⊙O的直径，CD是⊙O的弦，且AB⊥CD，垂足为E．

（1）求证：BC=BD；

（2）若BC=15，AD= 20，求AB和CD的长．

19．（8分）在一次中学生田径运动会上，根据参加男子跳高初赛的运动员的成绩（单位：m），绘制出如下的统计图①和图②，请根据相关信息，解答下列问题：

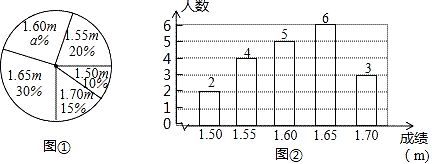
（Ⅰ）图1中a的值为　   　；

（Ⅱ）求统计的这组初赛成绩数据的平均数、众数和中位数；

（Ⅲ）根据这组初赛成绩，由高到低确定9人进入复赛，请直接写出初赛成绩为1.65m的运动员能否进入复赛．

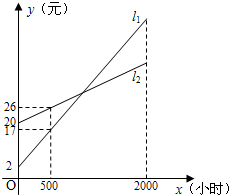
20．（8分）如图所示，，分别表示使用一种白炽灯和一种节能灯的费用（元，分别用y1与y2表示）与照明时间（小时）的函数图象，假设两种灯的使用寿命都是2000小时，照明效果一样.

（1）根据图象分别求出，对应的函数（分别用y1与y2表示）关系式；

（2）对于白炽灯与节能灯，请问该选择哪一种灯，使用费用会更省？

21．（8分）如图1，边长为的大正方形中有一个边长为的小正方形（），图2是由图1中阴影部分拼成的一个长方形．

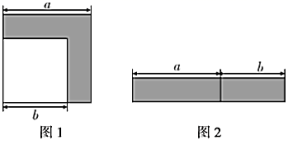
（1）观察图1、图2，当用不同的方法表示图形中阴影部分的面积时，可以获得一个因式分解公式，则这个公式是_______；

（2）如果大正方形的边长比小正方形的边长多3，它们的面积相差57，试利用（1）中的公式，求，的值．

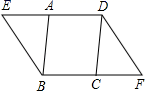
22．（10分）如图，在平行四边形ABCD中，E、F分别是DA、BC延长线上的点，且∠ABE＝∠CDF．

求证：（1）△ABE≌△CDF；

（2）四边形EBFD是平行四边形．

23．（10分）在水果销售旺季，某水果店购进一优质水果，进价为20元/千克，售价不低于20元/千克，且不超过32元/千克，根据销售情况，发现该水果一天的销售量y（千克）与该天的售价x（元/千克）满足如下表所示的一次函数关系．

（1）某天这种水果的售价为23.5元/千克，求当天该水果的销售量．

（2）如果某天销售这种水果获利150元，那么该天水果的售价为多少元？

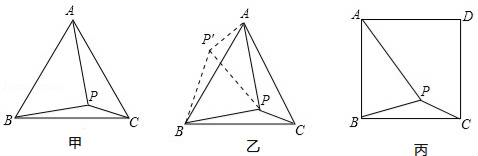
24．（12分）如图甲，在等边三角形ABC内有一点P，且PA＝2，PB＝，PC＝1，求∠BPC度数的大小和等边三角形ABC的边长．

解题思路是：将△BPC绕点B逆时针旋转60°，如图乙所示，连接PP′．

（1）△P′PB是   三角形，△PP′A是   三角形，∠BPC＝   °；

（2）利用△BPC可以求出△ABC的边长为   ．

如图丙，在正方形ABCD内有一点P，且PA＝，BP＝，PC＝1；

（3）求∠BPC度数的大小；

（4）求正方形ABCD的边长．

参考答案

一、选择题(每小题3分,共30分)

1、C

2、A

3、A

4、B

5、C

6、D

7、C

8、C

9、B

10、B

二、填空题(本大题共有6小题，每小题3分，共18分)

11、

12、．

13、15

14、3  （a+5）

15、

16、

三、解下列各题(本大题共8小题，共72分)

17、（1）合作5天；（2）方案（C）既能如期完工，又节省工程款.

18、（1）证明：∵AB为⊙O的直径，AB⊥CD，∴，∴

（2），

19、 (1) 25 ; (2) 这组初赛成绩数据的平均数是1.61.；众数是1.65；中位数是1.1；（3）初赛成绩为1.65 m的运动员能进入复赛.

20、（1）y1=x+2，y2=x+20（2）见解析

21、（1）；（2）a=11，b=1

22、（1）见解析；（2）见解析．

23、（1）当天该水果的销售量为2千克；（2）如果某天销售这种水果获利150元，该天水果的售价为3元．

24、（1）等边  直角  150°；（2）；（3）135°；（4） .