2022-2023学年安徽省宿州市泗县七年级数学第二学期期末质量跟踪监视试题含答案

2022-2023学年安徽省宿州市泗县七年级数学第二学期期末质量跟踪监视试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项：

1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。回答非选择题时，将答案写在答题卡上，写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交回。

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1．如图，OC平分∠AOB，点P是射线OC上的一点，PD⊥OB于点D，且PD=3，动点Q在射线OA上运动，则线段PQ的长度不可能是（ ）

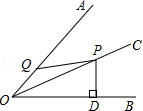
A．2 B．3 C．4 D．5

2．如图，小“鱼”与大“鱼”是位似图形，如果小“鱼”上一个“顶点”的坐标为（a，b），那么大“鱼”上对应“顶点”的坐标为（    ）．

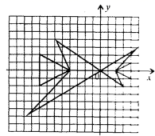
A．（－a，－2b） B．（－2a，－b） C．（－2a，－2b） D．（－2b，－2a）

3．如图，下列哪组条件不能判定四边形ABCD是平行四边形（　　）

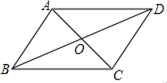
A．AB∥CD，AB＝CD B．AB∥CD，AD∥BC

C．OA＝OC，OB＝OD D．AB∥CD，AD＝BC

4．如图，在矩形中，，，点是边上一点，点是矩形内一点，，则的最小值是（    ）

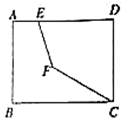
A．3 B．4 C．5 D．

5．五箱梨的质量（单位：千克）分别为：18，20，21，18，19，则这五箱梨质量的中位数和众数分是（  ）

A．20和18 B．20和19 C．18和18 D．19和18

6．下列各式：①，②，③，④中，最简二次根式有（   ）

A．1个 B．2个 C．3个 D．4个

7．一次函数y1=kx+b与y2=x+a的图象如图，则下列结论：①k＜1；②a＞1；③当x＜4时，y1＜y2；④b＜1．其中正确结论的个数是(   )

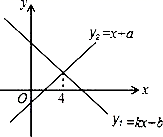
A．4个 B．3个 C．2个 D．1个

8．某校九年级“诗歌大会”比赛中，各班代表队得分如下（单位：分）：9，7，8，7，9，7，6，则各代表队得分的中位数是（    ）

A．9分    B．8分    C．7分    D．6分

9．如图，菱形ABCD的一边中点M到对角线交点O的距离为5cm，则菱形ABCD的周长为（　　）

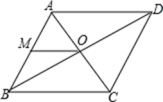
A．5cm B．10cm C．20cm D．40cm

10．下列图形既是轴对称图形，又是中心对称图形的是（　　）

A．三角形    B．菱形    C．角    D．平行四边形

11．已知四边形是平行四边形，下列结论中不正确的是（  ）

A．当时，它是菱形 B．当时，它是菱形

C．当时，它是矩形 D．当时，它是正方形

12．关于的一元二次方程，下列说法错误的是（    ）

A．方程无实数解

B．方程有一个实数解

C．有两个相等的实数解

D．方程有两个不相等的实数解

二、填空题（每题4分，满分20分，将答案填在答题纸上）

13．如图，在菱形中，，过的中点作，垂足为点，与的延长线相交于点，则_______，_______.

14．在菱形ABCD中，∠A=30°，在同一平面内，以对角线BD为底边作顶角为120°的等腰三角形BDE，则∠EBC的度数为 ．

15．若某组数据的方差计算公式是S2=[（7-）+（4-）2+（3-）2+（6-）2]，则公式中=______．

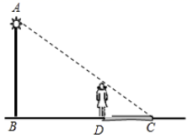
16．如图，身高1.6米的小明站在处测得他的影长为3米，影子顶端与路灯灯杆的距离为12米，则灯杆的高度为_______米．

17．如果顺次连接四边形的四边中点得到的新四边形是菱形，则与的数量关系是___．

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

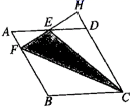
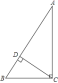
18．（5分）（1）如图，已知，在△ABC中，∠ACB=90°，CD⊥AB垂足为D，BC=6，AC=8，求AB与CD的长．

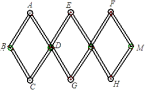
（2）如图，用3个全等的菱形构成活动衣帽架，顶点A、E、F、C、G、H是上、下两排挂钩，根据需要可以改变挂钩之间的距离（比如AC两点可以自由上下活动），若菱形的边长为13厘米，要使两排挂钩之间的距离为24厘米，并在点B、M处固定，则B、M之间的距离是多少？

19．（5分）武汉某文化旅游公司为了在军运会期间更好地宣传武汉，在工厂定制了一批具有浓郁的武汉特色的商品．为了了解市场情况，该公司向市场投放，型商品共件进行试销，型商品成本价元/件，商品成本价元/件，其中型商品的件数不大于型的件数，且不小于件，已知型商品的售价为元／件，型商品的售价为元／件，且全部售出．设投放型商品件，该公司销售这批商品的利润元．

（1）直接写出与之间的函数关系式：_______；

（2）为了使这批商品的利润最大，该公司应该向市场投放多少件型商品？最大利润是多少？

（3）该公司决定在试销活动中每售出一件型商品，就从一件型商品的利润中捐献慈善资金元，当该公司售完这件商品并捐献资金后获得的最大收益为元时，求的值．

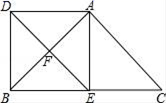
20．（8分）如图，E、F分别为△ABC的边BC、CA的中点，延长EF到D，使得DF=EF，连接DA、DB、AE．

（1）求证：四边形ACED是平行四边形；

（2）若AB=AC，试说明四边形AEBD是矩形．

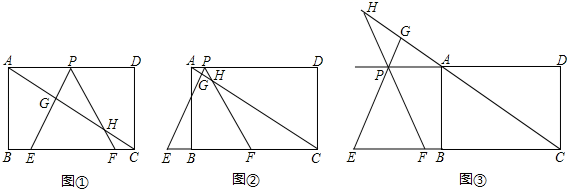
21．（10分）如图①，在矩形ABCD中，AB＝，BC＝3，在BC边上取两点E、F（点E在点F的左边），以EF为边所作等边△PEF，顶点P恰好在AD上，直线PE、PF分别交直线AC于点G、H．

（1）求△PEF的边长；

（2）若△PEF的边EF在线段CB上移动，试猜想：PH与BE有何数量关系？并证明你猜想的结论；

（3）若△PEF的边EF在射线CB上移动（分别如图②和图③所示，CF＞1，P不与A重合），（2）中的结论还成立吗？若不成立，直接写出你发现的新结论．

22．（10分）（1）计算：（1+2）（﹣）﹣（﹣）2

（2）因式分解：2mx2﹣8mxy+8my2

23．（12分）如图，利用一面长18米的墙，用篱笆围成一个矩形场地ABCD，设AD长为x米，AB长为y米，矩形的面积为S平方米．

(1)若篱笆的长为32米，求y与x的函数关系式，并直接写出自变量x的取值范围；

(2)在(1)的条件下，求S与x的函数关系式，并求出使矩形场地的面积为120平方米的围法．

参考答案

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1、A

2、C

3、D

4、A

5、D

6、A

7、D

8、C

9、D

10、B

11、D

12、B

二、填空题（每题4分，满分20分，将答案填在答题纸上）

13、1       

14、105°或45°

15、1．

16、

17、

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18、（1）AB=10，CD=4.8；（2）BM=30厘米.

19、（1）；（2）应投放件，最大利润为元；（3）满足条件时的值为

20、（1）证明见解析；（2）证明见解析

21、（1）△PEF的边长为2；（2）PH﹣BE=1，证明见解析；（3）结论不成立，当1＜CF＜2时，PH=1﹣BE，当2＜CF＜3时，PH=BE﹣1．

22、（1）﹣+1；（1）1m（x﹣1y）1．

23、 (1)y=-2x+32()；(2)当AB长为12米，AD长为10米时，矩形的面积为120平方米.