


2022-2023学年安徽省养鹿中学七下数学期末综合测试试题含答案
展开2022-2023学年安徽省养鹿中学七下数学期末综合测试试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.答题时请按要求用笔。
3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折暴、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题(每小题3分,共30分)
1.下列运算结果正确的是( )
A.![]() =﹣9 B.
=﹣9 B.![]() =2 C.
=2 C.![]() D.
D.![]()
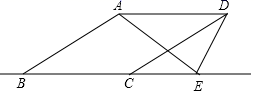
2.如图,在▱ABCD中,下列结论不一定正确的是( )
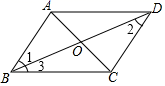
A.∠1=∠2 B.∠1=∠3 C.AB=CD D.∠BAD=∠BCD
3.小明乘出租车去体育场,有两条路线可供选择:路线一的全程是25千米,但交通比较拥堵,路线二的全程是30千米,平均车速比走路线一时的平均车速能提高80%,因此能比走路线一少用10分钟到达.若设走路线一时的平均速度为x千米/小时,根据题意,得
A.![]() B.
B.![]()
C.![]() D.
D.![]()
4.若正比例函数的图象经过点(2,4),则这个图象也必经过点( )
A.(2,1) B.(﹣1,﹣2) C.(1,﹣2) D.(4,2)
5.一元二次方程2x(x+1)=(x+1)的根是()
A.x=0 B.x=1
C.![]() D.
D.![]()
6.如图,点P是∠AOB的角平分线上一点,过点P作PC⊥OA于点C,且PC=3,则点P到OB的距离为( )
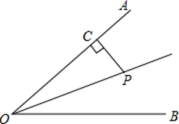
A.3 B.4 C.5 D.6
7.如图,直线![]() 的解析式为
的解析式为![]() ,直线
,直线![]() 的解析式为
的解析式为![]() ,则不等式
,则不等式![]() 的解集是( )
的解集是( )
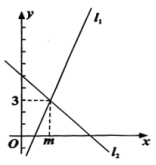
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.已知![]() ,
,![]() ,则
,则![]() 的结果为( )
的结果为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.无论x取什么值,下面的分式中总有意义的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.在▱ABCD中,AD=3cm,AB=2cm,则▱ABCD的周长等于( )
A.10cm B.6cm C.5cm D.4cm
二、填空题(本大题共有6小题,每小题3分,共18分)
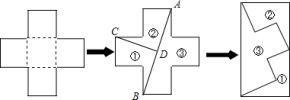
11.如图,五个全等的小正方形无缝隙、不重合地拼成了一个“十字”形,连接A、B两个顶点,过顶点C作CD⊥AB,垂足为D.“十字”形被分割为了①、②、③三个部分,这三个部分恰好可以无缝隙、不重合地拼成一个矩形,这个矩形的长与宽的比值为________.
12.如图,菱形![]() 中,
中,![]() ,点
,点![]() 是直线
是直线![]() 上的一点.已知
上的一点.已知![]() 的面积为6,则线段
的面积为6,则线段![]() 的长是_____.
的长是_____.
13.如图,在矩形![]() 中,
中,![]() ,点
,点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上,将
上,将![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在
落在![]() 上的点
上的点![]() 处,又将
处,又将![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在直线
落在直线![]() 与
与![]() 的交点
的交点![]() 处;
处;![]() ___________.
___________.

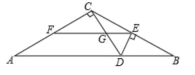
14.如图,已知EF是△ABC的中位线,DE⊥BC交AB于点D,CD与EF交于点G,若CD⊥AC,EF=8,EG=3,则AC的长为___________.
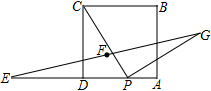
15.如图,正方形ABCD的边长为4,点E为AD的延长线上一点,且DE=DC,点P为边AD上一动点,且PC⊥PG,PG=PC,点F为EG的中点.当点P从D点运动到A点时,则CF的最小值为___________
16.一次函数![]() 的图像是由直线
的图像是由直线![]() __________________而得.
__________________而得.
三、解下列各题(本大题共8小题,共72分)
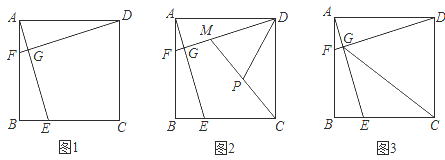
17.(8分)如图1,在正方形ABCD中,E、F分别是BC、AB上一点,且AF=BE,AE与DF交于点G.
(1)求证:AE=DF.
(2)如图2,在DG上取一点M,使AG=MG,连接CM,取CM的中点P.写出线段PD与DG之间的数量关系,并说明理由.
(3)如图3,连接CG.若CG=BC,则AF:FB的值为 .
18.(8分)如图,在平行四边形ABCD中,过点A作对角线BD的垂线,垂足为E,点F为AD的中点,连接FE并延长交BC于点G.
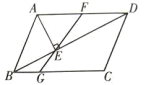
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,
,![]() ,求BG的长.
,求BG的长.
19.(8分)中国的高铁技术已经然走在了世界前列,2018年的“复兴号”高铁列车较“和谐号”速度增加每小时70公里.上海火车站到北京站铁路距离约为1400公里,如果选择“复兴号”高铁,全程可以少用1小时,求上海火车站到北京火车站的“复兴号”运行时间.
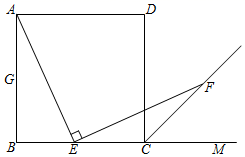
20.(8分)如图,四边形ABCD是正方形,点E是BC边上的点,∠AEF=90°,且EF交正方形外角的平分线CF于点F.
(1)如图①,当点E是BC边上任一点(不与点B、C重合)时,求证:AE=EF.
(2)如图②当点E是BC边的延长线上一点时,(1)中的结论还成立吗? (填成立或者不成立).
(3)当点E是BC边上任一点(不与点B、C重合)时,若已知AE=EF,那么∠AEF的度数是否发生变化?证明你的结论.
21.(8分)解方程:(1)![]() (2)解方程x2-4x+1=0
(2)解方程x2-4x+1=0
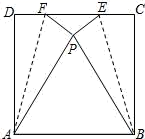
22.(10分)如图,将正方形ABCD折叠,使点C与点D重合于正方形内点P处,折痕分别为AF、BE,如果正方形ABCD的边长是2,那么△EPF的面积是_____.
23.(10分)计算
(1)计算:![]()
(2)分解因式:![]()
24.(12分)铜仁市积极推动某公园建设,通过旅游带动一方经济,计划经过若干年使公园绿化总面积新增450万平方米.自2016年初开始实施后,实际每年绿化面积是原计划的1.5倍,这样可以提前3年完成任务.
(1)求实际每年绿化面积是多少万平方米
(2)为加大公园绿化力度,市政府决定从2019年起加快绿化速度,要求不超过2年完成,那么实际平均每年绿化面积至少还要增加多少万平方米?
参考答案
一、选择题(每小题3分,共30分)
1、B
2、B
3、A
4、B
5、D
6、A
7、D
8、B
9、B
10、A
二、填空题(本大题共有6小题,每小题3分,共18分)
11、2
12、![]()
13、3
14、1
15、![]()
16、向上平移五个单位
三、解下列各题(本大题共8小题,共72分)
17、 (1) 见解析;(2) DG=![]() DP,理由见解析;(3) 1∶1.
DP,理由见解析;(3) 1∶1.
18、(1)见解析;(2)![]() .
.
19、4小时.
20、(1)见解析;(2)成立,理由见解析;(3)∠AEF=90°不发生变化.理由见解析.
21、(1)x1=1,![]() ;(2)
;(2)![]() ,
,![]() .
.
22、![]()
23、 (1)![]() ;(2)
;(2)![]() .
.
24、 (1)实际每年绿化面积为75万平方米;(2)平均每年绿化面积至少还要增加37.5万平方米.
安徽省养鹿中学2023-2024学年九年级数学第一学期期末联考试题含答案: 这是一份安徽省养鹿中学2023-2024学年九年级数学第一学期期末联考试题含答案,共8页。试卷主要包含了考生要认真填写考场号和座位序号,如图,是的外接圆,是直径,抛物线的对称轴为,已知sinα=,求α等内容,欢迎下载使用。
2023-2024学年安徽省养鹿中学数学八年级第一学期期末复习检测模拟试题含答案: 这是一份2023-2024学年安徽省养鹿中学数学八年级第一学期期末复习检测模拟试题含答案,共6页。试卷主要包含了考生要认真填写考场号和座位序号,下列运算结果为x-1的是,计算,下列条件等内容,欢迎下载使用。
河北省涉县鹿头中学2022-2023学年七下数学期末监测模拟试题含答案: 这是一份河北省涉县鹿头中学2022-2023学年七下数学期末监测模拟试题含答案,共7页。试卷主要包含了已知,则的值等于,一元二次方程的两根是等内容,欢迎下载使用。













