


2022-2023学年北京海淀区一零一中学数学七下期末复习检测试题含答案
展开2022-2023学年北京海淀区一零一中学数学七下期末复习检测试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
考生须知:
1.全卷分选择题和非选择题两部分,全部在答题纸上作答。选择题必须用2B铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。
2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。
3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。
一、选择题(每小题3分,共30分)
1.如图,在正方形ABCD外取一点E,连接AE、BE、DE,过A作AE的垂线交ED于点P,若AE=AP=1,PB=![]() ,下列结论:①△APD≌△AEB;②EB⊥ED;③PD=
,下列结论:①△APD≌△AEB;②EB⊥ED;③PD=![]() ,其中正确结论的序号是( )
,其中正确结论的序号是( )
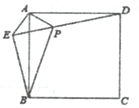
A.①② B.①③ C.②③ D.①②③
2.一名射击运动员连续打靶10次,命中的环数如图所示,这位运动员命中环数的众数与中位数分别为( )
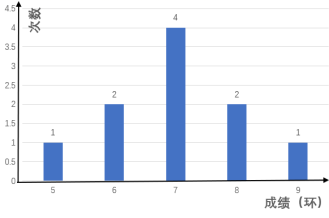
A.7与7 B.7与7.5 C.8与7.5 D.8与7
3.如图所示,▱ABCD的对角线AC,BD相交于点O,![]() ,
,![]() ,
,![]() ,▱ABCD的周长( )
,▱ABCD的周长( )
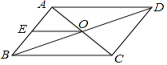
A.11 B.13 C.16 D.22
4.七巧板是一种古老的中国传统智力玩具.如图,在正方形纸板ABCD中,BD为对角线,E、F分别为BC、CD的中点,AP⊥EF分别交BD、EF于O、P两点,M、N分别为BO、DO的中点,连接MP、NF,沿图中实线剪开即可得到一副七巧板.若AB=1,则四边形BMPE的面积是( )
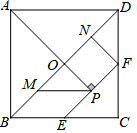
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.下列关系式中,y不是x的函数的是( )
A.y=x+1 B.y=![]() C.y=﹣2x D.|y|=x
C.y=﹣2x D.|y|=x
6.已知点![]() 的坐标是
的坐标是![]() ,则点
,则点![]() 关于
关于![]() 轴的对称点的坐标是( )
轴的对称点的坐标是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.二次函数y=ax2+bx+c(a≠1)的图象如图所示,对称轴是直线x=1,下列结论:
①ab<1;②b2>4ac;③a+b+c<1;④3a+c<1.其中正确的是( )
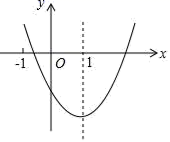
A.①④ B.②④ C.①②③ D.①②③④
8.一次函数y=2x﹣1的图象大致是( )
A. B.
B.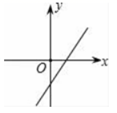 C.
C.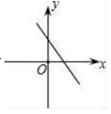 D.
D.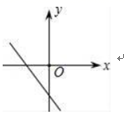
9.某百货商场试销一批新款衬衫,一周内销售情况如表所示。该商场经理想要了解哪种型号最畅销,那么他最关注的统计量是( )
型号 |
|
|
|
|
|
|
数量(件) |
|
|
|
|
|
|
A.众数 B.中位数 C.平均数 D.方差
10.下列多项式中能用完全平方公式分解的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(本大题共有6小题,每小题3分,共18分)
11.在设计人体雕像时,使雕像的上部(腰以上)与下部(腰以下)的高度比,等于下部与全部(全身)的高度比,可以增加视觉美感.按此比例,如果雕像的高度为 1m,那么它的下部应设计的高度为_____.
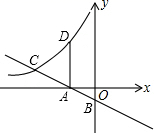
12.如图,直线y=-![]() x-
x-![]() 与x,y两轴分别交于A,B两点,与反比例函数y=
与x,y两轴分别交于A,B两点,与反比例函数y=![]() 的图象在第二象限交于点C.过点A作x轴的垂线交该反比例函数图象于点D.若AD=AC,则点D的纵坐标为___.
的图象在第二象限交于点C.过点A作x轴的垂线交该反比例函数图象于点D.若AD=AC,则点D的纵坐标为___.
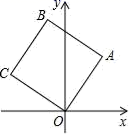
13.如图,将正方形OABC放在平面直角坐标系中,O是坐标原点,点A的坐标是(2,3),则C点坐标是_____.
14.已知一次函数y=kx+2的图象与x轴交点的横坐标为6,则当-3≤x≤3时,y的最大值是______.
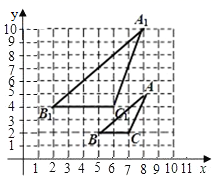
15.如图,已知图中的每个小方格都是边长为工的小正方形,每个小正方形的顶点称为格点,若![]() 与
与![]() 是位似图形,且顶点都在格点上,则位似中心的坐标是______.
是位似图形,且顶点都在格点上,则位似中心的坐标是______.
16.写一个无理数,使它与![]() 的积是有理数:________。
的积是有理数:________。
三、解下列各题(本大题共8小题,共72分)
17.(8分)某气球内充满了一定量的气体,当温度不变时,气球内气体的气压P(kPa)是气球体积V(m3)的反比例函数,且当V=0.8m3时,P=120kPa。
(1)求P与V之间的函数表达式;
(2)当气球内的气压大于100kPa时,气球将爆炸,为确保气球不爆炸,气球的体积应不小于多少?
18.(8分)解方程
(1)![]()
(2)![]()
(3)![]()
19.(8分)解方程:![]() -
-![]() =-1.
=-1.
20.(8分)解不等式组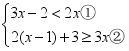 ,并将它的解集在数轴表示出来.
,并将它的解集在数轴表示出来.
![]()
21.(8分)某学校为了改善办学条件,计划购置一批电子白板和一批笔记本电脑,经投标,购买1块电子白板比买3台笔记本电脑多3000元,购买4块电子白板和5台笔记本电脑共需80000元.
(1)求购买1块电子白板和一台笔记本电脑各需多少元?
(2)根据该校实际情况,需购买电子白板和笔记本电脑的总数为396,要求购买的总费用不超过2700000元,并购买笔记本电脑的台数不超过购买电子白板数量的3倍,该校有哪几种购买方案?
(3)上面的哪种购买方案最省钱?按最省钱方案购买需要多少钱?
22.(10分)如图1,在平面直角坐标系中![]() 直线
直线![]() 与x轴、y轴相交于A、B两点,动点C在线段OA上,将线段CB绕着点C顺时针旋转
与x轴、y轴相交于A、B两点,动点C在线段OA上,将线段CB绕着点C顺时针旋转![]() 得到CD,此时点D恰好落在直线AB上时,过点D作
得到CD,此时点D恰好落在直线AB上时,过点D作![]() 轴于点E.
轴于点E.
![]() 求证:
求证:![]() ≌
≌![]() ;
;
![]() 如图2,将
如图2,将![]() 沿x轴正方向平移得
沿x轴正方向平移得![]() ,当直线
,当直线![]() 经过点D时,求点D的坐标及
经过点D时,求点D的坐标及![]() 平移的距离;
平移的距离;
![]() 若点P在y轴上,点Q在直线AB上
若点P在y轴上,点Q在直线AB上![]() 是否存在以C、D、P、Q为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的Q点坐;若不存在,请说明理由.
是否存在以C、D、P、Q为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的Q点坐;若不存在,请说明理由.
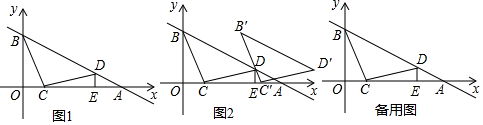
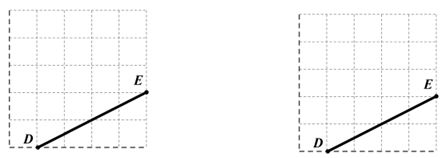
23.(10分)如图是由25个边长为1的小正方形组成的![]() 网格,请在图中画出以
网格,请在图中画出以![]() 为斜边的2个面积不同的直角三角形.(要求:所画三角形顶点都在格点上)
为斜边的2个面积不同的直角三角形.(要求:所画三角形顶点都在格点上)
24.(12分)已知反比例函数y=![]() 的图象经过点A(x1,y1)和B(x2,y2)(x1<x2)
的图象经过点A(x1,y1)和B(x2,y2)(x1<x2)
(1)若A(4,n)和B(n+![]() ,3),求反比例函数的表达式;
,3),求反比例函数的表达式;
(2)若m=1,
①当x2=1时,直接写出y1的取值范围;
②当x1<x2<0,p=![]() ,q=
,q=![]() ,试判断p,q的大小关系,并说明理由;
,试判断p,q的大小关系,并说明理由;
(3)若过A、B两点的直线y=x+2与y轴交于点C,连接BO,记△COB的面积为S,当![]() <S<1,求m的取值范围.
<S<1,求m的取值范围.
参考答案
一、选择题(每小题3分,共30分)
1、A
2、A
3、D
4、B
5、D
6、B
7、C
8、B
9、A
10、B
二、填空题(本大题共有6小题,每小题3分,共18分)
11、![]()
12、![]()
13、(﹣3,2).
14、1≤y≤1
15、(8,0)
16、答案不唯一,如![]()
三、解下列各题(本大题共8小题,共72分)
17、(1)P与V之间的函数表达式为![]() ;(2)为确保气球不爆炸,气球的体积应不小于0.96
;(2)为确保气球不爆炸,气球的体积应不小于0.96![]()
18、(1)![]() (2)
(2)![]() (3)
(3)![]()
19、x=-1
20、x≤1,将解集表示在数轴上见解析.
21、(1)购买1块电子白板需要15000元,一台笔记本电脑需要4000元(2)有三种购买方案:方案一:购买笔记本电脑295台,则购买电子白板101块;方案二:购买笔记本电脑296台,则购买电子白板100块;方案三:购买笔记本电脑297台,则购买电子白板99块.(3)当购买笔记本电脑297台、购买电子白板99块时,最省钱,共需费用2673000元
22、(1)证明见解析;(2)![]() 平移的距离是
平移的距离是![]() 个单位.(3)点Q的坐标为
个单位.(3)点Q的坐标为![]() 或
或![]() 或
或![]()
23、见解析
24、(1)y=![]() ;(2)①当0<x1<1时,y1>1,当x1<0时,y1<0;②p<q,见解析;(3)
;(2)①当0<x1<1时,y1>1,当x1<0时,y1<0;②p<q,见解析;(3)![]() <m<3或-1<m<-
<m<3或-1<m<-![]()
北京海淀区一零一中学2023-2024学年九年级数学第一学期期末复习检测模拟试题含答案: 这是一份北京海淀区一零一中学2023-2024学年九年级数学第一学期期末复习检测模拟试题含答案,共8页。试卷主要包含了考生必须保证答题卡的整洁,下列说法,错误的是,如图,函数y=kx+b等内容,欢迎下载使用。
2023-2024学年北京市海淀区师达中学数学八上期末检测模拟试题含答案: 这是一份2023-2024学年北京市海淀区师达中学数学八上期末检测模拟试题含答案,共7页。试卷主要包含了下列图标中是轴对称图形的是,在平面直角坐标系中,点P等内容,欢迎下载使用。
2022-2023学年重庆市綦江中学数学七下期末复习检测模拟试题含答案: 这是一份2022-2023学年重庆市綦江中学数学七下期末复习检测模拟试题含答案,共7页。试卷主要包含了使式子有意义的x的取值范围是.等内容,欢迎下载使用。













