


2022-2023学年北京海淀区七年级数学第二学期期末达标测试试题含答案
展开这是一份2022-2023学年北京海淀区七年级数学第二学期期末达标测试试题含答案,共6页。
2022-2023学年北京海淀区七年级数学第二学期期末达标测试试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项
1.考试结束后,请将本试卷和答题卡一并交回.
2.答题前,请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置.
3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符.
4.作答选择题,必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选涂其他答案.作答非选择题,必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效.
5.如需作图,须用2B铅笔绘、写清楚,线条、符号等须加黑、加粗.
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下列运算正确的是( )
A.![]() B.
B.![]() =4 C.
=4 C.![]() =3 D.
=3 D.![]()
2.如图,直线y=-x+m与y=nx+4n(n≠0)的交点的横坐标为-1.则下列结论:①m<0,n>0;②直线y=nx+4n一定经过点(-4,0);③m与n满足m=1n-1;④当x>-1时,nx+4n>-x+m,其中正确结论的个数是( )
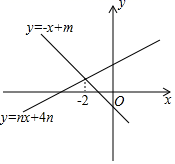
A.1个 B.1个 C.3个 D.4个
3.在一次数学课上,张老师出示了一个题目:“如图,▱ABCD的对角线相交于点O,过点O作EF垂直于BD交AB,CD分别于点F,E,连接DF,BE,请根据上述条件,写出一个正确结论.”其中四位同学写出的结论如下:
小青:OE=OF;小何:四边形DFBE是正方形;
小夏:S四边形AFED=S四边形FBCE;小雨:∠ACE=∠CAF,
这四位同学写出的结论中不正确的是( )
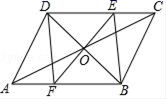
A.小青 B.小何 C.小夏 D.小雨
4.窗棂即窗格(窗里面的横的或竖的格)是中国传统木构建筑的框架结构设计.下列表示我国古代窗棂样式结构图案中,既是中心对称图形又是轴对称图形的是( )
A. B.
B. C.
C. D.
D.
5.若![]() ,
,![]() 两点都在直线
两点都在直线![]() 上,则
上,则![]() 与
与![]() 的大小关系是( )
的大小关系是( )
A.![]() B.
B.![]() C.
C.![]() D.无法确定
D.无法确定
6.已知![]() 是方程
是方程![]() 的一个根,则
的一个根,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.为了了解2013年昆明市九年级学生学业水平考试的数学成绩,从中随机抽取了1000名学生的数学成绩.下列说法正确的是( )
A.2013年昆明市九年级学生是总体 B.每一名九年级学生是个体
C.1000名九年级学生是总体的一个样本 D.样本容量是1000
8.如图,在平面直角坐标系中,正方形ABCD的顶点O在坐标原点,点B的坐标为(1,4),点A在第二象限,反比例函数![]() 的图象经过点A,则k的值是( )
的图象经过点A,则k的值是( )
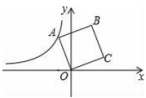
A.﹣2 B.﹣4 C.﹣![]() D.
D.![]()
9.下列函数:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() .其中,是一次函数的有( )
.其中,是一次函数的有( )
A.1个 B.2个 C.3个 D.4个
10.观察下列一组数:1,1,![]() ,
,![]() ,
,![]() ,
,![]() ,______。按照这组数的规律横线上的数是( )
,______。按照这组数的规律横线上的数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.如图,两个大小不同的正方形在同一水平线上,小正方形从图①的位置开始,匀速向右平移,到图③的位置停止运动.如果设运动时间为x,两个正方形重叠部分的面积为y,则下列图象中,能表示y与x的函数关系的图象大致是( )

A.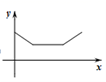 B.
B.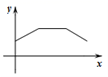 C.
C.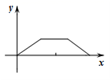 D.
D.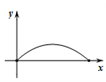
12.如图的![]() 中有一正方形
中有一正方形![]() ,其中
,其中![]() 在
在![]() 上,
上,![]() 在
在![]() 上,直线
上,直线![]() 分别交
分别交![]() 于
于![]() 两点. 若
两点. 若![]() ,则
,则![]() 的长度为()
的长度为()
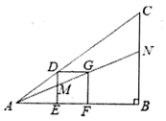
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13.因式分解:![]() =______.
=______.
14.在“童心向党,阳光下成长”的合唱比赛中,30个参赛队的成绩被分为5组,第1~4组的频数分别为2,10,7,8,则第5组的频率为________.
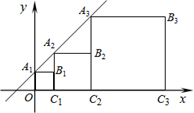
15.如图,在直角坐标系中,正方形A1B1C1O、 A2B2C2C1、A3B3C3C2、…、AnBnCnCn-1的顶点A1、A2、A3、…、An均在直线y=kx+b上,顶点C1、C2、C3、…、Cn在x轴上,若点B1的坐标为(1,1),点B2的坐标为(3,2),那么点A4的坐标为 ,点An的坐标为 .
16.在某校举行的“汉字听写”大赛中,六名学生听写汉字正确的个数分别为:35,31,32,31,35,31,则这组数据的众数是_____.
17.若分式![]() 的值为正数,则x的取值范围_____.
的值为正数,则x的取值范围_____.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
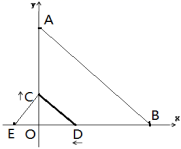
18.(5分)如图,已知点A(0,8)、B(8,0)、E(-2,0),动点 C从原点O出发沿OA方向以每秒1个单位长度向点A运动,动点D从点B出发沿BO方向以每秒2个单位长度向点O运动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动,设运动时间为t 秒。
(1)填空:直线AB的解析式是_____________________;
(2)求t的值,使得直线CD∥AB;
(3)是否存在时刻t,使得△ECD是等腰三角形?若存在,请求出一个这样的t值;若不存在,请说明理由。
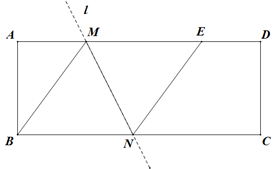
19.(5分)如图,在矩形ABCD中,AB=4,AD=10,点E在AD边上,已知B、E两点关于直线l对称,直线l分别交AD、BC边于点M、N,连接BM、NE.
(1)求证:四边形BMEN是菱形;
(2)若DE=2,求NC的长.
20.(8分)已知一次函数y=(3-k)x-2k2+18.
(1)当k为何值时,它的图象经过原点?
(2)当k为何值时,它的图象经过点(0,-2)?
(3)当k为何值时,它的图象平行于直线y=-x?
(4)当k为何值时,y随x增大而减小?
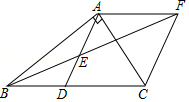
21.(10分)在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)证明四边形ADCF是菱形;
(2)若AC=4,AB=5,求菱形ADCF的面积.
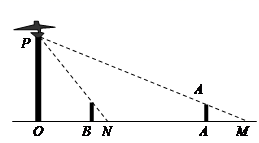
22.(10分)如图,路灯(![]() 点)距地面8米,身高1.6米的小明从距路灯的底部(
点)距地面8米,身高1.6米的小明从距路灯的底部(![]() 点 )20米的A点,沿OA所在的直线行走14米到B点时,身影的长度是变长了还是变短了;变长或变短了多少米.
点 )20米的A点,沿OA所在的直线行走14米到B点时,身影的长度是变长了还是变短了;变长或变短了多少米.
23.(12分)某商店准备进一批季节性小家电,单价40元.经市场预测,销售定价为52元时,可售出180个,定价每增加1元,销售量净减少10个;定价每减少1元,销售量净增加10个.因受库存的影响,每批次进货个数不得超过180个,商店若将准备获利2000元,则应进货多少个?定价为多少元?
参考答案
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、D
2、D
3、B
4、A
5、C
6、D
7、D
8、C
9、C
10、B
11、C
12、D
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13、2(x+3)(x﹣3).
14、0.1.
15、A4(7,8);An(2n-1-1,2n-1).
16、1
17、x>1
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18、![]()
19、(1)证明见解析; (2)NC=1.
20、 (1)见解析;(2) k=±![]() ;(1) k=4;(4) k>1.
;(1) k=4;(4) k>1.
21、见解析
22、变短了1.5米.
23、该商品每个定价为1元,进货100个.
相关试卷
这是一份北京市海淀区十一学校2023-2024学年数学八上期末达标测试试题含答案,共8页。试卷主要包含了考生必须保证答题卡的整洁,如图所示分别平分和,则的度数为,能使成立的x的取值范围是,下列计算正确的是等内容,欢迎下载使用。
这是一份北京市海淀区十一学校2022-2023学年数学七年级第二学期期末学业水平测试试题含答案,共7页。试卷主要包含了考生要认真填写考场号和座位序号,已知点在第二象限,则点在等内容,欢迎下载使用。
这是一份北京市海淀区十一学校2022-2023学年七年级数学第二学期期末达标检测模拟试题含答案,共6页。试卷主要包含了给出下列化简①,不能被整除等内容,欢迎下载使用。









