2022-2023学年北京陈经纶中学七年级数学第二学期期末复习检测试题含答案

这是一份2022-2023学年北京陈经纶中学七年级数学第二学期期末复习检测试题含答案，共7页。
2022-2023学年北京陈经纶中学七年级数学第二学期期末复习检测试题（时间：120分钟             分数：120分） 学校_______            年级_______        姓名_______ 注意事项1．考生要认真填写考场号和座位序号。2．试题所有答案必须填涂或书写在答题卡上，在试卷上作答无效。第一部分必须用2B 铅笔作答；第二部分必须用黑色字迹的签字笔作答。3．考试结束后，考生须将试卷和答题卡放在桌面上，待监考员收回。 一、选择题(每小题3分,共30分)1．某新品种葡萄试验基地种植了10亩新品种葡萄，为了解这些新品种葡萄的单株产量，从中随机抽查了4株葡萄，在这个统计工作中，4株葡萄的产量是(    )A．总体    B．总体中的一个样本    C．样本容量    D．个体2．如图，菱形ABCD的对角线AC、BD的长分别为6和8，则这个菱形的周长是（　　）A．20 B．24 C．40 D．483．下列各式成立的是（　　）A． B． C．（﹣）2＝﹣5 D．＝34．下列四组线段中，可以构成直角三角形的是（ ）A．4,5,6 B．1.5,2，2.5 C．2,3,4 D．1，， 35．一家鞋店在一段时间内销售了某种男鞋200双，各种尺码鞋的销售量如下表所示：尺码/厘米
 23
 23.5
 24
 24.5
 25
 25.5
 26
 销售量/双
 5
 10
 22
 39
 56
 43
 25
 一般来讲，鞋店老板比较关心哪种尺码的鞋最畅销，也就是关心卖出的鞋的尺码组成的一组数据是（）A．平均数 B．中位数 C．众数 D．方差6．在平行四边形ABCD中，AC=10，BD=6，则边长AB，AD的可能取值为（ 　 ）．A．AB=4，AD=4 B．AB=4，AD=7 C．AB=9，AD=2 D．AB=6，AD=27．如图所示，“数轴上的点并不都表示有理数，如图中数轴上的点P所表示的数是”，这种说明问题的方式体现的数学思想方法叫做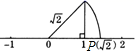（　　）A．代入法 B．换元法 C．数形结合 D．分类讨论8．如图，点O(0，0)，A(0，1)是正方形OAA1B的两个顶点，以OA1对角线为边作正方形OA1A2B1，再以正方形的对角线OA2作正方形OA2A3B2，…，依此规律，则点A7的坐标是(　　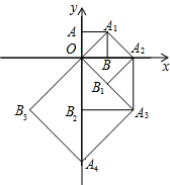)A．(-8，0) B．(8，-8) C．(-8，8) D．(0，16)9．下列函数中，表示y是x的正比例函数的是(　　)A．y＝﹣0.1x B．y＝2x2 C．y2＝4x D．y＝2x+110．如图，在平面直角坐标系中，线段AB的端点坐标为A（-2,4），B（4,2），直线y=kx-2与线段AB有交点，则K的值不可能是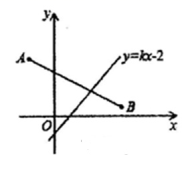（    ）A．-5 B．-2 C．3 D．5二、填空题(本大题共有6小题，每小题3分，共18分)11．若a，b都是实数，b＝+﹣2，则ab的值为_____．12．如图，点、分别是平行四边形的两边、的中点.若的周长是30，则的周长是_________.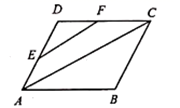13．如果关于x的方程kx2﹣6x+9＝0有两个相等的实数根，那么k的值为_____．14．如图，在△ABC中，∠B=∠C=60°，点D在AB边上，DE⊥AB，并与AC边交于点E．如果AD=1，BC=6，那么CE等于______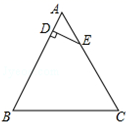．15．某种细菌病毒的直径为0.00005米，0.00005米用科学记数法表示为______米．16．如图，字母A所代表的正方形面积为____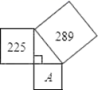．三、解下列各题(本大题共8小题，共72分)17．（8分）某个体户购进一批时令水果，20天销售完毕，他将本次的销售情况进行了跟踪记录，根据所记录的数据绘制如图所示的函数图象，其中日销售量y(千克)与销售时间x（天）之间的函数关系如图甲，销售单价P(元/千克)与销售时间x（天）之间的关系如图乙．（1）求y与x之间的函数关系式．（2）分别求第10天和第15天的销售金额．（3）若日销售量不低于24千克的时间段为“最佳销售期”，则此次销售过程中“最佳销售期”共有多少天？在此期间销售单价最高为多少元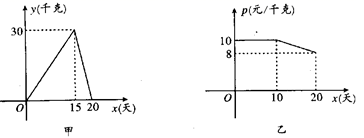？   18．（8分）某中学为了解该校学生的体育锻炼情况，随机抽查了该校部分学生一周的体育锻炼时间的情况，并绘制了如下两幅不完整的统计图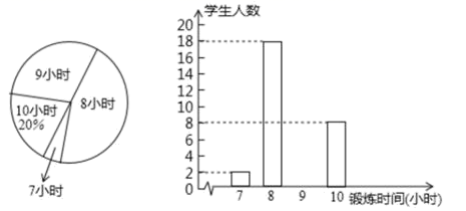：  根据以上信息解答以下问题：（1）本次抽查的学生共有多少名，并补全条形统计图；    （2）写出被抽查学生的体育锻炼时间的众数和中位数；    （3）该校一共有1800名学生，请估计该校学生一周体育锻炼时间不低于9小时的人数.   19．（8分）如图，一次函数的图象与反比例函数（为常数，且）的图象交于A（1，a）、B两点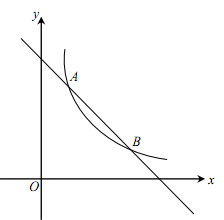．（1）求反比例函数的表达式及点B的坐标；（2）在x轴上找一点P，使PA+PB的值最小，求满足条件的点P的坐标及△PAB的面积．   20．（8分）已知点E是正方形ABCD内一点，连接AE，CE.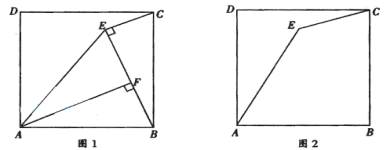(1)如图1，连接，过点作于点，若，，四边形的面积为.①证明:;②求线段的长.(2)如图2，若，，，求线段，的长.   21．（8分）如图，利用一面长18米的墙，用篱笆围成一个矩形场地ABCD，设AD长为x米，AB长为y米，矩形的面积为S平方米．(1)若篱笆的长为32米，求y与x的函数关系式，并直接写出自变量x的取值范围；(2)在(1)的条件下，求S与x的函数关系式，并求出使矩形场地的面积为120平方米的围法．   22．（10分）某工厂生产的件新产品,需要精加工后才能投放市场.现把精加工新产品的任务分给甲、乙两人，甲加工新产品的数量要比乙多.(1)求甲、乙两人各需加工多少件新产品；(2)已知乙比甲平均每天少加工件新产品，用时比甲多用天时间.求甲平均每天加工多少件新产品.   23．（10分）某市政府为了增强城镇居民抵御大病风险的能力，积极完善城镇居民医疗保险制度，纳入医疗保险的居民的大病住院医疗费用的报销比例标准如下表：医疗费用范围报销比例标准不超过8000元不予报销超过8000元且不超过30000元的部分50%超过30000元且不超过50000元的部分60%超过50000元的部分70%设享受医保的某居民一年的大病住院医疗费用为x元，按上述标准报销的金额为y元．（1）直接写出x≤50000时，y关于x的函数关系式，并注明自变量x的取值范围；（2）若某居民大病住院医疗费用按标准报销了20000元，问他住院医疗费用是多少元？   24．（12分）如图，△ABC中，AB=AC，∠BAC=90°，点D，E分别在AB，BC上，∠EAD=∠EDA，点F为DE的延长线与AC的延长线的交点．（1）求证：DE=EF；（2）判断BD和CF的数量关系，并说明理由；（3）若AB=3，AE=，求BD的长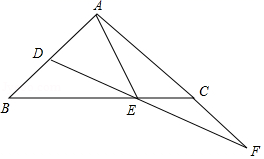．   参考答案 一、选择题(每小题3分,共30分)1、B2、A3、D4、B5、C6、B7、C8、C9、A10、B 二、填空题(本大题共有6小题，每小题3分，共18分)11、112、1513、1．14、415、1×10-116、1 三、解下列各题(本大题共8小题，共72分)17、 (1)当；(2)第10天：200元，第15天：270元；（3）最佳销售期有5天，最高为9.6元.18、（1）40，图形见解析；（2）众数是8，中位数是8.5；（3）900名19、（1），；（2）P，．20、（1）①证明见解析；②AE=；（2）,.21、 (1)y=-2x+32()；(2)当AB长为12米，AD长为10米时，矩形的面积为120平方米.22、（1）甲、乙两人分别需加工件、件产品；（2）甲平均每天加工件产品23、（1）①当x≤8000时，y=0；②当8000＜x≤30000时，y=0.5x﹣4000；③当30000＜x≤50000时，y=0.6x﹣7000；（2）1元．24、（1）证明见解析；（2证明见解析；（3）BD=1.