高考数学一轮复习考点测试刷题本36 二元一次不等式组与简单的线性规划(含答案解析)
展开2020高考数学(文数)考点测试刷题本36
二元一次不等式组与简单的线性规划
1.已知点(a,b)是平面区域内的任意一点,则3a-b的最小值为( )
A.-3 B.-2 C.-1 D.0
A.(-∞,2] B.[2,3] C.[3,+∞) D.[2,+∞)
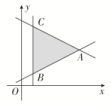
3.在如图所示的平面区域内有A(5,3),B(1,1),C(1,5)三点,若使目标函数z=ax+y(a>0)取得最大值的最优解有无穷多个,则实数a的值是( )
A. B. C.2 D.
4.已知实数x,y满足约束条件,则|y-x|的最大值是( )
A.2 B. C.4 D.3
A.2 B.3 C.4 D.5
6.某蔬菜收购点租用车辆,将100吨新鲜黄瓜运往某市销售,可供租用的卡车和农用车分别为10辆和20辆.若每辆卡车载重8吨,运费960元,每辆农用车载重2.5吨,运费360元,则蔬菜收购点运完全部黄瓜支出的最低运费为( )
A.11280元 B.12480元 C.10280元 D.11480元
7.设变量x,y满足约束条件,则目标函数z=3x+5y的最大值为( )
A.6 B.19 C.21 D.45
8.已知x,y满足约束条件,若z=ax+y的最大值为4,则a=( )
A.2 B.0.5 C.-2 D.-0.5
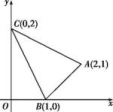
9.如图,△ABC及其内部的点组成的集合记为D,P(x,y)为D中任意一点,则z=2x+3y的最大值为 .
10.若x,y满足x+1≤y≤2x,则2y-x的最小值是________.
11.设变量x,y满足约束条件则的最大值为________.
12.某工厂制作仿古的桌子和椅子,需要木工和漆工两个工种,已知生产一把椅子需要木工4个工作时,漆工2个工作时;生产一张桌子需要木工8个工作时,漆工1个工作时.生产一把椅子的利润为1500元,生产一张桌子的利润为2000元,该厂每个月木工最多完成8000个工作时,漆工最多完成1300个工作时,根据以上条件,该厂安排生产每个月所能获得的最大利润是________元.
(1)求目标函数z=x-y+的最值;
(2)若目标函数z=ax+2y仅在点(1,0)处取得最小值,求a的取值范围.
(1)指出x,y的取值范围;
(2)平面区域内有多少个整点?
15.电视台播放甲、乙两套连续剧,每次播放连续剧时,需要播放广告.已知每次播放甲、乙两套连续剧时,连续剧播放时长、广告播放时长、收视人次如下表所示:
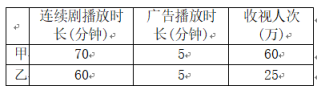
已知电视台每周安排的甲、乙连续剧的总播放时间不多于600分钟,广告的总播放时间不少于30分钟,且甲连续剧播放的次数不多于乙连续剧播放次数的2倍.分别用x,y表示每周计划播出的甲、乙两套连续剧的次数.
(1)用x,y列出满足题目条件的数学关系式,并画出相应的平面区域;
(2)问电视台每周播出甲、乙两套连续剧各多少次,才能使总收视人次最多?
16.某化肥厂生产甲、乙两种混合肥料,需要A,B,C三种主要原料.生产1车皮甲种肥料和生产1车皮乙种肥料所需三种原料的吨数如下表所示:
原料 肥料 | A | B | C |
甲 | 4 | 8 | 3 |
乙 | 5 | 5 | 10 |
现有A种原料200吨,B种原料360吨,C种原料300吨,在此基础上生产甲、乙两种肥料.
已知生产1车皮甲种肥料,产生的利润为2万元;生产1车皮乙种肥料,产生的利润为3万元.
分别用x,y表示计划生产甲、乙两种肥料的车皮数.
(1)用x,y列出满足生产条件的数学关系式,并画出相应的平面区域;
(2)问分别生产甲、乙两种肥料各多少车皮能够产生最大的利润?并求出最大利润.
解析:
根据题意可知(a,b)在如图阴影中,设z=3a-b.则b=3a-z,
所以-z可以理解为y=3x+t中的纵截距t.因而当y=3x+t过点(0,2)时,t最大为2.
即-z最大为2,所以z最小为-2.
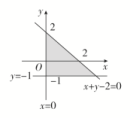
解析:作不等式组表示的平面区域,如图.平移直线x+3y=0到点A时,z取得最小值,
由解得点A,,所以zmin=+=2,无最大值.故选D.
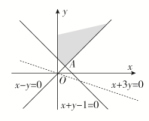
解析:
由题意知,当z=ax+y与直线AC重合时最优解有无穷多个.因为kAC=-,所以-a=-,即a=.
解析:画出不等式组表示的平面区域(如图),计算得A(1,2),B(4,1),
当直线z=x-y过点A时zmin=-1,过点B时zmax=3,则-1≤x-y≤3,则|y-x|≤3.
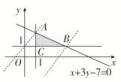
解析:
由不等式2x+y<6,得y<6-2x,且x>0,y>0,则当x=1时,0<y<4,则y=1,2,3,
此时整点有(1,1),(1,2),(1,3);当x=2时,0<y<2,则y=1,此时整点有(2,1);
当x=3时,y无解.故平面区域内的整点个数为4.故选C.
解析:
设租用的卡车和农用车分别为x辆和y辆,运完全部黄瓜支出的运费为z元,
则目标函数z=960x+360y,
此不等式组表示的可行域是△ABC(其中A(10,8),B(10,20),C(6.25,20))内横坐标
和纵坐标均为整数的点.当直线l:z=960x+360y经过点A(10,8)时,运费最低,
且其最低运费zmin=960×10+360×8=12480(元),选B.
解析:由变量x,y满足的约束条件画出可行域(如图中阴影部分所示).
作出基本直线l0:3x+5y=0,平移直线l0,当直线经过点A(2,3)时,z取最大值,
即zmax=3×2+5×3=21.故选C.
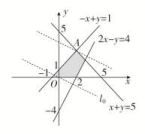
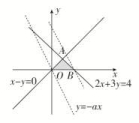
解析:作不等式组表示的平面区域如图.当直线l:y=-ax+z经过△AOB区域时,
l在y轴上的最大截距为4,则点B(2,0)为最优解,所以z=2a=4,即a=2,故选A.
解析:由题意可知直线z=2x+3y经过点A(2,1)时,z取得最大值,即zmax=2×2+3×1=7.
解析:
由x+1≤y≤2x作出可行域,如图中阴影部分所示.设z=2y-x,则y=x+z,
当直线y=x+z过A(1,2)时,z取得最小值3.
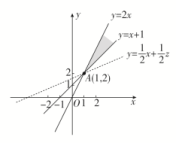
解析:
题设中的约束条件如图中阴影部分所表示的区域,则表示可行域内点P(x,y)
与B(0,-1)的连线的斜率,由图知,当P位于A(1,2)时,取得最大值=3.
解析:
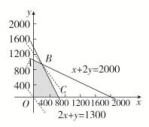
依题意,设每个月生产x把椅子、y张桌子,那么利润t=1500x+2000y.
其中x,y满足约束条件可行域如图中阴影部分所示,
对于不同的t值,t=1500x+2000y表示一组斜率为-的平行线,且t越大,
相应的直线位置越高;t越小,相应的直线位置越低.依题意,要求t的最大值,
需把直线t=1500x+2000y尽量地往上平移,又考虑到x,y的允许范围,
显然当直线通过点B时,处在这组平行线的最高位置,此时t取最大值.
由得点B(200,900),从而tmax=1500×200+2000×900=2100000(元),
即生产200把椅子、900张桌子可获得最大利润2100000元.
(1)作出可行域如图,可求得A(3,4),B(0,1),C(1,0).
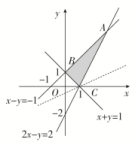
平移初始直线x-y=0,过A(3,4)取最小值-2,过C(1,0)取最大值1.
∴z的最大值为1,最小值为-2.
(2)直线ax+2y=z仅在点(1,0)处取得最小值,由图象可知-1<-<2,解得-4<a<2.
故所求a的取值范围是(-4,2).
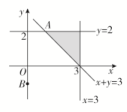
(1)不等式x-y+5≥0表示直线x-y+5=0上及右下方的点的集合.
x+y≥0表示直线x+y=0上及右上方的点的集合,
x≤3表示直线x=3上及左方的点的集合.
所以,不等式组
表示的平面区域如图所示.
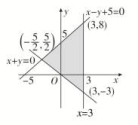
结合图中可行域得x∈,y∈[-3,8].
(2)由图形及不等式组知
当x=3时,-3≤y≤8,有12个整点;
当x=2时,-2≤y≤7,有10个整点;
当x=1时,-1≤y≤6,有8个整点;
当x=0时,0≤y≤5,有6个整点;
当x=-1时,1≤y≤4,有4个整点;
当x=-2时,2≤y≤3,有2个整点.
所以平面区域内的整点共有2+4+6+8+10+12=42(个).
(1)由已知,x,y满足的数学关系式为
即
该二元一次不等式组所表示的平面区域为图①中的阴影部分中的整数点.
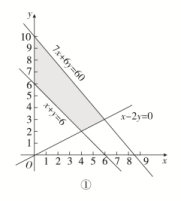
(2)设总收视人次为z万,则目标函数为z=60x+25y.
考虑z=60x+25y,将它变形为y=-x+,这是斜率为-,随z变化的一族平行直线.
为直线在y轴上的截距,当取得最大值时,z的值就最大.
又因为x,y满足约束条件,所以由图②可知,当直线z=60x+25y经过可行域上的点M时,
截距最大,即z最大.解方程组得则点M的坐标为(6,3).
所以,电视台每周播出甲连续剧6次、乙连续剧3次时,才能使总收视人次最多.
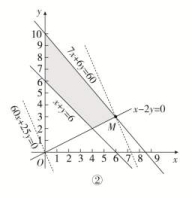
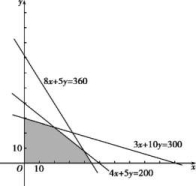
解析:该二元一次不等式组所表示的平面区域为图1中的阴影部分:
(2)设利润为z万元,则目标函数为z=2x+3y.考虑z=2x+3y,将它变形为y=-![]() x+
x+![]() ,这是斜率为-
,这是斜率为-![]() ,随z变化的一族平行直线.
,随z变化的一族平行直线.![]() 为直线在y轴上的截距,当
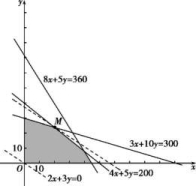
为直线在y轴上的截距,当![]() 取最大值时,z的值最大.又因为x,y满足约束条件,所以由图2可知,当直线z=2x+3y经过可行域上的点M时,截距
取最大值时,z的值最大.又因为x,y满足约束条件,所以由图2可知,当直线z=2x+3y经过可行域上的点M时,截距![]() 最大,即z最大.
最大,即z最大.
解方程组![]() 得点M的坐标为(20,24).所以zmax=2×20+3×24=112.
得点M的坐标为(20,24).所以zmax=2×20+3×24=112.
答:生产甲种肥料20车皮、乙种肥料24车皮时利润最大,且最大利润为112万元.
高考数学一轮复习考点测试刷题本39 复数(含答案解析): 这是一份高考数学一轮复习考点测试刷题本39 复数(含答案解析),共5页。
高考数学一轮复习作业本6.2 二元一次不等式(组)与简单的线性规划问题(含答案): 这是一份高考数学一轮复习作业本6.2 二元一次不等式(组)与简单的线性规划问题(含答案),共9页。
(艺术生)高考数学一轮复习讲与练:考点23 二元一次不等式(组)与简单的线性规划 (含解析): 这是一份(艺术生)高考数学一轮复习讲与练:考点23 二元一次不等式(组)与简单的线性规划 (含解析),共11页。试卷主要包含了二元一次不等式表示的平面区域,线性规划中的基本概念,利用线性规划求最值的基本步骤,设变量x,y满足约束条件等内容,欢迎下载使用。