2021届河北省张家口市高三上学期第一次质量检测试题 数学

这是一份2021届河北省张家口市高三上学期第一次质量检测试题 数学，共8页。
2021届河北省张家口市高三上学期第一次质量检测试题高三数学注意事项：1.本试卷共150分，考试时间120分钟。2.请将各题答案填在答题卡上。第I卷(选择题 共60分)一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。1.已知集合A＝{x|x2－2x<0}，B＝{x|x2＋3x－4>0}，则A∩(B)等于A.{x|0<x≤1}     B.{x|1≤x<2}     C.{x|0<x<2}     D.{x|－1≤x<2}2.下列函数中，既是奇函数又在定义域内递增的是A.f(x)＝e x－e－x     B.f(x)＝2x＋2－x     C.f(x)＝－     D.f(x)＝ln|x|3.已知△ABC中，AB＝7，BC＝5，CA＝3，则与的夹角是A.     B.     C.     D.4.若幂函数y＝f(x)的图象过点(27，3)，则函数f(x－1)－f2(x)的最大值为A.     B.－     C.－     D.－15.函数y＝x3＋log3(－x)的图象大致为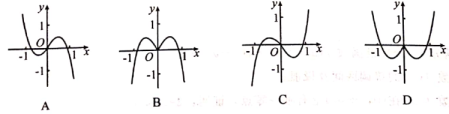6.已知f(x)是定义在R上的奇函数，当x≥0时，f(x)＝ex－1，若f(6－a2)>f(－a)，则实数a的取值范围是A.(－∞，－2)∪(3，＋∞)    B.(－3，2)    C.(－2，3)    D.(－∞，－3)∪(2，＋∞)7.已知f(x)＝2sinxcos－cos2x＋2，则f(x)的最小正周期和一个单调减区间分别为A.2π，[，]     B.π，[，]     C.2π，[－，]     D.π，[－，]8.在△ABC中，角A，B，C的对边分别为a，b，c，且cos2，则△ABC的形状为A.等边三角形     B..直角三角形     C.等腰三角形     D.等腰直角三角形二、选择题：本题共4小题，每小题5分，共20分。在每小题给出的四个选项中，有多项符合题目要求。全部选对的得5分，部分选对的得3分，有选错的得0分。9.已知集合P＝{x|0<x≤6}，Q＝{y|0≤y≤2}，下列从P到Q的各对应关系f是函数的是A.f：x→y＝x     B.f：x→y＝     C.f：x→y＝lnx     D.f：x→y＝10.下列有关向量命题，不正确的是A.若||＝||，则＝          B.已知≠，且·＝·，则＝C.若＝，＝，则＝     D.若＝，则||＝||且//11.下列命题中，正确的是A..在△ABC中，若A>B，则sinA>sinBB.在锐角三角形ABC中，不等式sinA>cosB恒成立C.在△ABC中，若acosA＝bcosB，则△ABC必是等腰直角三角形D.在△ABC中，若B＝60°，b2＝ac，则△ABC必是等边三角形12.将函数f(x)＝2sinx的图象向左平移个单位长度，然后纵坐标不变，横坐标变为原来的2倍，得到g(x)的图象，下列四个结论不正确的是A.函数g(x)在区间[0，]上为增函数B.将函数g(x)的图象向右平移个单位长度后得到的图象关于原点对称C.点(，0)是函数g(x)图象的一个对称中心D.函数g(x)在[π，2π]上的最大值为4第II卷(非选择题 共90分)三、填空题：本大题共4小题，每题5分，共20分。13.函数y＝log3(x2＋2x－8)的单调增区间是           。14.函数y＝ln(sinx)＋的定义域为           。15.已知向量与的夹角为60°。且||＝4，||＝3，若，且，则实数λ的值是           。16.若直线y＝kx＋b是曲线y＝ex－2的切线，也是曲线y＝ex－1的切线，则b＝         。四、解答题：本大题共6小题，17题10分，其余每题12分，共70分。17.(本小题满分10分)已知函数f(x)＝sinx＋cosx＋2sinxcosx＋2。(1)求f()的值；(2)求f(x)的最大值和最小值。18.(本小题满分12分)△ABC的三个内角A，B，C所对的边分别为a，b，c，asinAsinB－bsin2A＝a－b。(1)求；(2)若c2＝b2＋a2，求B。19.(本小题满分12分)已知α，β为锐角，cosβ＝，cos(α＋β)＝－。(1)求cos2α的值；(2)求tan(α－β)的值。20.(本小题满分12分)已知在△ABC中，角A、B、C的对边分别为a，b，c，外接圆半径为2，若，，·＝sin2C。(1)求角C的大小；(2)若sinA、sinC、sinB成等差数列，且＝18，求c的长。21.(本小题满分12分)已知函数f(x)＝cos2x＋sin(π－x)·cos(π＋x)－。(1)求函数f(x)在(0，π)上的单调递减区间；(2)在锐角△ABC中，内角A，B，C所对的边分别为a，b，c，已知f(A)＝－1，a＝2，bsinC＝asinA，求△ABC的周长。22.(本小题满分12分)设函数f(x)＝xex＋a(1－ex)＋1。(1)求函数f(x)的单调区间及极值；(2)若函数f(x)在(0，＋∞)上有唯一零点，证明：2<a<3。