高考数学一轮复习 精选习题：第四篇　平面向量 第1节 平面向量的概念及线性运算 Word版含解析

www.ks5u.com平面向量的概念及线性运算

【选题明细表】

基础巩固(时间:30分钟)

1.(2018·海淀模拟)下列说法正确的是(　C　)

(A)长度相等的向量叫做相等向量

(B)共线向量是在同一条直线上的向量

(C)零向量的长度等于0

(D)∥就是所在的直线平行于所在的直线

解析:长度相等且方向相同的向量叫做相等向量,故A不正确;方向相同或相反的非零向量叫做共线向量,但共线向量不一定在同一条直线上,故B不正确;显然C正确;当∥时,所在的直线与所在的直线可能重合,故D不正确.

2.已知向量a,b不共线,c=ka+b(k∈R),d=a-b.如果c∥d,那么(　D　)

(A)k=1且c与d同向

(B)k=1且c与d反向

(C)k=-1且c与d同向

(D)k=-1且c与d反向

解析:因为c∥d,所以存在实数λ,使得c=λd,

即ka+b=λ(a-b),

所以解得

此时c=-d.所以c与d反向.故选D.

3.已知向量a,b是两个不共线的向量,若向量m=4a+b与n=a-λb共线,则实数λ的值为(　B　)

(A)-4 (B)- (C) (D)4

解析:因为向量a,b是两个不共线的向量,向量m=4a+b与n=a-λb共线,

所以存在实数μ,使得4a+b=μ(a-λb),

即解得λ=-,故选B.

4.设D,E,F分别为△ABC的三边BC,CA,AB的中点,则+等于(　A　)

(A) (B) (C) (D)

解析: 因为D,E,F分别为BC,AC,AB的中点,

设AD,BE,CF交点为O,

则+=+=×2=

3=.故选A.

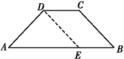
5.(2018·吉林大学附属中学摸底)在梯形ABCD中,=3,则等于(　D　)

(A)-+ (B)-+

(C)- (D)-+

解析: 在线段AB上取点E,使BE=DC,连接DE,则四边形BCDE为平行四边形,则==-=-.故选D.

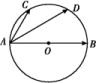
6. 如图所示,已知AB是圆O的直径,点C,D是半圆弧的两个三等分点,=a,=b,则等于(　D　)

(A)a-b 

(B)a-b

(C)a+b 

(D)a+b

解析:连接CD(图略),由点C,D是半圆弧的三等分点,得CD∥AB且==a,所以=+=b+a.

7.已知向量i与j不共线,且=i+mj,=ni+j,若A,B,D三点共线,则实数m,n应该满足的条件是(　C　)

(A)m+n=1 (B)m+n=-1

(C)mn=1 (D)mn=-1

解析:由A,B,D共线可设=λ(λ∈R),于是有i+mj=λ(ni+j)=λni+λj.又i,j不共线,因此即有mn=1.

8. 如图,点O是正六边形ABCDEF的中心,在分别以正六边形的顶点和中心为始点和终点的向量中,与向量相等的向量有　　　　　个. 

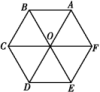
解析:根据正六边形的性质和相等向量的定义,易知与向量相等的向量有,,,共3个.

答案:3

9.已知向量e1,e2是两个不共线的向量,若a=2e1-e2与b=e1+λe2共线,则实数λ=　　　　　. 

解析:因为a与b共线,所以a=xb(x∈R),

故λ=-.

答案:-

能力提升(时间:15分钟)

10.在△ABC中,AB=2,BC=3,∠ABC=60°,AD为BC边上的高,O为AD的中点,若=λ+μ(λ,μ∈R),则λ+μ等于(　D　)

(A)1 (B) (C) (D)

解析:因为=+=+,

所以2=+,

即=+.

故λ+μ=+=.故选D.

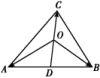
11.设O在△ABC的内部,D为AB的中点,且++2=0,则△ABC的面积与△AOC的面积的比值为(　B　)

(A)3 (B)4 (C)5 (D)6

解析:因为D为AB的中点,

则=(+),

又++2=0,

所以=-,

所以O为CD的中点.

又因为D为AB的中点,

所以S△AOC=S△ADC=S△ABC,则=4.

12.(2018·北京东城模拟)在直角梯形ABCD中,∠A=90°,∠B=30°,AB=2,BC=2,点E在线段CD上,若=+μ(μ∈R),则μ的取值范围是(　C　)

(A)[0,1]    (B)[0,]

(C)［0,］ (D)［,2]

解析: 如图所示,过点C作CF⊥AB,垂足为F.

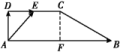
在Rt△BCF中,∠B=30°,

BC=2,

所以CF=1,BF=.

因为AB=2,所以AF=.

由四边形AFCD是平行四边形,

可得CD=AF==AB.

因为=+=+μ,

所以=μ.

因为∥,=,

所以0≤μ≤.故选C.

13.(2018·安徽示范性高中二模)△ABC内一点O满足+2+3=0,直线AO交BC于点D,则(　A　)

(A)2+3=0 (B)3+2=0

(C)-5=0 (D)5+=0

解析:因为△ABC内一点O满足+2+3=0,直线AO交BC于点D,

所以++=0.

令=+,则+=0,

所以B,C,E三点共线,A,O,E三点共线,所以D,E重合.

所以+5=0,

所以2+3=2-2+3-3=--5=0.故选A.

14. 如图所示,在△ABC中,点O是BC的中点.过点O的直线分别交直线AB,AC于不同的两点M,N,若=m,=n,则m+n的值为　  　. 

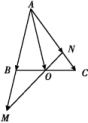
解析:=(+)=+.

因为M,O,N三点共线,

所以+=1.

所以m+n=2.

答案:2