高考数学一轮总复习课件第5章平面向量与复数第1讲平面向量的概念及线性运算（含解析）

这是一份高考数学一轮总复习课件第5章平面向量与复数第1讲平面向量的概念及线性运算（含解析），共44页。PPT课件主要包含了λ使b＝λa，答案BC，答案B，答案C，答案②，答案D，图5-1-2，答案A，答案3，题后反思等内容，欢迎下载使用。
向量 a(a≠0)与 b 共线的充要条件是存在唯一一个实数
题组一 走出误区1.( 多选题) 下列关于平面向量的说法中不正确的是
A.已知 a，b 均为非零向量，若 a∥b，则存在唯一的实数，使得 b＝λa
答案：b－a －a－b
考点一 平面向量的概念
①若两个向量相等，则它们的起点相同，终点相同；
ABCD 为平行四边形；
③a＝b 的充要条件是|a|＝|b|且 a∥b；
④已知λ，μ为实数，若λa＝μb，则 a 与 b 共线.其中真命题的序号是________.
解析：①错误，两个向量起点相同，终点相同，则两个向量相等；但两个向量相等，不一定有相同的起点和终点；
又 A，B，C，D 是不共线的四点，所以四边形 ABCD 为平行四边形；
③错误，当 a∥b 且方向相反时，即使|a|＝|b|，也不能得到 a＝b，所以|a|＝|b|且 a∥b 不是 a＝b 的充要条件，而是必要不充分条件；
④错误，当λ＝μ＝0 时，a 与 b 可以为任意向量，满足
λa＝μb，但 a 与 b 不一定共线.
【题后反思】向量有关概念的关键点(1)向量定义的关键是方向和长度.
(2)非零共线向量的关键是方向相同或相反，长度没有
(3)相等向量的关键是方向相同且长度相等.(4)单位向量的关键是长度都是一个单位长度.
(5)零向量的关键是长度为 0，规定零向量与任何向量
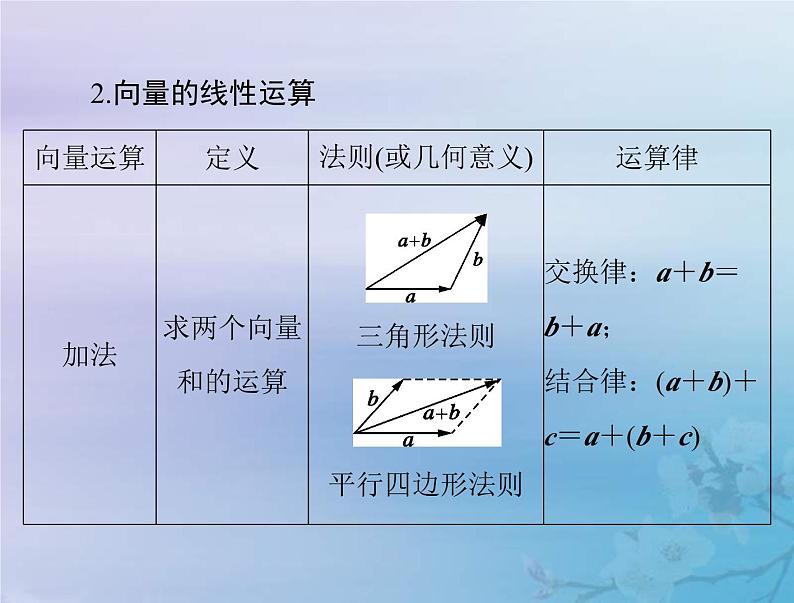
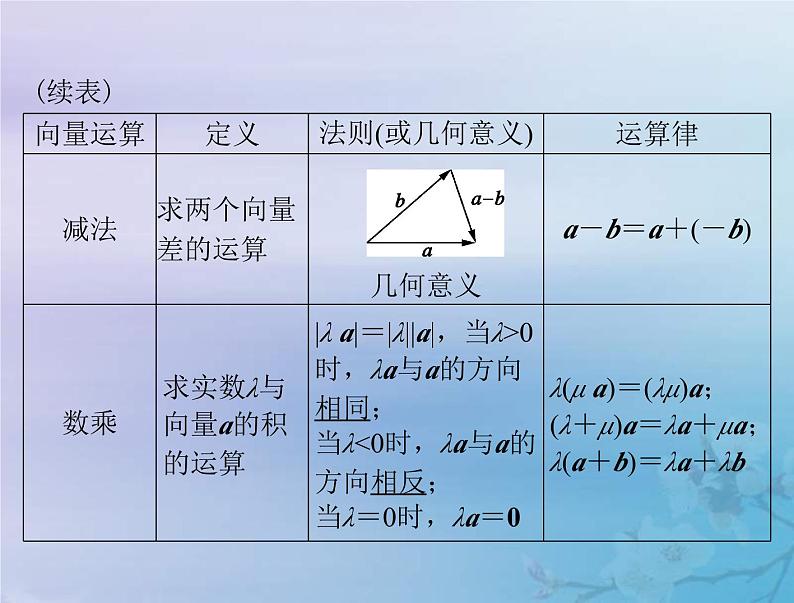
考点二 平面向量的线性运算考向 1 向量的线性运算
(2)在等腰梯形 ABCD 中，AB∥CD，AB＝2CD，E，F
分别为 BC，CD 的中点，则(
解析：根据题意，作图如图 5-1-2 所示.
考向 2 利用向量线性运算求参数[例2](1)如图 5-1-3，在平行四边形 ABCD 中，AC，BD
μ∈R)，则λ＋μ等于(
解析：∵E 为线段 AO 的中点，
(1)解题的关键在于熟练地找出图形中的相等向量，并
能熟练运用相反向量将加减法相互转化.
(2)用几个基本向量表示某个向量问题的基本技巧：①观察各向量的位置；②寻找相应的三角形或多边形；③运用法则找关系；④化简结果.
【考法全练】1.(考向 1)如图 5-1-4 所示，已知 AB 是圆 O 的直径
解析：连接 CD，由点 C，D 是半圆弧的两个三等分点，
考点三 共线向量定理及其应用
[例 3] 设两个非零向量 a 与 b 不共线.
(2)试确定实数 k，使 ka＋b 和 a＋kb 共线.
∴A，B，D 三点共线.
(2)解：∵ka＋b 与 a＋kb 共线，∴存在实数λ，使 ka＋b＝λ(a＋kb)，即 ka＋b＝λa＋λkb，∴(k－λ)a＝(λk－1)b.
∵a，b 是不共线的两个非零向量，∴k－λ＝λk－1＝0，
∴k2－1＝0，∴k＝±1.
(1)证明三点共线问题，可用向量共线解决，但应注意向量共线与三点共线的区别与联系，当两向量共线且有公共点时，才能得出三点共线.
(2)向量a，b共线是指存在不全为零的实数λ1，λ2，使
λ1a＋λ2b＝0 成立.
【变式训练】如图 5-1-5 所示，在△ABC 中，点 O 是 BC 的中点，过点 O 的直线分别交 AB，AC 所在直线于不同的两点 M，
解析：如图 D21 所示，连接 AO，
⊙数形结合法在向量中的应用
解析：以 O 为原点，OA 所在直线为 x 轴建立平面直角坐标系，如图 5-1-6 所示，图 5-1-6
解析：如图 D22 所示，作出示意图.