2020年江西省中考数学试卷与答案

这是一份2020年江西省中考数学试卷与答案，共9页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

2020年江西省中考数学试卷
一、选择题
1.－3的倒数是（ ）
A. 3 B. －3 C. D.
2.下列计算正确的是（ ）
A. B. C. D.
3.教育部近日发布了2019年全国教育经费执行情况统计快报，经初步统计，2019年全国教育经费总投入为50175亿元，比上年增长8.74%，将50175亿用科学记数法表示为（ ）
A. B. C. D.
4.如图，，则下列结论错误的是（ ）

A. B. C. D.
5.如图所示，正方体的展开图为（ ）

A. B.
C. D.
6.在平面直角坐标系中，点为坐标原点，抛物线与轴交于点，与轴正半轴交于点，连接，将向右上方平移，得到，且点，落在抛物线的对称轴上，点落在抛物线上，则直线的表达式为（ ）
A. B. C. D.
二、填空题
7.计算：_____．
8.若关于一元二次方程的一个根为，则这个一元二次方程的另一个根为_________．
9.公元前2000年左右，古巴比伦人使用的楔形文字中有两个符号（如图所示），一个钉头形代表1，一个尖头形代表10，在古巴比伦的记数系统中，人们使用的标记方法和我们当今使用的方法相同，最右边的数字代表个位，然后是十位，百位，根据符号记数的方法，右下面符号表示一个两位数，则这个两位数是__________．

10.祖冲之是中国数学史上第一个名列正史的数学家，他把圆周率精确到小数点后7位，这是祖冲之最重要的数学贡献，胡老师对圆周率的小数点后100位数字进行了如下统计：
数字
0
1
2
3
4
5
6
7
8
9
频数
8
8
12
11
10
8
9
8
12
14

那么，圆周率的小数点后100位数字的众数为__________．
11.如图，平分，，的延长线交于点，若，则的度数为__________．

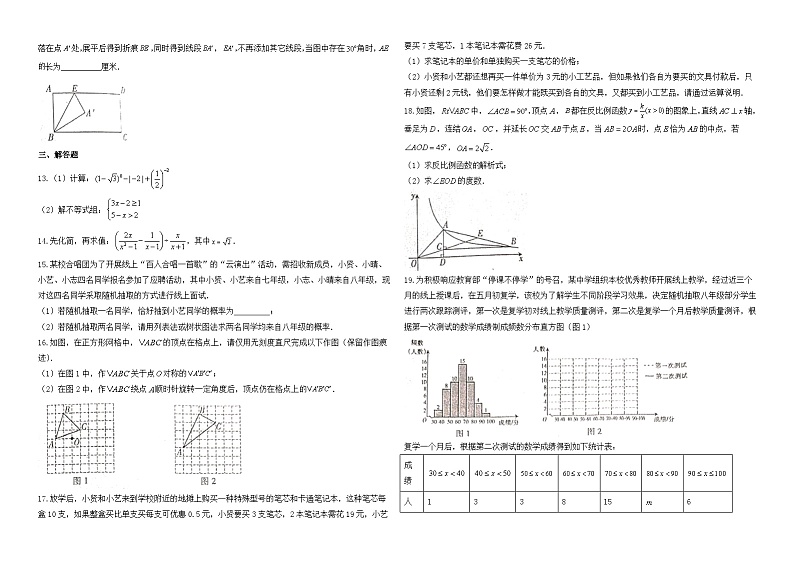
12.矩形纸片，长，宽，折叠纸片，使折痕经过点，交边于点，点落在点处，展平后得到折痕，同时得到线段，，不再添加其它线段，当图中存在角时，长为__________厘米．

三、解答题
13.（1）计算：
（2）解不等式组：
14.先化简，再求值：，其中．
15.某校合唱团为了开展线上“百人合唱一首歌”的“云演出”活动，需招收新成员，小贤、小晴、小艺、小志四名同学报名参加了应聘活动，其中小贤、小艺来自七年级，小志、小晴来自八年级，现对这四名同学采取随机抽取的方式进行线上面试．
（1）若随机抽取一名同学，恰好抽到小艺同学的概率为 ；
（2）若随机抽取两名同学，请用列表法或树状图法求两名同学均来自八年级的概率．
16.如图，在正方形网格中，的顶点在格点上，请仅用无刻度直尺完成以下作图（保留作图痕迹）．
（1）在图1中，作关于点对称的；
（2）在图2中，作绕点顺时针旋转一定角度后，顶点仍在格点上．

17.放学后，小贤和小艺来到学校附近的地摊上购买一种特殊型号的笔芯和卡通笔记本，这种笔芯每盒10支，如果整盒买比单支买每支可优惠0.5元，小贤要买3支笔芯，2本笔记本需花19元，小艺要买7支笔芯，1本笔记本需花费26元．
（1）求笔记本的单价和单独购买一支笔芯的价格；
（2）小贤和小艺都还想再买一件单价为3元的小工艺品，但如果他们各自为要买的文具付款后，只有小贤还剩2元钱，他们要怎样做才能既买到各自的文具，又都买到小工艺品，请通过运算说明．
18.如图，中，，顶点，都在反比例函数的图象上，直线轴，垂足为，连结，，并延长交于点，当时，点恰为的中点，若，．
（1）求反比例函数解析式；
（2）求的度数．

19.为积极响应教育部“停课不停学”的号召，某中学组织本校优秀教师开展线上教学，经过近三个月的线上授课后，在五月初复学，该校为了解学生不同阶段学习效果，决定随机抽取八年级部分学生进行两次跟踪测评，第一次是复学初对线上教学质量测评，第二次是复学一个月后教学质量测评，根据第一次测试的数学成绩制成频数分布直方图（图1）

复学一个月后，根据第二次测试的数学成绩得到如下统计表：
成绩







人数
1
3
3
8
15

6

根据以上图表信息，完成下列问题：
（1） ；
（2）请在图2中作出两次测试的数学成绩折线图，并对两次成绩作出对比分析（用一句话概述）；
（3）某同学第二次测试数学成绩为78分，这次测试中，分数高于78分的至少有 人，至多有 人；
（4）请估计复学一个月后该校800名八年级学生数学成绩优秀（80分及以上）的人数．
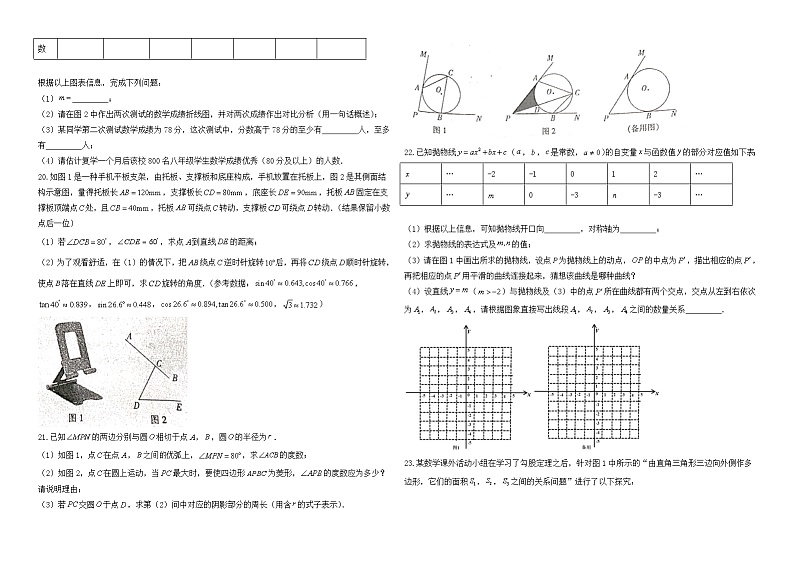
20.如图1是一种手机平板支架，由托板、支撑板和底座构成，手机放置在托板上，图2是其侧面结构示意图，量得托板长，支撑板长，底座长，托板固定在支撑板顶端点处，且，托板可绕点转动，支撑板可绕点转动．（结果保留小数点后一位）
（1）若，，求点到直线的距离；
（2）为了观看舒适，在（1）的情况下，把绕点逆时针旋转后，再将绕点顺时针旋转，使点落在直线上即可，求旋转的角度．（参考数据：，，，，）

21.已知的两边分别与圆相切于点，，圆的半径为．
（1）如图1，点在点，之间优弧上，，求的度数；
（2）如图2，点在圆上运动，当最大时，要使四边形为菱形，的度数应为多少？请说明理由；
（3）若交圆于点，求第（2）问中对应的阴影部分的周长（用含的式子表示）．

22.已知抛物线（，，是常数，）的自变量与函数值的部分对应值如下表：

…
-2
-1
0
1
2
…

…

0
-3

-3
…

（1）根据以上信息，可知抛物线开口向 ，对称轴为 ；
（2）求抛物线的表达式及的值；
（3）请在图1中画出所求的抛物线，设点为抛物线上的动点，的中点为，描出相应的点，再把相应的点用平滑的曲线连接起来，猜想该曲线是哪种曲线？
（4）设直线（）与抛物线及（3）中的点所在曲线都有两个交点，交点从左到右依次为，，，，请根据图象直接写出线段，，，之间的数量关系 ．

23.某数学课外活动小组在学习了勾股定理之后，针对图1中所示的“由直角三角形三边向外侧作多边形，它们的面积，，之间的关系问题”进行了以下探究：

类比探究
（1）如图2，在中，为斜边，分别以为斜边向外侧作，，，若，则面积，，之间的关系式为 ；
推广验证
（2）如图3，在中，为斜边，分别以为边向外侧作任意，，，满足，，则（1）中所得关系式是否仍然成立？若成立，请证明你的结论；若不成立，请说明理由；
拓展应用
（3）如图4，在五边形中，，，，，点在上，，，求五边形的面积．


2020年江西省中考数学试卷答案
1.D．2.D．3.A．4.C．5.A．6.B．
7.8.-2．9.25．10.9．11. 12.或．
13.解：（1）
=
=3；
（2）
由①得：x≥1
由②得：x＜3
所以该不等式组的解集为：1≤x＜3．
14.原式=，
=，
=
=，
把代入上式得，
原式=．
15.解：（1）由概率公式得：随机抽取一名同学，恰好抽到小艺同学的概率为，
故答案为：
（2）分别记小贤、小艺、小志、小晴为，
画树状图如下：

一共有种等可能的结果，其中两名同学均来自八年级的有种可能，
所以：两名同学均来自八年级的概率
16.（1）如图1所示；

（2）根据勾股定理可计算出AB=，AC=5，再作图，如图2所示．

17.（1）设单独购买一支笔芯的价格为x元，一本笔记本的价格为y元，
有，解得；
故笔记本的单价为5元，单独购买一支笔芯的价格为3元．
（2）两人共有金额19+26+2=47元，
若两人共购买10支笔芯（一盒），3本笔记本，由题目已知整盒买比单支买每支可优惠0.5元，
故两人买到各自的文具需要花费10×2.5+3×5=40（元），剩余47-40=7（元），可购买两件单价为3元的小工艺品；
故只有当两人一同购买笔芯，享受整盒购买优惠，即可能让他们既买到各自的文具，又都买到小工艺品．
18.（1）∵AD⊥x轴，∠AOD=45°，OA=，
∴AD=OD=2，
∴A(2，2)，
∵点A在反比例函数图象上，
∴k=2×2=4，
即反比例函数的解析式为．
(2)∵△ABC为直角三角形，点E为AB的中点，
∴AE=CE=EB，∠AEC=2∠ECB，
∵AB=2OA ，
∴AO=AE，
∴∠AOE=∠AEO=2∠ECB，
∵∠ACB=90°，AD⊥x轴，
∴BC//x轴，
∴∠ECB=∠EOD，
∴∠AOE=2∠EOD，
∵∠AOD=45°，
∴∠EOD=∠AOD=．
19.解：（1）由图1可知总人数为：2+8+10+15+10+4+1=50人，
所以m=50－1－3－3－8－15－6=14人；
（2）

通过第一次和第二次测试情况发现，复学初线上学习的成绩大部分在70分以下，复学后线下学习的成绩大部分在70分以上，说明线下上课的情况比线上好；
（3）由统计表可知，至少14+6=20人，至多15+14+6－1=34人；
（4）800×（人）
答：复学一个月后该校800名八年级学生数学成绩优秀（80分及以上）的人数为320人．
20.（1）如图所示，过点A作，，，
则,

∵，，
∴，
又∵，，
∴，，
∴，
∴,
∴，
又∵,，
∴mm，
∴．
∴点到直线的距离是．
（2）如图所示，

根据题意可得，，，
∴，
∴，
根据（1）可得，
∴旋转的角度=．
21.解：（1）如图1，连接OA、OB
∵PA，PB为⊙O的切线
∴∠PAO=∠PBO=90°
∴∠AOB+∠MPN=180°
∵∠MPN=80°
∴∠AOB=180°-∠MPN=100°
∴∠AOB=100°=∠ACB=50°；

（2）当∠APB=60°时，四边形APBC为菱形，理由如下：
如图2：连接OA、OB
由（1）可知∠AOB+∠APB=180°
∵∠APB=60°
∴∠AOB=120°
∴∠ACB=60°=∠APB
∵点C运动到PC距离最大
∴PC经过圆心
∵PA、PB为⊙O的切线
∴四边形APBC为轴对称图形
∵PA=PB，CA=CB，PC平分∠APB和∠ACB
∴∠APB=∠ACB=60°
∴∠APO=∠BPO=∠ACP=∠BCP=30°
∴PA =PB=CA =CB
∴四边形APBC为菱形；

（3）∵⊙O的半径为r
∴OA=r，OP=2 r
∴AP=r，PD=r
∵∠AOP=60°
∴
∴C阴影．
22.（1）由表可知：；，x=2,y=-3可知抛物线开后方向向上；
由表可知：；，可知抛物线的对称轴为：
故答案为：上，
（2）由表可知：代入点得
，解得
∴抛物线的表达式为：
当时，
当时，
（3）作图如下：

OP中点连接后的图象如图所示：为抛物线

（4）如图所示：可得

23.（1）∵△ABC是直角三角形，
∴，
∵△ABD、△ACE、△BCF均为直角三角形，且，
∴∽∽，
∴，，
∴
∴得证．
（2）成立，理由如下：
∵△ABC是直角三角形，
∴，
∵在△ABD、△ACE、△BCF中，，，
∴∽∽，
∴，，
∴
∴得证．
（3）过点A作AHBP于点H，连接PD，BD，
∵，，
∴，，
∵，
∴，
∴PH=AH=，
∴，，
∴，
∵，ED=2，
∴，，
∴，
∵，
∴△ABP∽△EDP，
∴，，
∴，，
∴，
，
∵，
∴
∵，
∴
∵
∴△ABP∽△EDP∽△CBD
∴
故最后答案为．