专项突破4-因数和倍数的认识六年级下册小升初数学专项培优卷（含解析）

专项突破4   因数和倍数的认识

【考点导图】

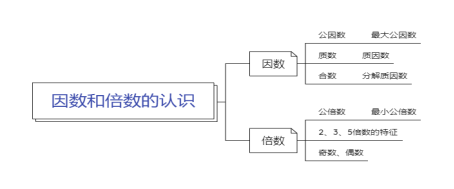
【考点精讲】

【典型题目】

一．选择题（共18小题）

1．4+x的和是偶数，x一定是（　　）

A．奇数 B．偶数 C．合数 D．质数

2．6的所有因数是1、2、3、6，这几个因数之间的关系是1+2+3＝6，像这样的数叫做完全数（也叫完美数）。下面的数中（　　）是完全数。

A．24 B．28 C．36 D．49

3．6的因数有1、2、3、6，这几个因数的关系是1+2+3＝6，像这样的数叫做完美数。下列（　　）是完美数。

A．9 B．12 C．15 D．28

4．下面各数中，既是6的倍数，又是54的因数的是（　　）

A．9 B．12 C．18 D．30

5．从这四张数字卡片中任选两张，摆成不同的两位数。其中2和3的公倍数有（　　）个。

A．3 B．4 C．5

6．淘气买圆珠笔花了10元，笑笑买圆珠笔花了8元。如果他们买的圆珠笔的单价是一样的，那么这种圆珠笔的单价最高是（　　）元。（淘气和笑笑买圆珠笔的单价和数量都是整数）。

A．2 B．4 C．20 D．40

7．甲数是乙数的倍数，甲、乙两数的最大公因数是（　　）

A．甲数 B．乙数 

C．1 D．甲、乙两数的积

8．若a÷b＝1……1，（a，b均是不为0的自然数），则a和b的最小公倍数是（　　）

A．1 B．a C．b D．ab

9．下面说法表述错误的是（　　）

A．假分数的分数单位都比1大 

B．等腰三角形是轴对称图形 

C．9既是奇数又是合数 

D．水价一定，总价与用水量的关系是正比例关系

10．以下说法错误的是（　　）

A．为了清楚地反映两个城市2018年月平均气温的变化情况，可以选用复式折线统计图 

B．一个三角形的面积是与它等底等高的平行四边形面积的一半 

C．0.90和0.900两个数相比，数值相等，计数单位不同 

D．将36分解质因数是36＝3×3×4

11．下列关系式，不正确的是（　　）

A．偶数+偶数＝偶数 B．合数+合数＝合数 

C．奇数+奇数＝偶数 D．质数×质数＝合数

12．1、3、7都是21的（　　）

A．因数 B．倍数 C．公因数 D．公倍数

13．42的因数中一共有（　　）个偶数。

A．2 B．4 C．6 D．8

14．李老师买了两种笔记本，价格分别为每本5元和每本2元。两种笔记本数量相同，李老师买笔记本的钱数不可能是（　　）

A．14元 B．56元 C．48元 D．63元

15．在100以内的数中，既是4的倍数，又是6的倍数的有（　　）个。

A．4 B．6 C．8 D．10

16．24和36的公因数有（　　）个。

A．3 B．4 C．5 D．6

17．一个质数和一个合数的最大公因数一定是1。要想说明上面这句话是错误的，可以用下面（　　）作为例子进行反驳。

A．3和4 B．6和8 C．2和10 D．5和7

18．如果a÷b＝5（a和b都是不为0的自然数），那么说法错误的是（　　）

A．a是合数 B．b是质数 

C．a和b的最大公因数是5 D．a和b的最小公倍数是a

二．填空题（共10小题）

19．在2、7、13、15、18这些数中，既是质数又是偶数的是 　   　，既是合数又是奇数的是 　     　。

20．在35÷7＝5中，　     　是 　      　的倍数，　      　是 　     　的因数。

21．有一个数，它既是24的因数，又是24的倍数，这个数是 　     　，它的因数中是质数的有 　      　。

22．在两位数中，同时能被3和5整除的最大奇数是 　     　。

23．在50以内，6和8的公倍数有 　        　；9和27的最大公因数是 　   　。

24．12和32的最大公因数是 　   　，最小公倍数是 　     　。

25．非0自然数a和b，如果a＝5b，那么a、b两个数的最大公因数是 　   　，最小公倍数 　   　。

26．已知x＝2y（x、y都是非零的自然数），x和y的最大公因数是 　   　，最小公倍数是 　   　。

27．哥德巴赫猜想被誉为“数学皇冠上的明珠”，内容是“任何大于2的偶数都可以表示成两个质数之和”。比如36＝　     　+　     　。

28．A＝24，B＝2×2×3×5，请把A分解质因数：　             　，A与B的最小公倍数是 　      　。

三．判断题（共10小题）

29．除2以外，任意两个质数的和都是偶数．　   　（判断对错）

30．因为9的倍数一定是3的倍数，所以3的倍数也一定是9的倍数． 　   　．

31．a（a＞1）的所有因数都小于a。 　   　（判断对错）

32．一个三位数，个位上的数字是0，并且是3的倍数，这个数一定是2、3、5的公倍数．　     　．（判断对错）

33．是一个最简分数，那么a和b的最小公倍数一定是它们的乘积。 　   　（判断对错）

34．两个自然数的最大公因数是12，这两个数的公因数有6个。 　   　（判断对错）

35．已知：a（a与b都是非0自然数，b≠0）那么a与b的最大公因数是a，最小公倍数是b。 　   　（判断对错）

36．4和10的最小公倍数是20。 　   　（判断对错）

37．非0的自然数中，不是质数就是合数．　     　．

38．把24写成质因数连乘的形式是24＝1×2×2×2×3。 　   　（判断对错）

因数和倍数的认识

参考答案与试题解析

一．选择题（共18小题）

1．4+x的和是偶数，x一定是（　　）

A．奇数 B．偶数 C．合数 D．质数

【答案】B

【分析】根据奇数、偶数的运算性质可知，偶数+偶数＝偶数，4是偶数，据此解答。

【解答】解：4+x的和是偶数，x一定是偶数。

故选：B。

【分析】本题考查了奇数、偶数的运算性质，解题的关键是知道：偶数+偶数＝偶数。

2．6的所有因数是1、2、3、6，这几个因数之间的关系是1+2+3＝6，像这样的数叫做完全数（也叫完美数）。下面的数中（　　）是完全数。

A．24 B．28 C．36 D．49

【答案】B

【分析】由题目可知，如果一个自然数等于它的全部因数（不包括本身）的和，这样的数叫“完美数“。依照“完美数”的概念，可先列举出28的所有因数，并通过求和的方法来验证。

【解答】解：因为28的因数有：1、2、4、7、14、28，这几个因数的关系是：1+2+4+7+14＝28。所以28是完美数。

故选：B。

【分析】通过题目举例，能够初步理解“完美数”的含义，运用因数的知识进行解答，其中的易错点在于相加的因数不包括这个数本身。

3．6的因数有1、2、3、6，这几个因数的关系是1+2+3＝6，像这样的数叫做完美数。下列（　　）是完美数。

A．9 B．12 C．15 D．28

【答案】D

【分析】由题目可知，如果一个自然数等于它的全部因数（不包括本身）的和，这样的数叫“完美数“。依照“完美数”的概念，可先列举出28的所有因数，并通过求和的方法来验证。

【解答】解：因为28的因数有：1、2、4、7、14、28，这几个因数的关系是：1+2+4+7+14＝28。所以28是完美数。

故选：D。

【分析】通过题目举例，能够初步理解“完美数”的含义，运用因数的知识进行解答，其中的易错点在于相加的因数不包括这个数本身。

4．下面各数中，既是6的倍数，又是54的因数的是（　　）

A．9 B．12 C．18 D．30

【答案】C

【分析】根据找一个数因数和倍数的方法，分别找出6的倍数和54的因数，然后再进行选择。

【解答】解：6×1＝6、6×2＝12、6×3＝18、6×4＝24、6×5＝30、......

6的倍数有：6、12、18、24、30、......

54＝1×54＝2×27＝3×18＝6×9

54的因数有：1、2、3、6、9、18、27、54；

因此选项A、B、C、D中既是6的倍数，又是54的因数的是18。

故选：C。

【分析】此题需要学生熟练掌握求一个数因数和倍数的方法。

5．从这四张数字卡片中任选两张，摆成不同的两位数。其中2和3的公倍数有（　　）个。

A．3 B．4 C．5

【答案】C

【分析】每张数字卡片与另外三张都可组成不同的两位数，可组成（4﹣1）×4个不同的两位数。根据2的倍数特征，2的倍数个位数字是偶数，根据3的倍数特征，一个数的各位上的数字之和是3的倍数，这个数就是3的倍数，2和3的公倍数必须同时具备2、3的倍数特征。

【解答】解：从这四张数字卡片中任选两张，摆成不同的两位数有：

12、14、15、21、24、25、42、41、45、51、51、54共12张

其中2的倍数有12、14、24、42、52、54

3的倍数有：12、15、21、24、42、45、51、54

2和3的公倍数有：12、24、42、45、54共5张

故选：C。

【分析】此题考查了简单的组合、2的倍数特征、3的倍数特征，公倍数的意义。

6．淘气买圆珠笔花了10元，笑笑买圆珠笔花了8元。如果他们买的圆珠笔的单价是一样的，那么这种圆珠笔的单价最高是（　　）元。（淘气和笑笑买圆珠笔的单价和数量都是整数）。

A．2 B．4 C．20 D．40

【答案】A

【分析】淘气买圆珠笔花了10元，笑笑买圆珠笔花了8元，因为他们买的圆珠笔的单价是一样的，所以圆珠笔的单价是10、8的公因数；求这种圆珠笔的单价最高是多少元，就是求10、8的最大公因数。

【解答】解：10＝2×5

8＝2×2×2

所以10、8的最大公因数是：2；

因此这种圆珠笔的单价最高是2元。

故选：A。

【分析】此题需要学生掌握求最大公因数的方法并灵活运用。

7．甲数是乙数的倍数，甲、乙两数的最大公因数是（　　）

A．甲数 B．乙数 

C．1 D．甲、乙两数的积

【答案】B

【分析】两个数有倍数关系时，它们的最大公约数为较小的数；由此解答问题即可．

【解答】解：因为甲数是乙数的倍数，

所以乙数是较小的数，甲数是较大的数，

所以甲和乙的最大公约数是乙；

故选：B。

【分析】此题主要考查求两个数为倍数关系时的最大公约数：两个数有倍数关系时，最大公约数为较小的数．

8．若a÷b＝1……1，（a，b均是不为0的自然数），则a和b的最小公倍数是（　　）

A．1 B．a C．b D．ab

【答案】D

【分析】由a÷b＝1……1，可知a和b是互质数，根据两个互质数的最小公倍数是两个数的乘积，据此解答。

【解答】解：若a÷b＝1……1，（a，b均是不为0的自然数），则a和b的最小公倍数是ab。

故选：D。

【分析】互质数的最大公因数是1，最小公倍数是它们的乘积。

9．下面说法表述错误的是（　　）

A．假分数的分数单位都比1大 

B．等腰三角形是轴对称图形 

C．9既是奇数又是合数 

D．水价一定，总价与用水量的关系是正比例关系

【答案】A

【分析】根据奇数与偶数、质数与合数的意义，在自然数中，是2的倍数的数叫做偶数，不是2的倍数的数叫做奇数；一个自然数，如果只有1和它本身两个因数，这样的数叫做质数，一个自然数，如果除了1和它本身还有别的因数，这样的数叫做合数。分子大于或者等于分母的分数叫假分数。把单位“1”平均分成若干份取其中的一份的数，叫做分数单位。

【解答】解：分数单位都比1小，所以假分数的分数单位都比1大表述错误；

等腰三角形的两条边相等，两个底角相等，是轴对称图形，所以等腰三角形是轴对称图形表述正确；

9既是奇数又是合数表述正确；

水价一定，总价与用水量的关系是正比例关系表述正确。

故选：A。

【分析】此题主要考查了奇数、偶数，以及质数、合数的认识，轴对称图形和正比例关系，要熟练掌握它们的特征。

10．以下说法错误的是（　　）

A．为了清楚地反映两个城市2018年月平均气温的变化情况，可以选用复式折线统计图 

B．一个三角形的面积是与它等底等高的平行四边形面积的一半 

C．0.90和0.900两个数相比，数值相等，计数单位不同 

D．将36分解质因数是36＝3×3×4

【答案】D

【分析】为了清楚地反映两个城市2018年月平均气温的变化情况，可以选用复式折线统计图；

一个三角形的面积是与它等底等高的平行四边形面积的一半；

0.90和0.900两个数相比，数值相等，计数单位分别是0.01和0.001，计数单位不同；

将36分解质因数是36＝3×3×2×2。

【解答】解：由分析知，说法错误的是D项。

故选：D。

【分析】此题考查的知识点较多，要熟练掌握。

11．下列关系式，不正确的是（　　）

A．偶数+偶数＝偶数 B．合数+合数＝合数 

C．奇数+奇数＝偶数 D．质数×质数＝合数

【答案】B

【分析】根据偶数、奇数、质数、合数的意义解答。

【解答】解：选项A中，偶数+偶数＝偶数，原题说法正确。

选项B中，如：4是合数，9是合数，4+9＝13，13是质数。原题说法错误。

选项C中，奇数+奇数＝偶数，原题说法正确。

选项D中，当两个质数相同时，质数×质数的积有3个因数，两个质数不同时，质数×质数的积有4个因数，所以质数×质数＝合数。原题说法正确。

故选：B。

【分析】此题考查了奇数和偶数、质数和合数的性质。

12．1、3、7都是21的（　　）

A．因数 B．倍数 C．公因数 D．公倍数

【答案】A

【分析】如果整数a能被整数b整除（b≠0），a就叫做b的倍数，b就叫做a的因数。

【解答】解：21÷1＝21，21÷3＝7，21÷7＝3，所以1、3、7都是21的因数。

故选：A。

【分析】此题需要学生掌握因数和倍数的意义。

13．42的因数中一共有（　　）个偶数。

A．2 B．4 C．6 D．8

【答案】B

【分析】先找出42的所有因数有：1、2、3、6、7、12、21、42，然后再观察因数有几个偶数即可。

【解答】解：42＝1×42＝2×21＝3×14＝6×7

所以42的因为有：1、2、3、6、7、12、21、42，其中偶数有4个。

故选：B。

【分析】本题要求学生掌握找一个数的因数的方法并灵活运用。

14．李老师买了两种笔记本，价格分别为每本5元和每本2元。两种笔记本数量相同，李老师买笔记本的钱数不可能是（　　）

A．14元 B．56元 C．48元 D．63元

【答案】C

【分析】根据两种笔记本的价格为5元和2元，因为数量相同，所以总钱数一定是（5+2）的倍数。只要找出选项中不是（5+2）的倍数的数即可。

【解答】解：5+2＝7

A选项14÷7＝2，是7的2倍，不符合题意。

B选项56÷7＝8，是7的8倍，不符合题意。

C选项48÷7＝6……6，不是7倍数，符合题意。

D选项63÷7＝9，是7的9倍，不符合题意。

故选：C。

【分析】本题考查7的倍数的特征，掌握7的乘法口诀是解决本题的关键。

15．在100以内的数中，既是4的倍数，又是6的倍数的有（　　）个。

A．4 B．6 C．8 D．10

【答案】C

【分析】先求出4和6的最小公倍数，再一次扩大2倍、3倍、4倍……直到倍数接近100而小于100，数出一共有几个即可。

【解答】解：4和6的最小公倍数是12

12×2＝24

12×3＝36

12×4＝48

12×5＝60

12×6＝72

12×7＝84

12×8＝96

在100以内的数中，既是4的倍数，又是6的倍数的有8个。

故选：C。

【分析】本题考查公倍数和最小公倍数的计算。掌握求最小公倍数的方法是解决本题的关键。

16．24和36的公因数有（　　）个。

A．3 B．4 C．5 D．6

【答案】D

【分析】先分别找出24和36的因数，然后再找出它们的公因数。

【解答】解：24的因数有：1、2、3、4、6、8、12、24；

36的因数有：1、2、3、4、6、9、12、18、36；

24和36的公因数有：1、2、3、4、6、12；共6个。

故选：D。

【分析】此题需要学生熟练掌握求一个数因数的方法，以及求两个数公因数的方法。

17．一个质数和一个合数的最大公因数一定是1。要想说明上面这句话是错误的，可以用下面（　　）作为例子进行反驳。

A．3和4 B．6和8 C．2和10 D．5和7

【答案】C

【分析】根据质数与合数的概念，在选项中找出一个质数和一个合数的选项，求出它们的最大公因数即可解答。

【解答】解：一个质数和一个合数的项是C，因为2和10为倍数关系，所以2和10的最大公因数是2，不是1；其它选项不是两个质数就是两个合数。

故选：C。

【分析】熟练掌握合数与质数的意义以及为倍数关系的两个数的最大公因数的求法是解题的关键。

18．如果a÷b＝5（a和b都是不为0的自然数），那么说法错误的是（　　）

A．a是合数 B．b是质数 

C．a和b的最大公因数是5 D．a和b的最小公倍数是a

【答案】B

【分析】如果a÷b＝5（a和b都是不为0的自然数），那么a和b有因数和倍数的关系，则b、5都是a的因数；不一定是质数，可举例说明；为倍数关系的两个数的最大公因数是较小的数，最小公倍数是较大的数。

【解答】解：因为a÷b＝5（a和b都是不为0的自然数）

所以a的因数有1、b、5、a，所以a是合数；

b不一定是质数，例如20÷4＝5，4是合数，所以b是质数的说法错误；

因为a÷b＝5（a和b都是不为0的自然数），所以a和b的最大公因数是5，最小公倍数是a。

故选：B。

【分析】熟练掌握因数与倍数的关系，质数与合数的特征以及为倍数关系的两个数的最大公因数和最小公倍数的求法是解题的关键。

二．填空题（共10小题）

19．在2、7、13、15、18这些数中，既是质数又是偶数的是 　2　，既是合数又是奇数的是 　15　。

【答案】2，15。

【分析】根据质数和合数、偶数和奇数的定义即可解答。

【解答】解：在2、7、13、15、18中，质数有：2、7、13，偶数有：2，18，既是质数又是偶数的是2；合数有15，18，奇数有7，13，15，既是合数又是奇数的是15。

故答案为：2，15。

【分析】解答此题重点在于能分清质数和合数、偶数和奇数。

20．在35÷7＝5中，　35　是 　5和7　的倍数，　5和7　是 　35　的因数。

【答案】35，5、7；5、7，35。

【分析】若整数a能够被b整除，a叫做b的倍数，b就叫做a的因数，因数与倍数是相互依存的，据此解答。

【解答】解：在35+7＝5中，35是5和7的倍数，5和7是35的因数。

故答案为：35，5、7；5、7，35。

【分析】本题主要考查因数与倍数的意义，注意因数与倍数是相互依存的。

21．有一个数，它既是24的因数，又是24的倍数，这个数是 　24　，它的因数中是质数的有 　2、3　。

【答案】24，2、3。

【分析】因为一个数的最大因数和最小倍数都是它本身，所以根据“一个数，它既是24的因数，又是24的倍数”，可知这个数就是24；再把24分解质因数，即可得出结论。

【解答】解：有一个数，它既是24的因数，又是24的倍数，这个数是24，它的因数中是质数的有2、3。

故答案为：24，2、3。

【分析】此题考查因数与倍数的意义，利用一个数的倍数最小是它的本身，一个数的约数最大也是它本身，解决问题；也考查了合数分解质因数的方法．

22．在两位数中，同时能被3和5整除的最大奇数是 　75　。

【答案】见试题解答内容

【分析】先求出3和5的最小公倍数，然后再用最小公倍数乘奇数，就得到3和5的奇数倍，找出两位数中最大的一个即可。

【解答】解：3和5的最小公倍数是15，

15×3＝45，15×5＝75，15×7＝105，

所以能同时被3和5整除的两位数，如果是奇数，最大是75；

故答案为：75。

【分析】解答本题关键是先找出3和5的最小公倍数，然后再用最小公倍数乘奇数，就得到3和5的奇数倍。

23．在50以内，6和8的公倍数有 　24、48　；9和27的最大公因数是 　9　。

【答案】24、48；9。

【分析】公倍数是两个数公有的倍数，先找出两个数的倍数，从中找出公有的倍数；

公因数是两个数公有的因数，先求出两个数的因数，然后找出公有的因数即可，公因数中最大的一个就是这两个数的最大公因数，据此找出9和27的最大公因数。

【解答】解：50以内6和8的倍数是：

6的倍数是：6、12、18、24、30、36、42、48，

8的倍数是：8、16、24、32、40、48，

50以内6和8的公倍数有：24、48；

9的因数有：1、3、9，

27的因数有：1、3、9、27，

9和27的公因数有：1、3、9；9和27的公因数1、3、9中，9是最大的，所以9和27的最大公因数是9。

故答案为：24、48；9。

【分析】此题需要学生掌握倍数，公倍数，因数、公因数和最大公因数。

24．12和32的最大公因数是 　4　，最小公倍数是 　96　。

【答案】4；96。

【分析】对于一般的两个数来说，这两个数的公有质因数的连乘积是这两个数的最大公因数，这两个数的公有质因数与每个数独有质因数的连乘积是最小公倍数；当两个数成倍数关系，最大公因数为较小的数，较大的那个数，是这两个数的最小公倍数；是互质数的两个数，它们的最大公因数是1，最小公倍数即这两个数的乘积。

【解答】解：12＝2×2×3

32＝2×2×2×2×2

最大公因数是：2×2＝4

最小公倍数是：2×2×3×2×2×2＝96

故答案为：4；96。

【分析】熟练掌握两个数的最大公因数和最小公倍数的求法是解题关键。

25．非0自然数a和b，如果a＝5b，那么a、b两个数的最大公因数是 　b　，最小公倍数 　a　。

【答案】b，a。

【分析】两个数为倍数关系，则最大公因数是较小的数，最小公倍数为较大的数。

【解答】解：因为a＝5b，所以a÷b＝5，所以a、b两个数的最大公因数是b，最小公倍数a。

故答案为：b，a。

【分析】考查了求几个数的最大公因数的方法与最小公倍数的方法：两个数为倍数关系，则最大公因数是较小的数，最小公倍数为较大的数。

26．已知x＝2y（x、y都是非零的自然数），x和y的最大公因数是 　y　，最小公倍数是 　x　。

【答案】y；x。

【分析】两个数为倍数关系，则最大公因数是较小的数，最小公倍数为较大的数。

【解答】解：因为x÷y＝2（x、y都是非零的自然数），所以x和y的最大公因数是y，最小公倍数是x。

故答案为：y；x。

【分析】明确为倍数关系的两个数的最大公因数是较小的数，最小公倍数为较大的数是解题的关键。

27．哥德巴赫猜想被誉为“数学皇冠上的明珠”，内容是“任何大于2的偶数都可以表示成两个质数之和”。比如36＝　13　+　23　。

【答案】5、31或7、29或13、23或17、19。

【分析】40以内的质数从小到大依次排列为：2、3、5、7、11、13、17、19、23、29、31、37，36是两个质数之和，其中一个质数不可能是2，所以依次往后试一试。

【解答】解：36＝5+31

36＝7+29

36＝13+23

36＝17+19

故答案为：5、31或7、29或13、23或17、19。

【分析】此题主要考查了质数的定义，熟练掌握100以内的质数是关键。

28．A＝24，B＝2×2×3×5，请把A分解质因数：　24＝2×2×2×3　，A与B的最小公倍数是 　120　。

【答案】24＝2×2×2×3；120。

【分析】根据分解质因数的方法，将24分解质因数，并将其和B共有的质因数和独有的质因数相乘，求出A和B的最小公倍数。

【解答】解：A＝24＝2×2×2×3

B＝2×2×3×5

2×2×3×2×5＝120

所以，把A分解质因数为：24＝2×2×2×3，A与B的最小公倍数是120。

故答案为：24＝2×2×2×3；120。

【分析】本题考查了最小公倍数。求两个数的最小公倍数，先分解质因数，再将两数共有的和独有的质因数连乘求出乘积即可。

三．判断题（共10小题）

29．除2以外，任意两个质数的和都是偶数．　√　（判断对错）

【答案】见试题解答内容

【分析】不是2的倍数的数叫做奇数，一个数只有1和它本身两个因数，这个数叫作质数，质数除了2以外都是奇数，根据奇数+奇数＝偶数，解答判断即可．

【解答】解：2是偶数，也是奇数，最小的质数2，质数除了2以外都是奇数，奇数+奇数＝偶数，

所以“除了2以外的任意两个素数的和都是偶数”的说法是正确的．

故答案为：√．

【分析】此题主要明白质数除了2以外都是奇数，奇数+奇数＝偶数．

30．因为9的倍数一定是3的倍数，所以3的倍数也一定是9的倍数． 　×　．

【答案】×

【分析】采用特殊值法，6是3的倍数，但是6不是9的倍数．

【解答】解：由以上分析，9的倍数一定是3的倍数，但3的倍数不一定是9的倍数．

故答案为：×．

【分析】此题主要考查了倍数的意义．

31．a（a＞1）的所有因数都小于a。 　×　（判断对错）

【答案】×

【分析】一个数的因数的个数是有限的，其中最小的因数是1，最大的因数是它本身，据此进行判断。

【解答】解：例如：整数6的因数有1，2，3，6；其中6是最大的因数，就是6本身；

整数10的因数有1，2，5，10；其中10是最大的因数，就是10本身；

所以说一个数的因数一定不大于这个数。

故答案为：×。

【分析】此题要求学生熟练掌握求一个数因数的方法。

32．一个三位数，个位上的数字是0，并且是3的倍数，这个数一定是2、3、5的公倍数．　√　．（判断对错）

【答案】见试题解答内容

【分析】根据2、3、5的倍数特征可知：个位上是0的数能同时被是2和5倍数，此题这个数是3的倍数已知，据此分析解答．

【解答】解：个位上是0的数能同时被是2和5倍数，此题这个三位数是3的倍数已知，所以一个三位数，个位上的数字是0，并且是3的倍数，这个数一定是2、3、5的公倍数的说法是正确的；

故答案为：√．

【分析】本题主要考查2、3、5的倍数特征，注意个位上是0的数能同时被是2和5倍数．

33．是一个最简分数，那么a和b的最小公倍数一定是它们的乘积。 　√　（判断对错）

【答案】√

【分析】最简分数就是不能约分的分数，分子和分母只有公因数1，也就是互质数。那么a和b的最小公倍数就一定是它们的乘积。

【解答】解：是一个最简分数，那么a和b的最小公倍数一定是它们的乘积。√（判断对错）

故答案为：√。

【分析】本题的关键是最简分数的概念，以及互质数的最小公倍数的计算方法。

34．两个自然数的最大公因数是12，这两个数的公因数有6个。 　√　（判断对错）

【答案】√

【分析】这两个自然数的公因数就是它们最大公因数的因数；因为12的因数有1、2、3、4、6、12 共6个；所以这两个自然数的公因数有6个，即1、2、3、4、6、12；据此解答即可。

【解答】解：因为12的因数有1、2、3、4、6、12 共6个；

所以这两个自然数的公因数有6个，即1、2、3、4、6、12，故原题说法正确。

故答案为：√。

【分析】解答此题应根据找一个数的因数的方法进行解答；应明确：两个自然数的公因数就是它们最大公因数的因数。

35．已知：a（a与b都是非0自然数，b≠0）那么a与b的最大公因数是a，最小公倍数是b。 　√　（判断对错）

【答案】√

【分析】因为a，所以b÷a＝5，而a与b都是非0自然数，当两个数为倍数关系，则最大公因数是较小的数，最小公倍数为较大的数。

【解答】解：根据分析，因为a，所以b÷a＝5，而a与b都是非0自然数，所以a与b的最大公因数是a，最小公倍数是b，因此原题说法正确。

故答案为：√。

【分析】此题需要学生熟练掌握求两个数的最大公因数和最小公倍数的方法。

36．4和10的最小公倍数是20。 　√　（判断对错）

【答案】√

【分析】先把4和10进行分解质因数，这两个数的最小公倍数是这两个数的公有质因数与独有质因数的连乘积，由此解决问题即可。

【解答】解：4＝2×2，10＝2×5，

所以4和10的最小公倍数是2×2×5＝20

所以题干说法正确。

故答案为：√。

【分析】对于一般的两个数来说，这两个数的公有质因数的连乘积是这两个数的最大公因数；是互质数的两个数，它们的最大公因数是1，最小公倍数即这两个数的乘积。

37．非0的自然数中，不是质数就是合数．　×　．

【答案】见试题解答内容

【分析】找出非0的自然数中，有既不是质数又不是合数的数就可以证明，问题得解．

【解答】解：1既不是质数又不是合数，

所以非0的自然数中，不是质数就是合数的说法是错误的；

故答案为：×．

【分析】本题主要考查质数与合数的意义．

38．把24写成质因数连乘的形式是24＝1×2×2×2×3。 　×　（判断对错）

【答案】×

【分析】根据合数分解质因数的意义判断即可。

【解答】解：把24写成质因数连乘的形式是24＝2×2×2×3，所以原题说法错误。

故答案为：×。

【分析】本题主要考查分解质因数的应用。